【振動】便利な換算方法
皆さんこんにちは。振動くんの独り言の投稿です。
本日は、振動の測定パラメータである加速度、速度、変位の変換方法について記載したいと思います。
振動は目に見えなくても、グラフ上で換算ができる
振動は一見、目に見えないので難しいと感じている方が多いようですが、実はそんなに難しく感じる必要はなく、1つの測定パラメータ(例えば「加速度」)とその周波数が解かっていれば、他の測定パラメータである「速度」と「変位」は計算で求めることが出来ます。
振動諸元換算表(トリパタイトグラフ)の存在
振動の換算を簡単に行える換算表があります。この換算表のことをトリパタイトグラフと呼びます。

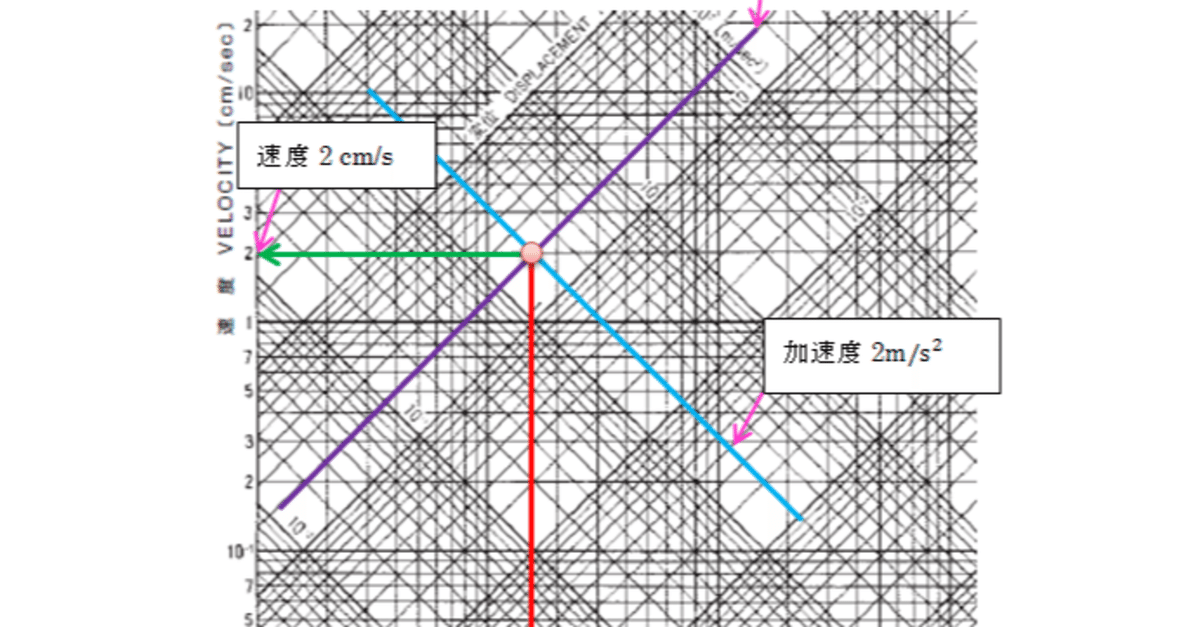
このグラフの特徴は、横軸が周波数、縦軸が速度になっており、左下から右上に対して加速度、右下から左上に対して変位が目盛られています。目盛りは全て対数目盛です。なんだか頭痛がしそうなグラフですね。
トリパタイトグラフの見方

横軸は周波数、単位はHz(ヘルツ)です。
Y軸(緑の矢印)は、速度で単位はcm/sです。
右上に対して目盛られた軸(青の矢印)は、加速度で単位はm/s^2です。
左上に対して目盛られた軸(紫の矢印)は、変位で単位はmmです。
トリパタイトグラフの使い方
トリパタイトグラフを使う時には、振動測定パラメータの1つとその周波数が解かっている必要があります。
変位をD(単位:m)とすると
速度V(単位:m/s)は、 V=ω×D=2πf×D (1)
加速度A(単位:m/s^2)は、 A= ω×V=ω^2×D=((2πf))^2×D (2)
ここで、fは周波数(Hz)を表します。単位に注意して下さい。
上記の内容を詳しく知りたい方は、以下を参照して下さい。
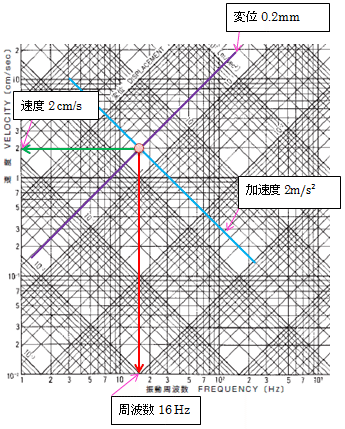
上のグラフの赤丸の部分の加速度、速度、変位を求めてみましょう。
上のグラフで赤丸の部分は、周波数16Hz、速度2cm/sの場所です。
よって、加速度A(m/s^2)は、(2)式を用いて
A=0.02 (m/s)×2×π×16(Hz) =2.00 (m/s^2) となります。
また、 変位D(m)は、(1)式を用いて
D=V/(2πf)=0.02(m/s)/( 2×π×16)=0.0001999 m=0.2 mm
グラフの赤丸部分の交点は、上記の加速度と変位の計算結果と一致していることが解ります。如何ですか? 簡単に求めることが出きましたね。
上記の計算は、振動の周波数が1つの場合(単一振動)に適用されます。
実際の加速度振動は様々な周波数を持った加速度の集まりです。
従って、FFT解析で出てきた加速度振幅の大きい上位5個位の周波数に対して変換(速度または変位)を行い、和を取れば値を特定(計算)することが出来ます。
これから先は輸送振動試験に関する投稿です。トリパタイトを使って振動試験機が使えるかどうかの判断の仕方等を投稿しています。
通常の投稿は以上です。閲覧頂きありがとうございます。
次回の投稿をご期待下さい。
この記事が気に入ったらチップで応援してみませんか?

