【スマホでPython数学】 第3章 因数分解と式の展開

前の章ではSympyモジュールの導入と高次関数の因数分解を学びました。この章では因数分解の逆、式の展開についてPythonを使ってやってみましょう。

1．式の展開：expand（エキスパンド）命令

因数分解では、高次関数を１次式などの積（かけ算）の形で表しました。今度は、１次式などの積（かけ算）の形を展開して、高次関数に直します。学校の数学では、２通りのやり方が紹介されています。一つは、１つの変数や定数毎に展開をしていくやり方です。もう一つは、公式を使った展開の仕方になります。この辺りも興味があれば、教科書やインターネットで見てみてください。
Pythonでのプログラムは簡単です。前の章のfactor（ファクター）命令をexpandに換えるだけです。今度はexpand命令の中にある式を因数分解の時のように低次関数の積（かけ算）の形にする必要があります。

from sympy import *
var('x')

ここまではいつもの「おまじない」です。
Sympyモジュールを導入して、変数$${x}$$を定義します。
次に、expand命令を使ってみます。

expand((x-2)*(x-3))

expand命令の中は（カッコ）でくくります。それでは、このプログラムを実行してみてください。

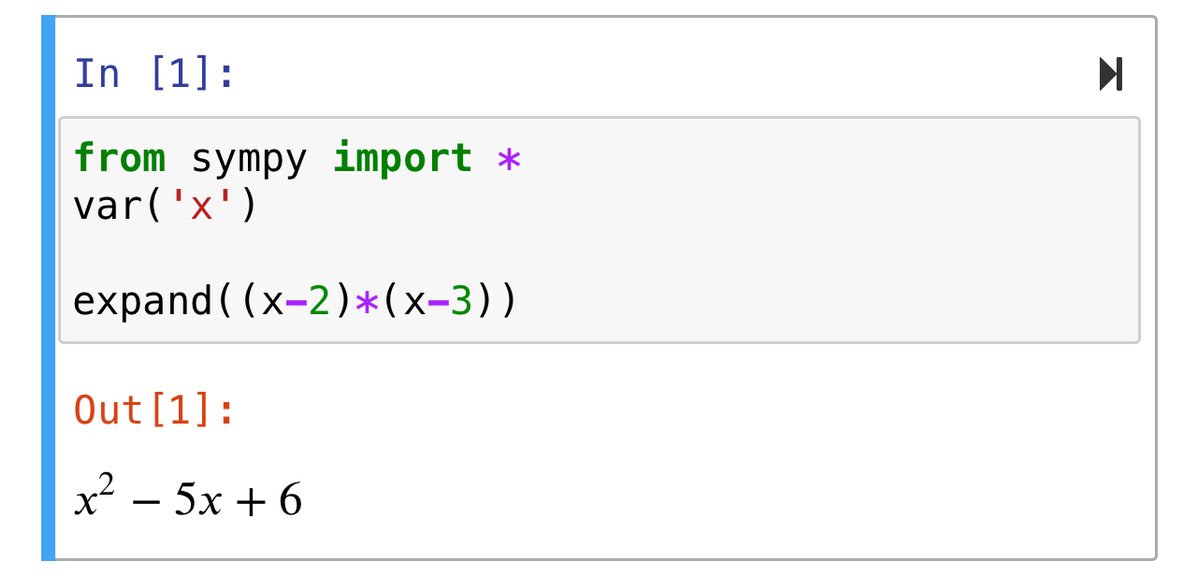
いかがだったでしょうか？上のように出力（Out[ ]）されたでしょうか？カッコが閉じていないとエラーが出ますので、ご注意ください。（エラーが出たら直して、再度実行するだけなので、たくさん間違っていただいて大丈夫です！）

2．もう少し高次な式の展開

それではこの勢いで、さらに高次な関数の式の展開をしてみましょう。原理的には何次式でも展開は可能ですので、いろいろやってみます。
まずは、三次関数。

expand((x-2)*(x-3)*(x-4))

次に、四次関数の展開をしてみます。

expand((x-1)*(x-2)*(x-3)*(x-4))

いかがだったでしょうか？
それぞれ、以下のような結果が得られたでしょうか？

3．因数分解と式の展開の関係

もうお気づきだと思いますが、因数分解と式の展開は、表と裏の関係にあり（どちらが表とか裏とかはないのですが…）、著者も第2章での因数分解の際には、まず式の展開をしてから問題を作成していました。きれいに因数分解できる式を作るのは意外と大変なのです（笑）。それでは、先ほどの最後の問題で展開した四次関数を因数分解してみましょう。

演習１：$${x^4 - 10x^3 + 35x^2 - 50x + 24}$$

from sympy import *
var('x')
faｃtor(x**4 -10*x**3 +35*x**2 -50*x +24)

どうでしょうか？きれいな形に因数分解できたでしょうか？
それでは、残り2つの演習で、式の展開をしてみてください。

演習２：$${(x - 5)(x + 4)(x - 3)}$$

expand((x - 5)*(x + 4)*(x -3))

演習３：$${(2x - 1)(x - 6)(5x + 1}$$

expand((2*x -1)*(x - 6)*(5*x +1))

4．計算結果を引き継ぐ記号：「_（アンダースコア）」

Jupyter上で計算結果などを引き継ぐ記号として、「_（アンダースコア）」があります。−（マイナス）記号ではなく、下線のように下の方にある「_」という記号になります。キーボードのどこにあるか探してみてください。必ずあるはずです。
演習の2と3で行った展開の際に、展開後の高次式をもう一度因数分解してみます。expand命令で式を展開した後に「factor(_)」とすると、直前の結果を引き継いで、直前の結果に対してfactor命令が実行されます、

これはJupyterの便利な機能ですので、覚えておいてください。自分で展開した後に、「factor(_)」としてみると面白いです。

まとめ

やっと、コンピュータを使った方が簡単そう、という段階になってきました。次の章では「関数」と「方程式」について勉強したいと思います。

解答