因果探索の数理に入門してみた

2023年12月14日 17:55

※本記事は統計・機械学習の数理 Advent Calendar 2023 14日目の記事として掲載しております。統計・機械学習の数学に関する様々な記事が掲載されていますので、ぜひご覧ください。

はじめに

早いもので2023年も終わろうかという今日この頃ですが、私にとって今年のテーマの1つであった「因果探索」についてその数理的側面に入門してみたいと思います。

Introduction

なぜ因果探索なのか

「因果推論」というより馴染み深い似た言葉がありますが、今回の「因果探索」は因果推論に包含されるトピックになります。因果推論というとRubin流・Pearl流という2つの主要な枠組みがありますが、後者にあたるPearl流の枠組みにおいて「構造的因果モデル(Structural Causal Model: SCM)」が因果推論の道具になるため、SCMを構成する因果グラフの構造を推定するための理論的枠組みとして因果探索というトピックが存在しているという整理になるでしょう。
因果探索の推定対象となる因果グラフは以下のように変数間の因果関係を矢印によって描いており、これによって変数間の関係を可視化することができます。
Pearl氏はその著書『The Book of Why: The New Science of Cause and Effect』の中で、この因果グラフを用いることで条件付き確率-介入-反事実という3段階（彼はこれを「因果のはしご」と呼んでいますが）の因果推論全てにアプローチすることができると述べており、因果グラフが不可欠なツールであることを示唆しています（*1）。

さて、そんな因果グラフを活用して因果推論を行うためには、因果グラフ自体を手元に用意する必要があります。その手段としては2つに一つで、仮説をもとに自分で用意するかデータから推定するかのどちらかになります。しかし、対象とする項目が多かったり、構造が複雑だったりすると、仮説ベースで因果グラフを描き切ることは難しいでしょう。このように因果グラフが未知の状況で、データから因果グラフを推定することが因果探索のモチベーションになります。

因果探索の基本問題

イントロダクションが長くなっていますが、ここからは因果グラフを数理的に表し、因果探索の論点に迫っていきます。図1のような変数で構成される現象があると仮定します。

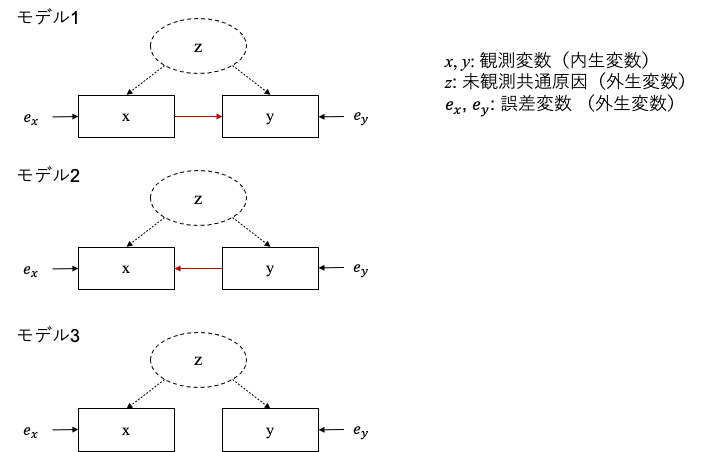
これらの変数の関係性にはいくつかの候補があり、それぞれ次のような構造方程式で表すことができます。

$$
モデルA :
\begin{cases}{}
x = f_x(z, e_x)\\
y= f_y(x,z,e_y)\\
p(z,e_x,e_y) = p(z)p(e_x)p(e_y)
\end{cases} \thinspace
モデルB :
\begin{cases}{}
x_1 = e_1\\
x_2 =f_2(x_1, e_2)\\
x_3 = f_3(x_1, e_3)
\end{cases} \thinspace
モデルC:
\begin{cases}{}
x = f_x(z, e_x)\\
y= f_y(z,e_y)\\
p(z,e_x,e_y) = p(z)p(e_x)p(e_y)
\end{cases}
$$

$${x}$$, $${y}$$ などの観測変数（内生変数といったりもします）はそれぞれ、観測誤差や未観測の原因（図1$${z}$$ のように観測できないが $${x, y}$$ の交絡となりうる変数）といった外生変数と合わせて関数形 $${f_x, f_y}$$ の入力となり、これらを組み合わせて各変数のデータ生成過程を定義します。
上記の候補たちは、各変数のデータ生成過程のパターンで考えられる組み合わせを表したものであり、このうち真のデータ生成過程を示すものがどれなのかを推定することが因果探索の基本問題ということになります。

因果グラフ推定の数理

前項で定義してきた因果探索の基本問題をもとに、もとの因果グラフを推定するアプローチについて解説していきます。我々がデータに基づいてもとの因果グラフを推定する際、一般に以下の観点に基づいたアプローチで推定することを考えていきます。

観測変数の関数形 $${f_x}$$ と $${f_y}$$ にどのような仮定をおくのか
外生変数 $${z}$$, $${e_x}$$, $${e_y}$$ の分布 $${p(z)}$$, $${p(e_x)}$$, $${p(e_y)}$$ にどのような仮定をおくのか

これらに加えて、因果グラフの推定にあたりいくつかの重要な概念について紹介しておきます。

識別性

ここで、本記事で最も重要なポイントである因果グラフの識別性について解説しておきましょう。因果探索において、因果グラフが識別可能であるということは、もとの因果グラフを復元できることを意味しており、因果グラフの識別は因果グラフの構造が異なる場合に観測変数の分布が必ず異なるという性質に基づいてなされるとされます。つまり、因果探索の基本的なアプローチは、データ生成過程の構成要素（観測変数や誤差項など）に仮定をおいたりおかなかったりして、それによって考えられるデータ生成過程のパターンにおける観測変数の分布が異なる構造をもとの因果グラフとすることができるということです。

実はこれから述べる推定のアプローチには、それぞれ置かれた仮定の違いにより、因果グラフが識別可能かどうかが異なります。識別できないアプローチは因果探索の問題を直接解決することはできませんが、因果探索においてどんな条件で因果関係を定義できるのかを比較によって明らかにするという観点で検討しておいて損はないでしょう。

因果的マルコフ条件

観測変数間の条件付き独立性に基づく推測原理で、「変数それぞれが、その親にあたる変数で条件づけると、その非子孫の変数と独立になる」という条件です。式で書くと、以下が成り立つことを表します。

$${p(x) = \prod_{i=1}^p p(x_i | pa(x_i))}$$

もう少し詳しく見ていきましょう。3つの観測変数 $${x_1, x_2, x_3}$$ に以下のような因果構造が仮定できるとします。

このグラフにおいて、因果的マルコフ条件を用いると、 $${x_2}$$ は、その親である $${x_1}$$ で条件づけると、$${x_1}$$ の非子孫である $${x_3}$$ と独立であることが成り立ちます。加えて、「条件付き独立性は、因果的マルコフ条件から導かれるもののみである」という忠実性を仮定できることで、因果的マルコフ条件が因果グラフを推定するためのアプローチの一部となります。

因果グラフの推定アプローチ

ではここから、簡単のため未観測共通原因がなく、因果関係が非巡回で、関数 $${f_x, f_y}$$ が線形という仮定のもとで、3つのアプローチの概要とそれぞれの識別性を比較します。
ここでは、以下のような因果グラフをもとの因果グラフと考えるとしましょう。先ほどの3つの観測変数 $${x_1, x_2, x_3}$$ があり、それらの因果グラフは未知であるとします。

アプローチ1
- 観測変数の関数形、外生変数の分布のいずれにも仮定をおかない（ノンパラメトリック）アプローチになります。従って、両者に仮定を置かずとも使える因果的マルコフ条件（および忠実性）にもとづいて因果グラフを推定していきます。
  上記のような未知であるもとのデータ生成過程から抽出された変数 $${x_1, x_2, x_3}$$ がある状態で、我々は変数間に存在する条件付き独立性を考えることができます。それにより、例えば「$${x_1}$$ を所与とした $$x_2$$ と $${x_3}$$ の条件付き独立性」が判明することで、図4のような同値類と呼ばれるグラフの候補が特定できるわけです。しかし、そこから因果の方向を推定することはできず、探索を終了せざるを得ないわけです。

アプローチ2
- 観測変数の関数形に仮定をおくことを基本としたアプローチになります。最も一般的なものは、観測変数の関数形が線形であるという仮定です。
  変数 $${x_1, x_2}$$ の2つで構成される因果グラフを別途導入します。構造方程式はそれぞれ以下のパターンを仮定することができ、。

$$
モデル1 :
\begin{cases}{}
x_1 = f_1(x_2, e_1)\\
x_2 = e_2
\end{cases}
$$

$$
モデル2:
\begin{cases}{}
x_1 = e_1\\
x_2 = f_2(x_1, e_2)
\end{cases}
$$

※関数 $${f_1, f_2}$$ は線形関数

$${x_1, x_2}$$ の構造は、両モデルを通じて以下のパターンになります。

$${x_1 = \begin{cases}{} f_1(x_2, e_1)\\ e_1 \end{cases} x_2 = \begin{cases}{} f_2(x_1, e_2) \\ e_2 \end{cases}}$$

ここで、誤差変数の分布について考えてみましょう。
まず、誤差変数にも同様に仮定をおく（＝ガウス分布に従う）とします。すると、再生性により観測変数と誤差変数の線形和はガウス分布に従うため、変数 $${x_1, x_2}$$ は上記のいずれであってもガウス分布に従います。この時、分布の形が同じになる場合があるため、必ずしも因果グラフを識別することはできません。

従って、誤差変数には仮定をおかず（＝何らかの非ガウス分布に従う）、観測変数の分布の違いを利用して一意な因果グラフを識別することになります。この時、引き続き観測変数の関数形に線形という仮定をおいた場合にはLiNGAMというモデルを使って一意な因果グラフを推定することができます。一方で、関数形が非線形である場合のアプローチについても研究が展開されています。（*2）

終わりに

今回は、統計的因果探索という領域への入門として、因果関係をどのように定義できるのかを数理的に解説してみました。まとめると、

因果的マルコフ条件（条件付き独立性に基づく原理）により変数間の従属関係を特定する
観測変数の分布の形の違いにより、因果構造を推定できる

ということになるかと思います。（*3）
現時点では、今回取り上げた以外にも前提条件（*4）にもとづいて因果グラフを推定していくため、実態との乖離がある程度発生しうるという認識ではありますが、例えばマーケティング活動の全体像を効率的に可視化してくれることでそこで作られた因果グラフをもとに仮説を洗練させつつ効果的な検証を行うなど一定の貢献度があるのではないかと思っています。

今回の内容は、因果探索の基本問題の範囲を出ていないベーシックな概念の解説に終始していると認識していますが、整理していて未だにしっくりきていないのは、パラメトリックな（観測変数の関数形&誤差変数の両方にガウス分布に従うという仮定をおく）場合に因果グラフを識別できないロジックについてです。再生性が成り立つことは分かりますが、誤差変数は平均0の分散1を仮定し、さらに観測変数を線形結合した係数がイコールで向きが違うという特殊な状況下において識別性を失ってしまうと認識していますが、もしも違っていましたら教えてください🙇‍♂️🙏

とりあえず今回はここまで。次回は、観測変数に線形の仮定をおいたモデルとしてLiNGAMの数理について整理してみたいと思います！

*1 : ちなみに因果のはしごに関する概念的な整理について別の記事で言及していますので、ご興味あればチェックしてみてください↓

*2 : 今回は入門ということ~~にして~~で、あまり深追いはしません🙇
*3 : 非線形に関しても、識別性の入り口は分布の形の違いをもとにしているようです（Hoyer et al., 2009）。
*4: 因果グラフは有向（≒矢印に向きがある）で非巡回（ある変数から同じ変数に戻ってこない≒閉路がない）

参考文献

Judea Pearl, Dana Mackenzie. 2018, 『The Book of Why: The New Science of Cause and Effect』, Basic Books
清水昌平, 2017, 『統計的因果探索』, 講談社サイエンティフィク
Patrik Hoyer, Dominik Janzing, Joris M. Mooij, Jonas Peters & Bernhard Schölkopf., 2009, Nonlinear causal discovery with additive noise models. In Advances in Neural Information Processing Systems 21 (NIPS)