
無難な道を選び続けるとどうなるのだろうか?
財布の中に入っている100円玉を見てふとそんなことを思ったので今日はそれをテーマに書いてみようと思う。
なぜそんなことが思い浮かんだかというと、以前本当に確率は収束するのか100円玉を1万回トスしたことがあるからだ。
その記録をスプレットシートにまとめたものはこんな感じである。

もちろんただ目的もなくそんなことをする訳もなく、株などでどうやったら稼ぐことができるかの研究の一環だった。
その結果を図にしたものはこんな感じだ。

この1:1というのは100円の表が出ると1、裏が出ると-1として記録していったことを示してる。
結果は見ての通り、約5,000回を超えるまでひたすら負けているのである。
100円の表と裏の出る確率は50%なのにである。
(もちろん重さや汚れで若干の偏りはある)
この偏りは逆正弦法則と呼ばれるもので、勝ち続ける人は勝ち続けて、負け続ける人は負け続けると言いうものである。
これを我々の生活に当てはめて、無難な道を選び続けるとする。
無難な道を選び続けるとスキルや経験の幅が狭まり、成長できずに失敗の連続に陥る可能性がある。
つまり無難な道を選んで得られるものを1、失敗した場合を-1とした場合、無難な道を選び続けてもいい方向に進まないこともあるということだ。
では挑戦し続けた場合はどうだろうか?
もちろん失敗もあるが挑戦したことによって経験値が増え、成長につながる可能性がある。
でも仮に人並みに頑張って得られるものが1とし、失敗したら-1とすると、こちらもいい方向に進むまでにかなりの時間を要す可能性がある。
じゃあ人より少しだけ頑張ればどうだろうか?
例えば、出社前の毎日30分だけ英語の勉強をして海外のお客さんとやり取りを行うなどとする。
これを人より1.5倍頑張ったと仮定し、得られるものを1.5、失敗した時は-1となるとしよう。
そうすると結果はこうなる。
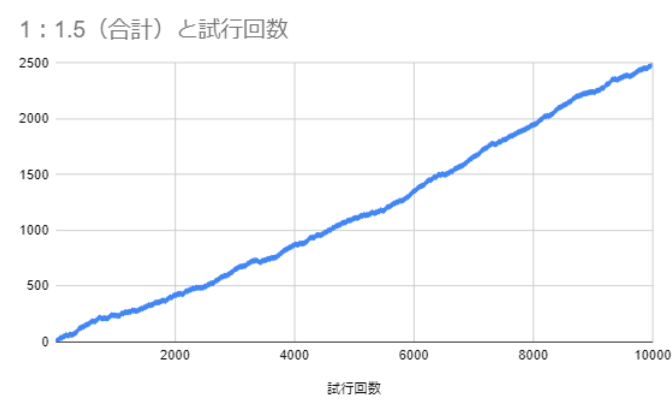
これはあくまでも失敗のシビアさは同じという前提があるから成り立つが、失敗をしたとしても得るものの方が大きくなる。
ちなみに人の2倍頑張った場合はこんな感じだ。

人より1.5倍頑張る人より最終的に倍の結果を得ている。
人の2倍頑張るのは難しい。
難しいがゆえに、得られるものも当然大きい。
でももしかしたら人よりちょっと、1.5倍頑張るのであればできるかもしれない。
人より1.5倍だけ頑張ってみる。
そうすると少し変わった結果を得られるかもしれない。
そんなことを財布の中の100円を見てふと思った一日だった。
