Newton力学⑥ 仕事と力積

前回の記事はこちら↓

必要な前提知識はこちら↓
・極限と微分，積分(準備中……)
・ベクトル，行列とベクトル解析(準備中……)

Newton力学の６回目です。
今回は，力を別の角度から見直してみます。
大雑把に言うと，「最初の方でお話しした”運動エネルギー”と”運動量”を活用しよう！」というお話です。

つまり，「運動している物体がある」のではなく，「運動エネルギーと運動量がある」と捉えなおしてみましょう，という回です。

仕事とポテンシャルエネルギー

運動エネルギーと仕事

運動エネルギー$${K}$$を時間で微分してみましょう。

$$
\dot{K}=\dfrac{m}{2}\dot{\left(v^2\right)}=m\dot{\boldsymbol{v}}\cdot\boldsymbol{v}=\boldsymbol{F}\cdot\boldsymbol{v}
$$

$${\boldsymbol{F}}$$が変化していないとみなせるほど小さな時間変化$${\delta t}$$を考えると，

$$
\delta K=\boldsymbol{F}\cdot\boldsymbol{v}\delta t=\boldsymbol{F}\cdot\delta\boldsymbol{s}\ (\boldsymbol{s}\text{は曲線上の座標})
$$

ゆえに，位置Aから位置Bまで，曲線$${C}$$上で線積分すると，

$$
\Delta K=\displaystyle\int_{\text{A},\ C}^\text{B}\boldsymbol{F}\cdot\mathrm{d}\boldsymbol{s}
$$

右辺は比較的すっきりした形をしており，これを，“(外力がした)仕事$${W}$$”と名づけます。

運動エネルギーの，速さの２乗に関する比例定数を$${\dfrac{m}{2}}$$という中途半端な値にしたのは，仕事の形をすっきりさせるためだったんですね……。

ポテンシャルエネルギー

$${W}$$は，基本的には経路によって異なる値をとります。しかし，$${\boldsymbol{F}}$$によっては，始点と終点を決めれば，線積分が経路によらず一定になることがあります。
このような特別な力$${\boldsymbol{F}_\text{cons}}$$(下で述べる理由により”保存力”とよばれる)のする仕事は，移動の経路にかかわらず自動的に加算されてしまうので，移動の経路に依存する項と分けておくと，物理的に意味がありそうです。

保存力$${\boldsymbol{F}_\text{cons}}$$を受けて，曲線$${C}$$上を点Aから点Bまで移動したときの”ポテンシャルエネルギーの変化量$${\Delta U}$$”を，次の式で定義します。

$$
\Delta U=-\displaystyle\int_{\text{A},\ C}^\text{B}\boldsymbol{F}_\text{cons}\cdot\mathrm{d}\boldsymbol s
$$

このとき，保存力以外の力[非保存力]$${\boldsymbol{F}_\text{non-cons}}$$(人が加える力や，摩擦力など)を用いて，

$$
\Delta(K+U)=\displaystyle\int_{\text{A},\ C}^\text{B}\boldsymbol{F}_\text{non-cons}\cdot\mathrm{d}\boldsymbol{s}
$$

この式で，$${K+U}$$のことを力学的エネルギーといいます。すなわち，非保存力がはたらいていないなら，$${\Delta(K+U)=0}$$(力学的エネルギーの保存則)。
力学的エネルギーを保存させるような力なので，$${\boldsymbol{F}_\text{cons}}$$を”保存力”と名づけたのです。

(ちなみに，$${U}$$を”ポテンシャルエネルギー”とよぶのも，このあたりに由来しています。ポテンシャルエネルギーは，将来的に運動エネルギー$${K}$$に変わりうるのです。)

ただ，$${U}$$の定義が$${\Delta U}$$の形になっているのは，不満です。$${U}$$を$${\Delta U}$$の定義から計算すると，

$$
U=-\displaystyle\sum_{k=1}^N\int_{\text{A}_{k-1}, C_k}^{\text{A}_k}\boldsymbol{F}_\text{cons}\cdot\mathrm{d}\boldsymbol{s}=-\int_{\text{A}_0,\ C_1+C_2+…+C_N}^{\text{A}_N}\boldsymbol{F}_\text{cons}\cdot\mathrm{d}\boldsymbol{s}
$$

となるのですが，初期位置を知らないとポテンシャルエネルギーが求まらないのは，ちょっと不便です………。

ここで，次の式を満たす，ポテンシャル$${V(\boldsymbol{r})}$$を考えます。

$$
-\displaystyle\int_{\text{A},\ C}^\text{B}\boldsymbol{F}_\text{cons}\cdot \mathrm{d}\boldsymbol{s}=V(\boldsymbol{r}_\text{B})-V(\boldsymbol{r}_\text{A})
$$

すなわち，

$$
V(\boldsymbol{r})=-\displaystyle\int_{\boldsymbol{r}_0,\ C}^{\boldsymbol{r}}\boldsymbol{F}_\text{cons}\cdot\mathrm{d}\boldsymbol{s}\ (\boldsymbol{r}_0\text{は，適切にとった基準の位置})
$$

こうすることで，初期位置を知らなくても，ポテンシャルエネルギーの変化が分かります(重要なのはポテンシャルエネルギーよりもポテンシャルエネルギーの変化量だけなんですね……)。

めでたしめでたし。

(蛇足ですが，「初期位置のことを”基準の位置”とよび替えただけ」という見方もできます。高校で習う，いわゆる”位置エネルギー”は，この意味で”ポテンシャル”のことです。)

保存力の条件

ところで，保存力は，どのような条件を満たすのでしょうか？

ここで，閉曲線上の線積分[周回積分]を考えてみます。

$$
\displaystyle\oint_{C_1+C_2}\boldsymbol{F}_\text{cons}\cdot\mathrm{d}\boldsymbol{s}=\displaystyle\int_{\text{A},\ C_1}^\text{B}\boldsymbol{F}_\text{cons}\cdot\mathrm{d}\boldsymbol{s}+\displaystyle\int_{\text{B},\ C_2}^\text{A}\boldsymbol{F}_\text{cons}\cdot\mathrm{d}\boldsymbol{s}=\displaystyle\int_{\text{A},\ C_1}^\text{B}\boldsymbol{F}_\text{cons}\cdot\mathrm{d}\boldsymbol{s}-\displaystyle\int_{\text{A},\ C_2}^\text{B}\boldsymbol{F}_\text{cons}\cdot\mathrm{d}\boldsymbol{s}=\displaystyle\int_{\text{A},\ C_1}^\text{B}\boldsymbol{F}_\text{cons}\cdot\mathrm{d}\boldsymbol{s}-\displaystyle\int_{\text{A},\ C_1}^\text{B}\boldsymbol{F}_\text{cons}\cdot\mathrm{d}\boldsymbol{s}=0
$$

さらに，Stokesの定理から，

$$
\displaystyle\iint_S(\boldsymbol{\nabla}\times\boldsymbol{F}_\text{cons})\cdot\boldsymbol{n}\,\mathrm{d}S=0\\\Leftrightarrow(\boldsymbol{\nabla}\times\boldsymbol{F}_\text{cons})\cdot\boldsymbol{n}=0\Leftrightarrow\boldsymbol{\nabla}\times\boldsymbol{F}_\text{cons}=\boldsymbol{0}\ (\boldsymbol{n}=\boldsymbol{e}_x,\ \boldsymbol{e}_y,\ \boldsymbol{e}_z\text{を順に代入すると分かる})
$$

また，保存力とポテンシャル$${V}$$の間には，$${\boldsymbol{F}_\text{cons}(\boldsymbol{r})=-\boldsymbol{\nabla}V(\boldsymbol{r})}$$という関係が成り立ちます。
(実際に代入してみれば分かります。)

まとめておきましょう。

保存力である条件
以下のうち，ひとつを満たせば保存力である。。
①仕事が，始点と終点を決めれば，経路によらず一定
②閉曲線上の仕事が0
③$${\boldsymbol{\nabla}\times\boldsymbol{F}=\boldsymbol{0}}$$
④$${\boldsymbol{F}=-\boldsymbol{\nabla}V}$$を満たすポテンシャル$${V}$$が存在する

運動量と力積

力と運動量の間には，次の式が成り立つのでした。

$$
\mathrm{d}\boldsymbol{p}=\boldsymbol{F}\,\mathrm{d}t
$$

両辺を積分すると，

$$
\Delta\boldsymbol{p}=\displaystyle\int_{t_0}^t\boldsymbol{F}\,\mathrm{d}t
$$

この式の右辺を”力積$${\boldsymbol{I}}$$”とよびます。

演習問題

今回得られた式は二つ。

$$
\Delta K=W:=\displaystyle\int_{\text{A},\ C}^\text{B}\boldsymbol{F}\cdot\mathrm{d}\boldsymbol{s}\\\Delta\boldsymbol{p}=\boldsymbol{I}:=\int_{t_0}^t\boldsymbol{F}\,\mathrm{d}t
$$

これらの式を，”二体問題”とよばれるものに応用してみたいと思います。

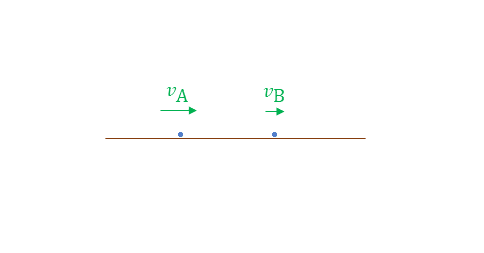
問
図のように，２質点が衝突したとき，それぞれの衝突後の速さはどうなるか。

衝突は嫌だけど………。物理の問題なので………😓

答
力学的エネルギーの保存則は，基準の位置を衝突位置にとることで，

$$
\dfrac{m_\text{A}}{2}{v_\text{A}}^2+\dfrac{m_\text{B}}{2}{v_\text{B}}^2=\dfrac{m_\text{A}}{2}{v_\text{A}'}^2+\dfrac{m_\text{B}}{2}{v_\text{B}'}^2
$$

また，運動量を考えると，作用・反作用の法則から，

$$
\boldsymbol{I}_{\text{A}\to\text{B}}+\boldsymbol{I}_{\text{B}\to\text{A}}=0
$$

ゆえに，

$$
\Delta(\boldsymbol{p}_\text{A}+\boldsymbol{p}_\text{B})=\boldsymbol{0}\ (\boldsymbol{運動量保存則})
$$

であり，

$$
m_\text{A}v_\text{A}-m_\text{B}v_\text{B}=m_\text{A}v_\text{A}'-m_\text{B}v_\text{B}'
$$

これを解いて，$${v_\text{A}'=\dfrac{m_\text{A}-m_\text{B}}{m_\text{A}+m_\text{B}}v_\text{A}-\dfrac{2m_\text{B}}{m_\text{A}+m_\text{B}}v_\text{B},\ v_\text{B}'=-\dfrac{2m_\text{A}}{m_\text{A}+m_\text{B}}v_\text{A}-\dfrac{m_\text{A}-m_\text{B}}{m_\text{A}+m_\text{B}}v_\text{B}}$$を得る。

二つの保存則を確認しておきます。

①力学的エネルギーの保存則
非保存力の合力が0ならば，$${\Delta(K+U)=\Delta(K+V)=0}$$

②運動量保存則
外力の合力が0ならば，$${\Delta\boldsymbol{p}=\boldsymbol{0}}$$

今回はここまでです！
ありがとうございました。

Newton力学編　目次
① 力学とは何か
② 位置の表し方
③ 運動エネルギーと運動量
④ 運動の三法則
⑤ 種々の力
⑥ 仕事と力積　←今ココ！
⑦ 運動方程式を解く
⑧ 回転運動
⑨ 剛体の運動
⑩ 反発係数
◼︎ 章末問題