
アフィン変換が理解出来た気がするので雑に書き殴る
背景
ARKitをよく触っていると、座標変換とかが頻出なので、そろそろ理解しとかないといけないなーと思ってまとめました。
アフィン転換とは?
2次元の画像を拡大したり回転したり変形させることができる座標変換。
アフィン転換の公式

簡潔に言うと「現在地点に行列を掛けて(移動量がある場合は移動量を加えた)場所が、移動後の座標」になります。
行列には移動行列とか回転行列とか色々ありますが、今回は下記の例題で回転行列を使うので、回転行列にしました。
ちなみに上記の式は、以下のように簡潔にまとめることができます。
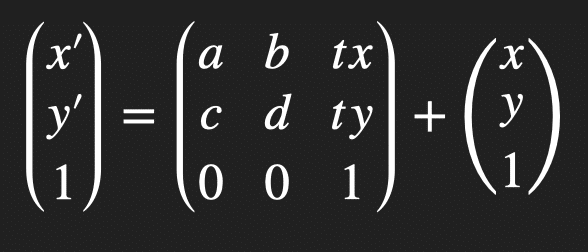
とはいえ、数学のすも分からない人が上の公式を見ながら、いきなりアフィン転換やれ、って言われてもよく分からないと思うので(自分もそうだった)、自分なりに簡単な例題を作ってみました。

例題:4点(x,y)=(1,1)(2,1)(1,2)(2,2)を取るうさぎさんの図形を描画しました。アフィン転換を用いて、これを原点を軸に90°させてください。
移動量=0なので(tx, ty)= (0,0)です。
移動後の座標を求めるには以下の式の答えを出してあげれば良いので

90°の回転行列と現在地の座標を当てはめたものが以下になります。
例)ピンクの座標=(1,1)の場合

となります。
これを掛け算するためには、

の公式を用います。
・ax = 0 * 1
・by = -1 * 1
・cx = 1 * 1
・dy = 0 * 1
よって、ax+by = 0+(-1) = -1, cx+dy = 1+0=1
つまり、ピンク(1,1)の変換後の座標は(-1,1)となります。
同様に水色緑オレンジの座標を変換すると、
それぞれ(-2,1)、(-2,2)、(-1,2)となります。

無事90°変換できましたね。
それでもアフィン転換よく分からないと言う人のために
あまりお勧めしませんがチートシートを自作してみました。
これが正しいかどうかは不明なので、使用は自己責任でお願いします。
・x座標

・y座標

