反力 ~木構造のための構造力学~4
目次
第1回 計算書を読んでみよう(今回)
第2回 力のつりあい
第3回 モーメントとは?
第4回 反力(今回)
第5回 応力
第6回 断面について
第7回 図心・断面一時モーメント
第8回 断面二次モーメント
第9回 断面係数
第10回 許容応力度
力が「なんとなく」わかってきたら、反力を勉強してみましょう。だいぶ構造力学っぽい内容になってきます。しかし仕組みは簡単なので、さらっと理解してみましょう。いきなり数式が出てきて戸惑うと思います。用語の読み方と意味は先に頭に叩き込んでください。苦手意識を持つと後々まで引きずります。特にΣ(シグマ)は意味は単純ですが、理解しておかないと先に進めません。
<反力>
反力とは、物を支える力のことです。手にボールを持ったらボールの重さの反力が手のひらに発生します。もし反力がなかったらボールは下に落ちてしまいます。壁を手で押すと動きませんね?これは手で押す力に対し、壁からの反力があるからです。押し戻されないわけですから手の力と壁の反力は釣り合っていることになります。このように反力は押す力や重さ(外力という)と釣り合っていることになります。
と理屈は簡単です。実際に反力の計算例をみてみましょう。たぶん、実際の式を見ていった方が理解しやすいと思います。ここからようやく力学らしくなります。

上図の反力を求めてみましょう。といっても説明が必要ですね。上図は、左端をピンで支え、右端はローラーで支えている梁です。ピンは鉛直と水平の力を支えます。回転は自由です。ローラーは鉛直だけ支えます。水平の力には抵抗せず、回転もします。上図のような形式を単純梁といいます。非常に多くのケースで利用する基本パターンなので覚えておきましょう。その単純梁の左からLの点に2Pの荷重がかかっているというケースです。LとかPとかは、わかりやすくするために文字で記しています。試験でも多いパターンです。もちろん実戦ではNやmを使います。

反力を求めるには、前提となる力を図に書き込んでいきます。今回の外力は、梁に乗っかっている2Pだけですね?まずは力の向きと荷重を書き込んでみましょう。横からの力などが発生していたらそれも書き込みます。
次に反力を書き込みます。反力は支点にのみ発生します。今回の支点は左右の2箇所です。左側のピンは鉛直と水平を支えます。そのため仮定として鉛直と水平の力を矢印で書き込みます。通常は鉛直の力をV(Vertical reaction)、水平の力をH(Horizontal reaction)と書き込みます。また支点を間違えないように記号をつけます。今回は左をA点、右をB点とします。右側のローラーは鉛直のみ支えるので鉛直の矢印のみを書き込みます。どのような形のモデルであれ、この作業は重要です。必ず書き漏れがないように記入しましょう。
図が完成しましたら、計算に入ります。わからない仮定の力を計算してだしてあげます。今回はVa、HaとVbですね。

まず簡単な部分から解いていきましょう。Haが簡単ですね。なぜなら今回は上からの荷重しかないのです。そこでHa=0ということが計算しないでもわかっています。
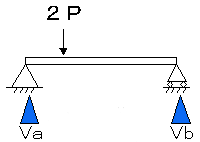
次にVaとVbをだします。上からの2Pの荷重を支える反力は、もちろん上の荷重と同等になります。つまり Va+Vb=2Pとなります。ちなみに2Pが中央にある場合は、VaとVbは同じになるように感じませんか?その通りです。真ん中の場合は計算しなくても左右同じです。問題は今回のように中央にない場合です。
では上記の問題を数学的解法で解いてみましょう。力は動いていない静止状態であれば、つりあっています。つまりすべての反力とすべての外力を合計すれば0になります。これを式で書くとこうなります。
ΣX=0(水平方向の力)
ΣY=0(垂直方向の力)
ΣM=0(モーメント)
です。Σ(シグマと読み)は、難しそうに見えますが「合計」という意味です。ΣXとはX方向の力をすべて足し合わせるということです。ΣYも同様です。ΣMだけは回転する力のモーメントの計なので、それぞれの支点毎に発生するので実際はΣMaとかΣMbのように支点の位置毎に計算します。ただ合計がゼロになる点は一緒です。また単純梁の場合ΣMはどちらか片方の計算で大丈夫なケースが多いです。
では実際に解いていきます。

ΣX=0より、Ha=0
これは、横向きの力が発生していないので、仮定するHa以外の力はありませんね?そこでHa=0が自動的に確定します。
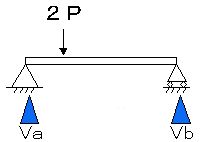
ΣY=0より、Va+Vb=2P
これは、上からの荷重2Pと反力Vaと反力Vbの合計が釣り合っているという意味です。しかしこれでは、VaとVbの合計しかわからず、個別にはわかりませんね?そこで
ΣMa=0
を利用します。もちろんΣMb=0でもかまいません。

ΣMa=0より、2P×L-Vb×4L=0
Vb=0.5P
Va+Vb=2Pより
Va=1.5P
となります。ちなみにΣMb=0でやってみると
ΣMb=0より、-2P×3m+Va×4L=0
Va=1.5P
Va+Vb=2Pより
Vb=0.5P
で同じ事になります。上記計算で難しいのはΣMですね。これだけもう少し解説します。
ΣMa=0ということは、A点でのモーメント(回転)がゼロということになります。モーメントの基本式はM=PLですね?つまり力と距離をかけ算してあげればいいわけです。そして右回りと左回りでは正反対になるので±が逆になります。通常右回り(時計回り)をプラスに、左回りをマイナスとします。
そこで荷重2Pに、A点からの距離Lを掛けたものが、荷重によるモーメントです。A点から見れば時計回りなので、符号はプラスです。次に反力を考えてみます。VaはΣMaに関係がないから考慮しません。なぜならVaをいくら加えてもA点を中心とする回転には関係ないからです。そこで考慮しなければならない残りのVbをつかってモーメントを算出します。反力Vaに、A点からB点までの距離をかけたものが、Vbによるモーメントです。ただしA点を中心としてみると、反時計回りですね?ですから符号もマイナスになります。

次回は、いよいよ応力です。ここまでは応力を理解するための基本知識を学んでいたに過ぎません(それは言い過ぎですが)。応力がわかると構造力学がどのようになっているのかが理解出来ます。ここを建築士試験で暗記で切り抜けると、その後の建築士人生で構造をすっぱりわからなくなってしまいます。覚えるなら、その後に役に立つ方が絶対いいです。別に構造屋にならなくてもこの基本知識は設計で役に立つはずです。
いいなと思ったら応援しよう!