
#05 流れの数値計算 カルマン渦列
隣の専攻の流体工学の講義で出てきて、すぐ興味を持ったカルマン渦。
学術的にもいろいろ面白いんだと思いますが、細かいことはほかにお任せして、自分の手でこれを再現したくていろいろやってみました。
これがリアルで起こるんだからすごい。(動画はDLお願いします)

カルマン渦への道(寄り道)
ネットから論文探したり(参考①、参考②とか)、ソースコードを拾ったりしてfortranでの自作頑張りましたが、、どうしても計算がうまくいかず。。
途中練習で作った二次元キャビティ流れはできました。レイノルズ数の影響も確認できました。
上方壁面に課された境界条件によって渦(1次渦)が発生しており、 レイノルズ数が高くなる(粘性の効果が小さくなる)に従って大きく成長し、発生位置がキャビティ中心に近付くことがわかる。


iRICでの計算
カルマン渦はしばらく諦めていましたが、河川の計算ソフトiRICの存在↓を思い出し、ゼロからは諦めてソフトでの計算に切り替え…!
モデル作成
簡単な水路モデルを作り、障害物セルで角柱を作成しました。
レイノルズ数Re=100~500を狙いたいので、リアルで考えると結構小さい水路です。


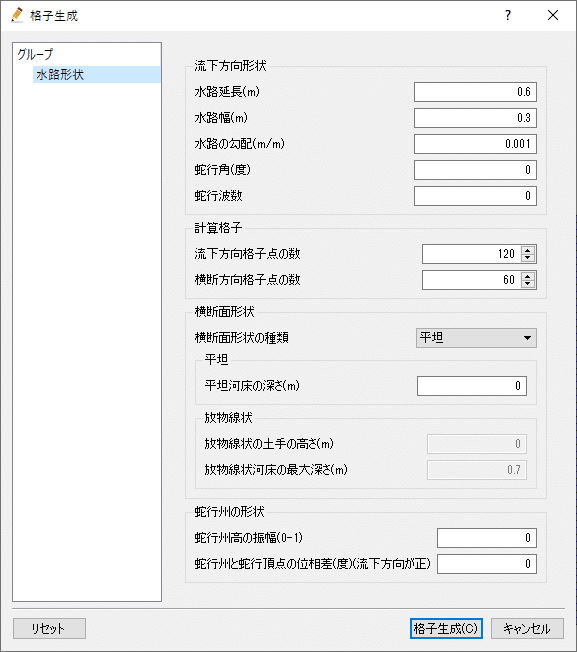
計算条件
条件以下のとおりです。いろいろ試しましたが、レイノルズ数Re=314になりました。格子サイズもΔtも結構小さいです。


計算結果
できた!
振動するところに落ち着くって不思議。


※画像ですみません。動画はDLお願いします。
なぜ計算でカルマン渦が再現できるか
参考にした以下のサイトでこんな記述がありました。
ここまで結果を出力して,ふと思うことがある.
「あれ? なんで振動解(非対称解)が出現しているんだ?」
対称解も解である.また,振動解が解であることもわからないわけではない.
さらに,対称解より振動解の方が安定である,ということもわからないわけではない.自然界では,外乱によってより安定な振動解で遷移しうる,ということもわからないわけではない.
ではなぜこの数値計算で非対称解である振動解への遷移が発生したのか?
考えられることは数値計算上の非対称性,つまり逐次緩和法と数値計算誤差である.
確かに、自然界で発生するカルマン渦は外的な要因をきっかけに振動が発生すると聞いたことがあったが、数値計算上は外的な要因はない。。
しかし、数値計算だと計算誤差が外乱の代わりになって、振動する結果に落ち着くと。自分なりの理解ですが。なるほど。
移流項の扱い
計算条件はすべて同じで、移流項の精度がもう少し落ちる風上差分に切り替えると、振動する渦は発生せず、安定した2つの渦のみとなりました。
繊細な誤差まで捉えるモデルじゃないと渦は再現できない。みたいな理解で個人的には落ち着きました。

※画像ですみません。動画はDLお願いします。
移流項については以下が詳しいです。
おわり
何とかできました。
引き続き水理学をベースに、現象の再現と理解を深めてみます。次は、3次元の計算で二次流を見てみたいと思っています。
noteでも探してみると、理論からきちんと考えておられる記事がありました。非常に参考になります。
お時間あれば、以下ものぞいていってください。
この記事が気に入ったらサポートをしてみませんか?
