#04 流れの数値計算　差分法

shino

2023年4月30日 12:18

前に書いた基礎式に続き、差分法について。備忘録です。
前にいろいろつくったものの、自己満で終わっていたのでここに記しておきます。

ここでプログラムを少し書いて、動くようになってやっと面白くなってきた感じです。

差分法とは

微分方程式をコンピュータで解くために、デジタルな情報に離散化する手法の一つです。有限要素法もよく聞く手法の一つだと思いますが、正直あまりピンときませんでした。差分法とても分かりやすい。

当時はプログラムが付いた以下の本をすごく読みました。

本買ったときは全然知らなかったですが、この著者の講義を受けていたことを後から知って、それ以降その先生がめちゃくちゃかっこよく見えたのをよく覚えています。

最近は、iRICのホームページから令和版「現場の水理学」の中でもわかりやすい差分法の記載があるので非常におすすめです。すべてフリーなんだからすごい。

つくったもの

細かい解説は上記に譲って、自分の作ったものを載せていきます。
簡単な一次元で、ナビエストークス式にも関係する移流方程式と拡散方程式の数値解の挙動を見てみます。

一次元移流方程式

式は以下です。解析解を見ればわかりますが、一様に同じ形で移動する挙動を示します。

$$
\cfrac{\partial f}{\partial t}+c\cfrac{\partial f}{\partial x}=0
$$

ただ、これを色んな差分の取り方で解いてみると挙動が違って、「計算が不安定になるんだよなあ」みたいな玄人の会話の意味が少しわかった気になります。

どの場合にも解析解として、(+)側に移動するだけの放物線を入れています。
教科書で見るような結果なのに、自分でできるととてもうれしい。手を動かすって重要。

①前進差分：安定するが、解が減衰する（なまる）。
②後退差分：不安定。発散。
③中心差分：高精度だが、少し不安定。

同じ前進差分でも次数を上げると精度も上がってきます。
若干減衰しますが、一次よりいい感じ。

…位相のずれについてはよくわからずです。未熟です。

一次元拡散方程式

式は以下です。文字通り拡散する様子が見れます。
移流方程式の前進差分には、意図せずこの項が出てくるため、解が減衰するような挙動が生じます（数値拡散）。

$$
\displaystyle{{{\partial f}\over{\partial t}}=D{{\partial^2 f}\over{\partial x^2}}}
$$

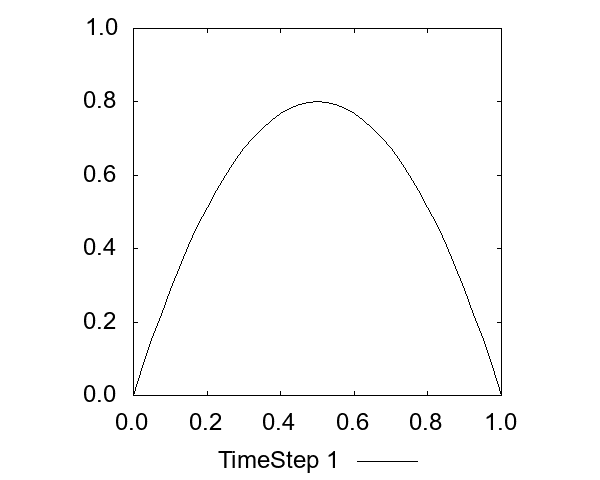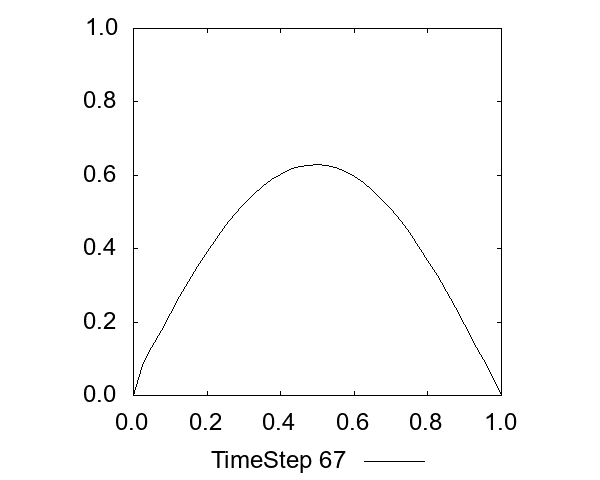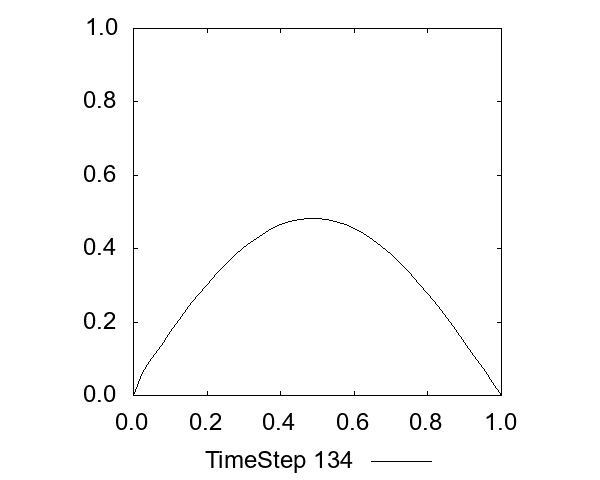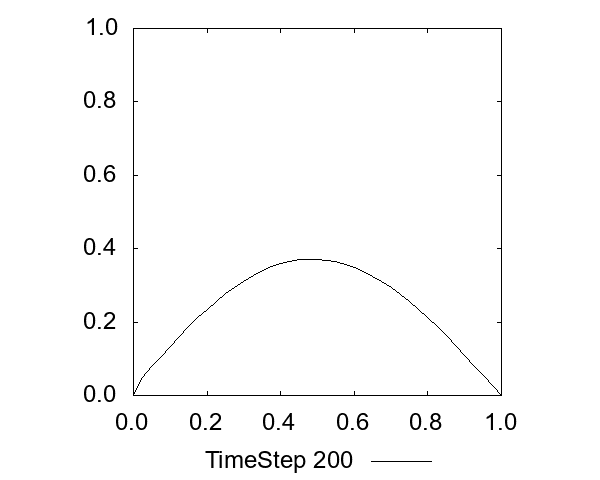
CFL条件

上記の計算をする際、時間については前進差分を取っていますが、陽解法となるため、Δtの取り方に留意する必要があります。

基本は、CFL条件を満たすように取ります。小さければ安定しますが、計算負荷がどんどん大きくなります。

その運動方程式の数値解を求める際に用いる時間ステップΔt の値は、実際の波動が隣り合う格子に伝達するまでの時間よりも小さくなければならない。もしΔt の値がその時間の上限を超えると、計算上の情報伝達速度が実現象の速さに追従できずに数値発散が生じてしまい、物理的に意味の無い解を得てしまう。意味のある計算をするためには空間格子の間隔Δx を小さくするなら、時間ステップΔt の上限値もそれに伴って減らさなければならない。

CFL条件 - Wikipedia

一次移流方程式の場合、

$$
v \frac{\Delta t}{\Delta x} < 1
$$

一次拡散方程式の場合、

$$
\Delta t\leq\frac{\Delta x^2}{2 D}
$$

もちろんiRICの方でも解説出ています。

ソースコード

Fortranで書いて、Gnuplotでアニメにしていました。当時は無料でここまでできてすごいよろこんだ覚えがあります。
Gnuplot気に入っていたけど、使う機会減ってしまった。。

計算本体の方は、最初に紹介したサイトにpythonのコードがオープンになっているので、Gnuplotだけでも紹介。
pythonならグラフまできれいにできるもんなあ。

#Setting terminal
set terminal gif animate delay 10 optimize size 600,480 font "Arial,18"
#Setting file
filename = "Diffusion"
set output filename.".gif"

#Setting gragh
set size ratio -1
set xrange [0:1]
set yrange [0:1]
set xtics 0,0.2,1.0
set ytics 0,0.2,1.0
set format x "%2.1f"
set format y "%2.1f"
set title font "Arial,18"
set key center below

do for [i=1:300] {
  data = sprintf("t_step%03d.dat", i)
  plot data using 1:2 with line title sprintf("TimeStep %d", i) lc "grey0",\
}

…サムネイルは無限階段使わせていただきました。数値計算って、境界から順々に計算していって階段みたいって。