
回転位置エンコーディングによるGPTの改善
記事について
LLamaの論文『LLaMA:OpenandEfficient Foundation Language Models』のセクション2.2では、基本となるアーキテクチャ『Attention Is All You Need』からの変更点について述べられています。その変更点の一つとして、Rotary Positional Embeddings(回転位置エンコーディング)の使用が挙げられています。この手法を最初に提案した論文『RoFomer: Enhanced Transformer With Rotary Position Embedding』が参照されています。
アテンションメカニズムには位置を認識する仕組みがないため、トークンの位置情報を別途準備する必要があります。『Attention Is All You Need』の論文では、絶対的な位置情報を事前に数値として設定しています。他の手法として、位置埋め込み層を導入し、位置情報をモデルが学習するようにする方法もありますが、論文によるとどっちの手法を使ってもほぼ同じ結果が得られたとのことです。
この記事で取り上げる回転位置エンコーディングでは、二つのトークンの相対的な距離をそれぞれのベクトル表現からなる角度の差から計算しています。また、回転位置エンコーディングをアテンションを計算する直前のクエリとキーのみに適用しているところが前との大きな違いです。
回転位置エンコーディングの導入が改善に寄与するかどうか、素朴な疑問から検証を行うことにしました。
検証の設定とソースコード
トランスフォーマーのデコーダーモデルは過去の記事で取り上げたアーキテクチャを使用しています。
元々のアーキテクチャでは、位置エンコーディングが最初に配置されていますが、Llamaで導入された回転位置エンコーディングは、クエリ(Q)とキー(K)が積を取る前に適用されます。

ソースコードは以下に配置しています:
デコーダーモデルはAndrej Karpathy氏のソースコードを基にしており、回転位置エンコーディングはLlamaのソースコードから参照しています。この回転位置エンコーディングをKarpathy氏のコードに組み込み、使用するエンコーディングを引数で選択できるようにしました。これにより検証が容易になります。
今回検証に使用したパラメータ数やデータセットは
・数百万程度のパラメータ数の小規模モデル
・シェイクスピアのデータセット
・トークンはキャラクターレベル
回転位置エンコーディング
回転位置エンコーディングについて簡単にまとめます。
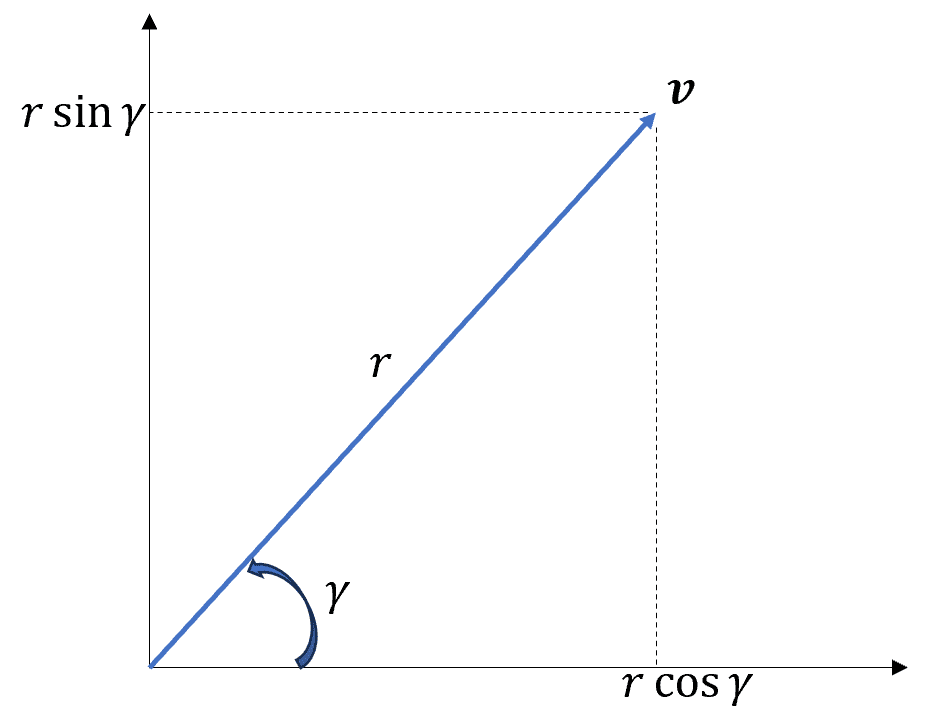
二次元ベクトル$${\textbf{v} = (x, y)}$$を複素数で表現することができます。
$${\textbf{v} = x + i y = r \cos\gamma + i r \sin\gamma = r e^{i \gamma}}$$
最後の等式はオイラーの公式です。
また、ベクトル$${\textbf{v}}$$に$${e^{i \theta}}$$を乗じると、$${\theta}$$だけの回転が作用します。
$${\textbf{v}e^{i\theta} = r e^{i(\gamma + \theta)}}$$
これを展開してみると、
$${\textbf{v}e^{i\theta} = (x + i y) (\cos\theta + i \sin\theta ) = x \cos \theta - y \sin\theta + i (x \sin\theta + y \cos\theta)}$$
実部と虚部をベクトルの成分として見ると、次の行列操作と等価です。
$$
\begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{pmatrix}
\begin{pmatrix}
x \\ y
\end{pmatrix} =
\begin{pmatrix}
x\cos\theta - y\sin\theta
\\ x\sin\theta + y\cos\theta
\end{pmatrix}
$$
上記の行列はユニタリ行列で、ベクトルを引き伸ばしたりはせずに回転のみの変換をします。
$${m}$$番目に位置するトークンに作用する行列を
$$
R_m = \begin{pmatrix}
\cos m & -\sin m \\
\sin m & \cos m
\end{pmatrix}
$$
として、$${m}$$番目のクエリ、$${n}$$番目のキーへの回転位置エンコーディングは以下の変換になります。
$${\textbf{q}_m \longrightarrow R_m \textbf{q}_m, \quad \textbf{k}_n \longrightarrow R_n \textbf{k}_n}$$
アテンションの計算時には、上記のクエリとキーの内積を取ります。ここで、角度の差$${(𝑚−𝑛)}$$が相対的な距離に影響します。
これまでは2次元のケースでの説明でしたが、多次元の場合も同じようにユニタリ行列で回転を行います。
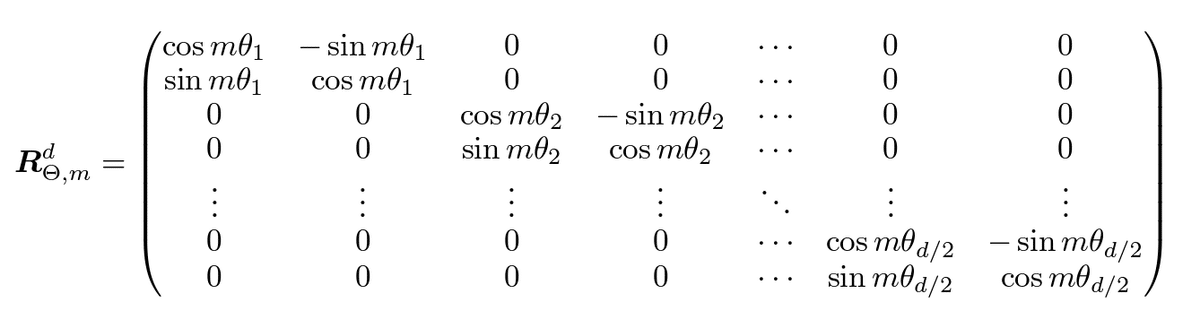
$${\theta_i = 10000^{-2(i-1)/d}, \quad i = 1, 2, \ldots, d/2}$$
このユニタリ行列は、二つの要素ごとに回転を行っているというイメージです。例えば、4次元($${𝑥_1,𝑥_2,𝑥_3,𝑥_4}$$)の場合、$${𝑥_1}$$-$${x_2}$$ 平面に垂直な軸を基に回転し、また $${𝑥_3}$$-$${𝑥_4}$$ 平面に垂直な軸を基に回転します。このユニタリ行列が他のものに比べて有効かどうかは不明ですが、わかりやすいのが特徴です。
$${\theta_i}$$ に関して、この値がとる範囲は $${1}$$ から $${0}$$ に近い値($${10000^{-(d-2)/d}}$$)までで、非常に急速に 0 に近づきます。
$${\theta_i}$$のみだと微小な回転ですが、トークンの位置の差分($${m-n}$$)が大きいと、ある程度の回転が起きることになります。そしてクエリとキーの内積の結果がその分小さくなります。
結果
青線:回転位置エンコーディング
オレンジ線:位置埋め込み
緑線:位置情報なし
学習データと検証データから損失の評価をそれぞれ以下に記載しています。

回転位置エンコーディングの場合、前半の減少が速く一番低く減少を続けています。ここまで効果があるんだと少し驚いています。

回転位置エンコーディングの場合、損失の減少が一番早く、5000ステップ辺りから過学習の傾向がみられます。
回転位置エンコーディングの効果を垣間見た程度ですが、良さそうな感じです。
ちなみに、文章の生成を行ってみると以下のような形で生成されます。改行(\n)から始めて生成を行っています。割と英語っぽい文章が生成されているかと思います。(学習データがシェイクスピアなので理解が難しいです。。)
ROMEO: Stake the directitude to be rain!
PETRUCHIO: The benefit of my dear proph, ere were God! O place, thy turn swift against those Thanking thy sinews thusets, privil'd-royar, Though for thy lenealce from mine enemy: Thou, many corse; the truth to endure gound.
CLARENCE: Sirrah, but to thy father's charge the palate! Soft! for whoso followers shall not stand: I will thy contrary forth of these dears? Reads, lay.
BUCKINGHAM: My lord, here consul is Surrey, So Thursday Plantagenet. Lady: these will after: Commend and noble king, the happy curse I seen us in his reposed of a pushond fast. Who dares for us? 'tis it become the cause. Messenger: Had slaid an oath nor guess To make me, whisper so her army Beauty senator: sits my needs wold, I she And put it on me, that ever it, so cripely Stand up good town so glir with your king. Now, afre you log; not as if you stain,-- Were not are the went with the cobject, For haltive stone posk without hearing sweet, And that way thrive mine, who
読んでいただきありがとうございました。何かのお役に立てばうれしいです。また気になる点や質問等などありましたらお気軽にお問い合わせください。
