大平洋クロマグロ急増の原因 ー それは、MSY理論に基づく資源管理を行うと、実際には不必要である過大な漁獲量の削減が必要となり、その過大な漁獲量削減が結果的に資源を急増させるからである ー
注) MSY理論とは、持続的に漁獲することができる最大の漁獲量(この漁獲量をMSYという)が達成できる資源水準が存在するという理論。この理論は、資源変動は密度効果(本文参照)によって生じるという考え方をもとに導き出されたのもである。従って、MSY理論は密度効果の存在が、不可欠の前提となっている点に注意する必要がある。
1.はじめに
太平洋クロマグロは、2015年から漁獲可能量(TAC)による漁獲規制が実施された。漁獲規制は21年後の2035年に親魚量を20%B0(B0は漁獲がないと仮定したときの親魚量)に回復させるという目標のもとで実施された。しかし、予定よりも13年も早く、たった8年で親魚量は20%B0以上まで回復したことが明らかとなった [1]。
親魚量が早期に回復したので、管理は大成功であると評価する人もいるが、「厳しい漁獲量削減によって壊滅的な打撃を被った沿岸零細漁業者の方々の惨状をみると、果たしてこのような厳しい漁獲量削減を強行する必要があったのか!」、私は、その妥当性については厳しく問われるべきであると考えている。
なぜ、21年もかかるはずの管理目標が、たったの8年で達成されてしまったのか? それは「海洋環境などがたまたま良かったから」等の偶発的な事情が原因ではなく、「なるべくしてなった当然の帰結である!」と言えるところに大きな問題がある。なぜなら、MSY理論に基づいて資源管理を実施すると、実際には不必要である過大な漁獲量の削減が必要となるため、その過大な漁獲量の削減が、結果として資源を急増させることになるからである。そのことを説明するのが、本記事の目的である。
2. WCPFC が採用している再生産モデル
WCPFC(中西部太平洋まぐろ類委員会)はMSY理論に基づき資源管理を行っているが、それを実施するためには、密度効果が内在する再生産モデルを仮定する必要がある。再生産モデルとは、親魚量と加入量(0歳魚尾数)の量的な関係を表す図または数式のことを言う。また、密度効果とは親魚量が増大することによって、餌や生息場所の競合等により、死亡率が高まったり、成長率が悪くなったりして、結果として加入量の増大が抑制される現象を言う。WCPFCは再生産モデルとして図1の赤い線で示したようなホッケー・スティックモデルを用いている。ホッケー・スティックモデルと呼ばれる理由は、この再生産モデルがアイスホッケーで使うスティックのような形をしてるからである。
太平洋クロマグロに適用されているホッケー・スティックモデルは、親魚量が0から1万㌧ぐらいまでは、親魚量の増大に伴って急激に加入量も増大するが、親魚量がそれ以上になってしまうと、強い密度効果が働き、加入量が一定になってしまうという形状をしている。

図中の点は、実際の再生産関係のデータである。緑色の点線で示した実際に親魚量のデータが存在する範囲に対しては、x‐軸に平行のフラットな直線が当てはめられているが、実際のデータはその上下に大きくばらついており、ホッケー・スティックモデルとデータは大きく乖離していることがわかる。さらに、紫色の点線で示した親魚量が0-1万㌧ぐらいの間のほとんど垂直に近い比例部分に対応する範囲には、再生産関係のデータが全く実在していない。「データが全くないところに、こんな線を強制的にひいてしまってはいけない」というのが統計学の常識であるから、このように大きくばらついている無相関のデータに、ホッケー・スティックモデルを当てはめること自体に、科学的正当性は全くないということになる。
このような非科学的なホッケー・スティックモデルを使って、シミュレーションを行い、将来予測を行うと、必ず、漁獲量削減効果を過小評価することになってしまう。なぜなら、例えば、親魚量が2-3 万㌧レベルの時に、厳しい漁獲規制を実施することによって、親魚量を10万㌧に増やしたとしても、あるいは、15万㌧に増やしたとしても、加入量は、親魚量が2-3万㌧の時と全く同じで変化がないので、「親魚量を増加させたことにより得られるメリットが全くない」ということになるからである。すなわち、「上記のように、ほとんどx-軸に平行なホッケー・スティックモデルを想定している限り、いくら漁獲量を削減し、親魚量を増やしたとしても、全く加入量の増加にも、その結果として期待される親魚量の増加にも寄与しない」という結果になることは、図1を見れば明白であろう。
逆に言い方をすると、過大な漁獲量の削減を実施すればするほど、漁獲規制の効果は相対的によりひどく過小評価されることになる。これが、「クロマグロの小型魚の漁獲量を50%も削減するという、とんでもなく厳しい漁獲規制」を強行したにも関わらず、その効果を過少評価し、目標達成には21年もかかるという誤った予測を行うことになってしまった原因であり、また、実際には予定の半分以下のたった8年で目標が達成されてしまった原因である。
一言で言うと、「x-軸に平行なホッケー・スティックモデル用いている限り、親魚量増大の効果が全く反映されないので、漁獲量削減の効果が過小に評価されてしまう」ということである。
3. 水産庁は「再生産関係に明確な相関関係が認められない」と述べているが、それは、環境変動を無視しているからである
図2は水産庁が提示する太平洋クロマグロの再生産関係の解説を示したものである[3]。 オレンジ色と水色の丸が実際の再生産関係のデータである。図中の水色の丸は、同じぐらいの親魚量にも関わらず、2016年は加入量が高く、2017年と2018年は加入量が低かったことを示している。また、水色の大きな丸で囲ったところは、「親の数が少ないのに、子の数が多い」年を、また、緑の大きな丸で囲ったところは、「親の数が多いのに、子の数が少ない」年を示している。以上のことから、水産庁は「親魚量と加入量の間には、明確な相関関係は認められない」と結論づけている。
再生産関係のデータが、なぜ、こんなにばらついてしまうのか? 本当に、「加入量は親魚量とは無関係に決まってしまうのか?」ということであるが、もちろんそんなことは生物学的にありえない。このような図になってしまうのは、環境変動を無視しているために「見かけ上、相関がないように見えてしまうだけ」ということである。

筆者は、環境変動を取り入れることによって、太平洋クロマグロの再生産関係の再現が可能であることを示している「5, 6」。また、一般に、再生産関係のパターンは、増加傾向を示すパターン、減少傾向を示すパターン、全く無相関となるパターン、の3つのパターンに分類することが可能で、さらに、再生産関係を表すそれぞれの点は、年次が進むにつれて、時計回り、もしくは反時計回りの2つのパターンに分類することができるので、結局、再生産関係は6つのパターンに分類することができることを示している。また、なぜ、そのような6つのパターンが出現するのか、そのようなパターンが表れるメカニズムについても、環境変動の周期と成熟するまでの年数との関係によって、どのパターンになるかが決定されることを示している(7-8)。詳細は、文献(5-8)をご覧いただくことにして、この記事では、「MSY理論では漁獲量の削減効果が必ず過小評価されてしまう」というメカニズムについて、さらに視覚的な説明を進めることにする。
4. 環境変動を取り入れた新しい再生産モデル ー これを「放射線状モデル」と呼ぶことにしよう! ー
図3は図2で示した再生産関係に環境変動を取り込んだ場合の新しい再生産関係のイメージを模式的に示したものである。再生産関係のデータは図2と全く同じであるが、図3にはホッケー・スティック モデルの代わりに、原点を通る複数の直線が描かれている。それぞれの直線が環境変動によって決まる再生産関係を示し、それぞれの直線の傾きが環境の良し悪しを表している。例えば、赤で示した直線は、太平洋クロマグロにとって極めて海洋環境が良かった時の再生産関係を示している。反対に、紫色で示した直線は、太平洋クロマグロにとって極めて海洋環境が悪かった時の再生産関係を示している。

従って、この新しい再生産モデルでは、親魚量が低レベルで2万㌧ぐらいの時でも、赤い線で示したようにその時の環境条件がいいと、加入量は高いレベルになり、親魚量が10~15万㌧ぐらいの高いレベルにあっても、紫の線で示したようにその時の環境条件が悪いと、加入量は赤で示した直線の場合よりも低いレベルになってしまうこともある、ということを示している。
実際には、直線の数は点の数だけ引くことができる。点の数だけ直線を引くということは、再生産成功率を用いることと同じことになる。ここで、再生産成功率とは、「加入量 ÷ 親魚量」のことであるから、各々のデータと原点を結んだ直線の傾きは、再生産成功率そのものということになる。図3に示した形状のイメージから、図3に示した再生産モデルを「放射線状モデル」と呼ぶことにしよう。ここで大切なことは、放射線状モデルでは、密度効果は一切仮定されておらず、その点がホッケー・スティック モデルと大きく異なるということである。
さらにここで重要なことは、放射線状モデルは、海洋環境が同じであれば、親魚量が多いほど、加入量も多くなり、その傾向はどの直線でも同じであるので、放射線状モデルは「海洋環境の良し悪しに関わらず、親魚量が多いほど、加入量も多くなるという特性をもっている」ということになる。
この点が、ほとんどの親魚量レベルで、親魚量の大小とは無関係に、加入量が一定になってしまうホッケー・スティック モデルと決定的に異なる点である。従って、放射線状モデル(再生産成功率)を用いると、どのような環境状態であろうと、漁獲量を削減して親魚量を増大させることの意義が(もちろん、環境状態によってその効果の大きさは異なるが)、漁獲規制の効果としてちゃんと反映されることになるので、ホッケー・スティック モデルを仮定した場合とは、結果が大きく異なるということになる。
以上が、「環境変動を無視し、x-軸に平行なホッケー・スティック モデルに基づいて漁獲量の削減効果を判定するシミュレーションを行うと、必ず、漁獲規制の効果が過小に評価されてしまう」というメカニズムの説明である。
5. 「ゴマサバ東シナ海系群に対してMSY理論に基づく資源管理を実施した場合のシミュレーション結果
水産研究・教育機構は、「もし、過去に新しい水産資源の管理を実施していたら?」どうなっていたかということを、ゴマサバ東シナ海系群に対して行ったシミュレーションの結果を、2019年に発表している(水産経済新聞の2019年8月5日版、図4)。水産庁が推進する「MSY理論をベースとする」新しい水産資源の管理を2003年から実施した場合を想定し、「新管理を実施することで、親は3倍、漁獲量も1.5倍」になると述べ、MSY理論をベースとする新しい水産資源の管理の有効性を強調している。

しかし、この図を一見すると、「なんか変!」ということにすぐに気がつく。なぜなら、後ほど詳しく説明するように、新しい水産資源の管理を実施しているのであれば、再生産関係としてホッケー・スティック モデルを用いているはずであるが、図4 の真ん中の図に示されているように、2005年あたりから親魚量は8.5万㌧以上になっているのに、図4の左の図に示されているように、2005年以降の加入量は一定にはならず、大きく変動しているからである。すなわち、ホッケー・スティック モデルが使われていないことは、図を見ればすぐにわかる。
6. 再生産関係としてホッケー・スティック モデルを用いた場合のシミュレーション結果
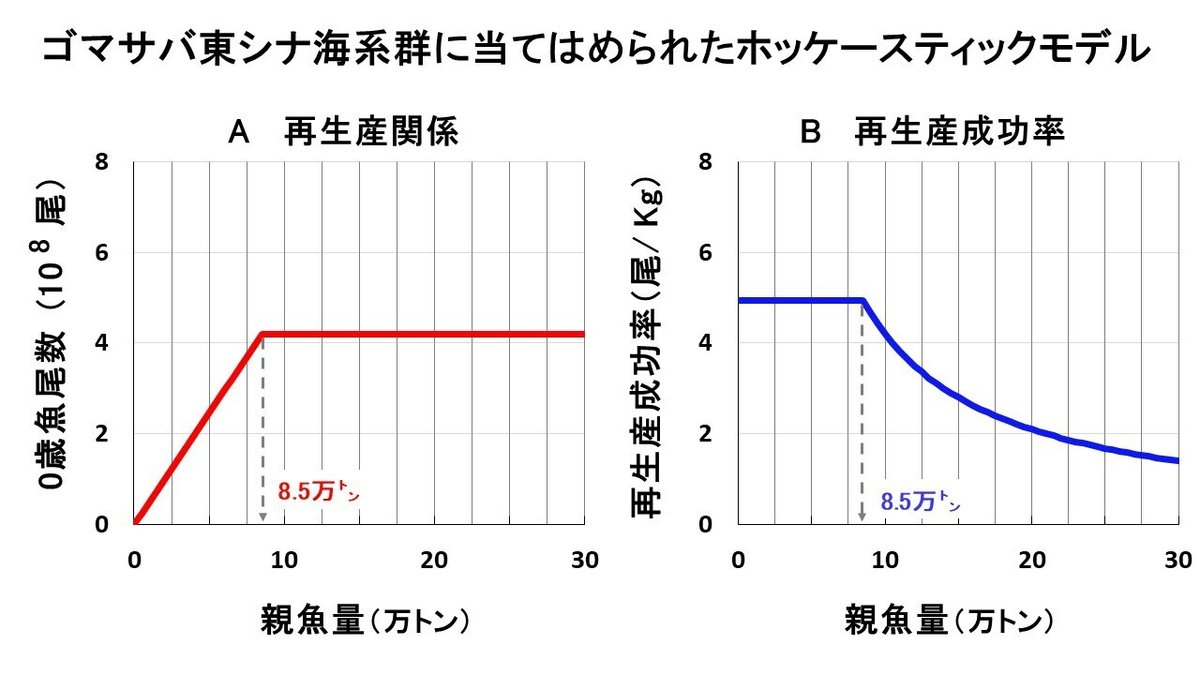
既に述べたように、MSY理論に基づいて資源管理を実施する場合は、密度効果が内在する再生産モデルを仮定する必要がある。今回、新しい水産資源の管理の適用対象となったゴマサバ東シナ海系群の再生産関係としては、図5Aにおいて赤い線で示したようなホッケー・スティック モデルが使用されている。まず、原点と親魚量の最大値8.5万㌧とそのときの加入量4.2億尾の点(図中、赤丸で示した)を直線で結び、親魚量がそれより大きくなると、加入量は4.2億尾で一定となることを仮定している。
しかし、「ここで注意しなければならないのは、8.5万㌧は親魚量データの最大値であるから、「親魚量がそれ以上のデータは存在しない」ということである。データがないのに、どうして親魚量が8.5万㌧以上になると、加入量が一定値となると言えるのか、その根拠は全く示されていない。ただ単に、一定値になると勝手に仮定しているに過ぎない。

親魚量が8.5万㌧以上になった場合のデータがないので、1つの可能性として、親魚量が8.5万㌧以上になると、加入量は一定値になるということを仮定する(これを「ケース1」と呼ぶことにする)こと自体はいいとしても、それに対するもう一つの可能性として、「そのまま直線的傾向が続いていくケース(これを「ケース2」と呼ぶことにする)」も当然考えないと、「片手落ち」ということになる。水産研究・教育機構が行ったシミュレーションは、この「ケース1」の場合しか検討していないということが、まず、第1の大きな問題であると言える。
両者を比較するために、まず、ケース1の場合、すなわち、図5Aにおいて、赤で示したホッケー・スティック モデルを用いた場合について、シミュレーションを実施した。シミュレーションでは、MSYを与える漁獲係数 (FMSY)を使用した場合を想定した。 FMSY の値は、0歳魚は0.36、1歳魚は0.47、2歳魚以上は0.66と推定されている [4]。シミュレーションの結果を図5のBからDに示した。
図5Bは、加入量を示す。黒い線が実際のデータ、赤い線がシミュレーション結果である。図5Cに示すように、2008 年から親魚量が8.5万㌧を超えるので、ホッケー・スティック モデルに従って、加入量は一定値4.2億尾になっている。図5Cは、既に述べたように親魚量を示す。黒い線が実際のデータ、赤い線がシミュレーション結果である。x-軸に平行な青い点線は、加入量が一定値になる時の親魚量8.5万㌧を示す。同様に、x-軸に平行な緑の点線は、MSYを与える親魚量水準(BMSY)を示す。2008年から親魚量が8.5万㌧を超え、その後そのまま増加して、BMSYの周りで小さく変動しながら、BMSYを維持していることがわかる。図5Dは、漁獲量を示す。x-軸に平行な緑の点線は、MSY(7.6万㌧)を示す。
従って、MSY理論通り、FMSYで操業した場合には、親魚量はBMSYを維持し、また、漁獲量はMSYを維持する結果となっていることがわかる。「めでたし!、めでたし!」ということになるのだが、どういうわけか、図5は図4と全く異なった形状を示していることがわかる。しかも、漁獲量は確かに現行(黒い線)1.5倍程度になっているが、親魚量は現行の3倍ではなく、2倍程度である。いったいこれは、どういうことであろうか? どうして図4と図5は一致しないのだろうか?
7.再生産成功率を用いた場合のシミュレーション結果
次に話を進める前に、漁獲係数について整理しておくことにする。表1は、管理を実施すると仮定した2003年から2017年までの漁獲係数の平均値(これをmと記すことにする)、FMSYの値、FMSYの値がその平均漁獲係数mを何パーセント削減した値に相当するか(削減率として表記)、また、その削減率を半分にしたと仮定した場合の漁獲係数(「削減率半分」と表記)を、それぞれ示した。

図6の黒い線は、ゴマサバ東シナ海系群に対して実際に使われたと推定される漁獲係数の推移を示す。また、表1に示したFMSYの値を赤い線で、2003年から2017年までの漁獲係数の平均値を緑の線で、「削減率半分」の漁獲係数の値を青い線で、それぞれ示した。FMSYの値は、実際に使われた漁獲係数を20%から35%削減したものであるが、図を見ると、実際に使われた漁獲係数の一番小さい値に近く、実際には、「相当厳しい漁獲規制を実施することになる」ことがわかる。

図7は、「削減率半分」の漁獲係数(表1の青字で示した値、図6の青色で示した線)を用い、再生産モデルとして図5に示したケース2のモデル(再生産成功率を用いるということ)を仮定した場合のシミュレーション結果を示した。
図7Aは、再生産成功率を、図7Bは、加入量を、図7Cは、親魚量を、図7Dは漁獲量をそれぞれ示す。いずれの図も、黒い線が実際のデータ、赤い線がシミュレーション結果を示す。

表2は、図5と図7に示したシミュレーションの条件を整理して示したものである。図5は再生産関係としてホッケー・スティック モデルを用い、漁獲係数としてFMSYを用いたシミュレーション結果である。図7は再生産関係として再生産成功率(放射線モデル)を用い、漁獲係数として削減率半分を用いた場合のシミュレーション結果である。図8については、後ほど述べる。

図5と図7を比較すると、図7は漁獲係数の削減率が図5の場合の半分であるにも関わらず、図5の漁獲量が現行の1.5倍であるのに対して、図7の漁獲量は現行の2.8倍程度とはるかに大きい。親魚量についても図5が現行の2倍程度であるのに対して、図7は現行の3倍程度とはるかに大きい。。すなわち、ホッケー・スティック モデルを用いた場合は、極めて大きな漁獲係数の削減を行っているにも関わらず、親魚量の増大は2倍程度、漁獲量の増大は1.5倍程度の伸びにとどまっているのに対して、再生産成功率を用いた場合は、漁獲係数の削減率は、上記の半分と小さいにも関わらず、親魚量も漁獲量も3倍程度まで増大していることがわかる。
このことは、既に述べたように、ホッケー・スティック モデルを仮定して将来予測を行うと、極めて大きな漁獲量の削減を実施しても、親魚量も漁獲量もそれほど増大せず、漁獲量の削減の効果は過小にしか評価されないということを示している。
もし、ホッケー・スティック モデルが実際の資源の再生産関係をうまく表しているモデルであるならば、親魚量をMSY水準に回復・維持し、漁獲量をMSYに増大・維持するためには、そのような極めて大きな漁獲量の削減も避けられないということになるわけであるが、残念ながら、実際にはそうではないということを、太平洋クロマグロ資源が証明してくれたわけである。すなわち、太平洋クロマグロ資源が予定よりも13年も早く、たった8年で管理目標に到達したことは、環境条件等がたまたまよくて偶発的にそうなったというわけではなく、ホッケー・スティック モデルを仮定したことによって、不必要に過大な漁獲量の削減が必要とされ、その過大な漁獲量削減を実行した結果として、必然的に極めて短期間に親魚量が管理目標に到達したということである。
8. 2019年8月5日に水産経済新聞に掲載された図は、捏造?
ところで、最後に残った問題は、「なぜ、図4に示した水産経済新聞に掲載されたシミュレーション結果と図5が一致しないのか」ということである。そこで、図4に示されたシミュレーション結果と一致するように、いろいろ制約条件等を設定して検討してしてみることにした。試行錯誤の結果、以下のようにすると、図4の再現が可能であることがわかった。

図8をみると、多少、数字の相違はあるかもしれないが、変動パターンは、図4に示した水産経済新聞に掲載されたシミュレーション結果と非常によく一致していることがわかる。どのような設定をすれば図8のような結果が得られるのかということを次に述べる。
まず、再生産関係としては、本来用いるべきホッケー・スティック モデルは用いずに、なぜか、再産成功率を用いている。漁獲係数は、FMSYという極めて小さな値を用いているので、図7の結果から予想できるように、親魚量や漁獲量はかなり大きな値になるはずである。実際計算するとそうなることは、確認済みである。親魚量や漁獲量がかなり大きな値になってしまうと、FMSYのような小さな漁獲係数を使う必要はない(漁獲量を大きく削減する必要はない)ということになってしまうので、FMSYを使うことを正当化しようとすれば、親魚量や漁獲量があまり大きくなってしまわないような、制約条件が必要になる。そこで、加えられた制約条件が以下になる。
「計算される親魚量が8.5万㌧を超えた場合は、その親魚量の値を8.5万㌧
に置き換え、「再生産成功率 × 8.5万㌧」で、加入量を計算する。」
このような条件が使われていることは、2006年以降の図8Aの再生産成功率の変動パターンと、図8Bの加入量のパターンがほとんど同じであることからもわかる。
ホッケー・スティック モデルは親魚量が8.5万㌧以上になると、密度効果の影響で加入量が一定になってしまうという再生産モデルであるが、上に示した制約条件は、ホッケー・スティック モデルを用いる代わり、親魚量が8.5万㌧以上になると、加入量は観測された再生産成功率に8.5万㌧を掛けて計算するという意味不明の計算式を用いてシミュレーションを実施している。しかし、この加入量の計算方法とホッケー・スティック モデルとの関係は不明である。このような計算を行うことの科学的正当性を、まず説明すべきではないだろうか?
上記のことを検討するために、図9に、ホッケー・スティック モデルと再生産成功率の関係を示した。親魚量が8.5万㌧以上になると加入量が一定になるということは、親魚量が8.5万㌧以上になると、密度効果の影響で再生産成功率は急激に減少していくことを意味している。
関係
図10は、図8に示した数値を用いて、図9Aに相当する再生産関係と図9Bに相当する親魚量と再生産成功率の関係を図示したものである。親魚量が8.5万㌧以上になると、加入量は再生産成功率 × 8.5万㌧で計算されるので、加入量の変動は、再生産成功率の変動そのものを示していることになる。
同様に、再生産成功率は親魚量が8.5万㌧以上になると、加入量は再生産成功率 × 8.5万㌧で計算されるので、図10Bの再生産成功率は、親魚量とは無関係に再生産成功率そのものの変動を示していることになる。従って、図9Bに示したような減少傾向を示すことはない(統計的検定によりチェック済み)。このことは、再生産関係としてホッケー・スティック モデルを用いる代わりに、制約条件(親魚量が8.5万㌧を超えた場合は、再生産成功率 × 8.5万㌧で、加入量を計算する)を用いることの科学的正当性がないことを示している。

従って、もし、「新しい水産資源の管理を実施した場合」の効果を検討するのであれば、図5に示したようなシミュレーションを実施すべきであり、図8で示したシミュレーションは、「新しい水産資源の管理を実施した場合とは異なる設定条件のもとで実施された意味不明のシミュレーション」ということになる。すなわち、図4に示されたシミュレーション結果から導かれた「新管理を実施することで、親は3倍、漁獲量も1.5倍」という結論は、「科学的正当性のない制約条件を付加することによって捏造されたもの」と言わざるを得ない。
以上のことは、現在、水産庁が強く推し進めている「新しい水産資源の管理」に関して、議論していく上でも看過できない重要な問題であると考えられる。図4は、本当に「新しい水産資源の管理」が適用された場合の結果であると見なせるのか否か、その真偽を明らかにする必要があると考え、公開質問状として、水産研究・教育機構にメイルで送付した、また、「note」の記事として、インターネット上に公開した。水産研究・教育機構からのご回答を是非インターネット上に公開していただくよう、お願いする次第である。
以下に、公開質問状の質問事項を整理した。
(1) 親魚量が8.5万㌧以上になると加入量が一定となるホッケーステック モデルを用いているが、親魚量が8.5万㌧以上になると加入量が一定になると仮定してもよい科学的根拠を示してほしい。
(2) 上記のホッケーステック モデルが科学的根拠のない単なる仮定であるならば、加入量が一定となる親魚量水準として、例えば、8.5万㌧の1.25倍、1.5倍、1.75倍、・・・、等の場合についても結果を示すべきだと思うが、そのような場合について結果を示す予定はないか? ないのであればその理由を説明してほしい。
(3) 新しい水産資源の管理のシミュレーションにおいて、ホッケーステック モデルを用いず、親魚量が8.5万㌧以上になった場合には、再生産成功率×8.5万㌧で加入量を計算することが、ホッケーステック モデルを用いることに相当するという科学的根拠を示してほしい。
(4) 2019年8月5日に水産経済新聞に発表されたシミュレーション結果について、その計算プロセスを詳細に記述した論文はどこかに公表されているか? その論文を教えてほしい。
(5) そのような論文が公表されていないとすると、なぜ、公表しなかったのか? 新聞にこのような結果を公表した場合、その影響力は極めて大きく、当然、その結果が導かれた計算プロセスの詳細を公表すべきであると思うが、それをしなかった理由をお聞きしたい。
(6) 結果が捏造されたものではないかという疑念に対する回答をお願いしたい。
9. MSY理論を用いると、漁獲量削減の効果が過小評価され、実際には不必要である過大な漁獲量の削減を実施しなければならなくなることは、5年前(2019年)に、既に、指摘されていた!
以上述べたゴマサバ東シナ海系群に対する分析は、3つのことを指摘している。まず第1は、MSY理論にもとづく資源管理が、漁獲量削減の効果を過小評価することになること(図5,図7)。第2は、図4に示した水産研究・教育機構が行ったゴマサバ東シナ海系群に対するシミュレーション結果(水産経済新聞2019年8月5日版)は、「もし、過去に新しい水産資源の管理を実施していたら?」というタイトルになっているにも関わらず、ホッケー・スティック モデルは使用されておらず、さらに、親魚量が8.5万㌧以上の場合は、科学的正当性が不明である「再生産成功率 × 8.5万㌧」によって加入量が計算されていること(図8)、第3は、極めて大きな漁獲量の削減が前提となっているにも関わらず、そのことについては明記されておらず、漁獲規制の効果だけが強調されていること(表1、図4)の3点である。
以上述べたことは、2019年8月5日の水産経済新聞の記事を見て、すぐに違和感を覚えた内容である。そのことを検討するために、急ぎ上で説明したようなシミュレーションを実施し、その結果を故・佐藤力生氏のブログ「本音で語る資源管理」の2019年8月22日版に掲載していただいたものである。しかし、最近になって太平洋クロマグロの資源管理の結果とも同根の問題があることが明らかになったので、改めて、本記事にも掲載することにした(ただし、シミュレーションの設定等は一部変更している)[9]。その2019年8月22日版のブログ記事の最後の段落を引用して、本記事の結びとしたい。
ー 2019年8月22日版のブログ記事の最後の段落を引用 ー
8.責任は誰がとるのか? 補償はどうするのか?
将来のことは誰にも分らないのは事実である。しかし、10年もすれば、どちらの主張がより妥当であったのかが明白になるだろう。もし、不必要に過大な漁獲量の削減を科していたことが明らかになったとき、そして、それが原因で多くの漁業者が、その時既に、廃業に追い込まれてしまっていることが明かになったときに、果たして、水産庁はどのような責任をとり、どのような補償を漁業者にするつもりなのだろうか? 水産研究・教育機構の研究者は、「我々は、ただ水産庁に言われたことを計算しただけです」と言って逃げを打つであろうから、責任を問われる心配はないかも知れないが・・・。10年後、全国各地でまき起こる訴訟の嵐の対応に水産庁は忙殺されることになるだろ。太平洋クロマグロでの管理の大失敗から、なぜ学ぼうとしないのか、不思議である。
ー 引用終了 ー
これはゴマサバ東シナ海系群に適用された「新しい水産資源の管理」のシミュレーション結果に対して、問題点を指摘した5年前のブログ記事の一節である。しかし、図らずも「不必要に過大な漁獲量規制を強行し、その結果、予定よりも13年も早く、たった8年で管理目標を達成することになってしまった」という太平洋クロマグロの資源管理結果の現状を、まるで予言しているかのような内容になっていたことがわかる。
ここで何が言いたいかというと、予言が当たっていたということではなく、「不必要に過大な漁獲量規制を強行し、その結果、予定よりも13年も早く、たった8年で管理目標値を達成することになってしまった」という太平洋クロマグロの現状も、決して、偶発的なものではなく、「最初から予想し得る必然的な帰結であった」ということである。なぜならそれは、「MSY理論に基づく資源管理が本来的に内包している致命的な欠陥の帰結であり、単に、それが現実となって現れただけのこと」であるからである。
太平洋クロマグロで起こったことは、他魚種でも起こる。そのことはゴマサバ東シナ海系群に対するシミュレーションで示したとおりである。これらのことは、水産庁が強引に推し進めようとしている、「MSY理論に基づいた、新しい水産資源の管理」が本来的に内包している致命的な欠陥を、明らかにしていると言うことでもある。
参考文献
1) WWFジャパン. WCPFC北⼩委員会会合2024閉幕 太平洋クロマグロ資源が安全⽔準まで回復 ネ イチャーポジティブの好事例に. 2024. 9. 3. 7
2) WCPFC. Assessment of Pacific Bluefin Tuna in the Pacific Ocean in 2024.
3) WCPFC-SC20-2024/SA-WP 08. 2024⽔産庁. 太平洋クロマグロの資源管理について(資料12). 令和6年9⽉
4) 水産庁. 令和元(2019)年度ゴマサバ東シナ海系群の資源評価. 水産庁HP.
5) Sakuramoto, K. Case Study: A Simulation Model of the Spawning Stock Biomass of Pacific. Bluefin Tuna and Evaluation of Fisheries Regulations. American Journal of Climate Change, 5, 245-260. 2016
6) 櫻本和美. ここが問題、新しい⽔産資源の管理-MSY理論に代わる新しい資源変動理論-.デザイン エッグ(株). 2020. 276pp.
7) 櫻本和美. MSY理論に代わる新しい資源変動の考え方. note 2023.12.11.
8) 櫻本和美. マグロ類資源の管理の成功に向けて―MSY理論に代わるべき新しい資源変動理論―. 水産振興605. (2018)
9) 櫻本和美. ゴマサバ東シナ海系群に対する水産庁の試算結果について. (2019. 8. 22). 本音で語る資源管理 | Topic of marine resource management
