
万華鏡の秘密(1)
今年は新型コロナウイルスの流行で,3月21日に予定していた東京ジャーミイでの万華鏡ワークショップは中止になってしまいました.申し込まれ方には次の機会にぜひと思っていますが,イベントをいつ開催できるかなかなか計画を立てにくい状況です.実施するときは皆さまにもお知らせします.
今年のとっとりサイエンスワールドは中止になってしまいました.
このような状況ですと,材料を配ってリモートで実施するというのも考えなければならないかもしれません.でも,ワークショップは現場でやりたいものですね.
■万華鏡の数学ー原理
(講義は,リモートでもできますね)
平行な合わせ鏡の間に置いた物体は,物体像と鏡像のペアが無限に繰り返す市松模様を生じます.2枚の合わせ鏡が平行でなくθの角度で交差する場合は,一次元の市松模様は円周に沿って並びます.円周の向こう側で市松模様がきれいにつながる条件は,360/2θ=n(整数)です.これは,万華鏡を発明した物理学者ブリュースターの特許(1817年)に書いてあります.

3枚鏡が3角形をなす場合は,3角形の各頂点でこの条件が成り立つので
1/n+1/m+1/p=1,(2=<n,m,p)が,平面がきれいな市松模様になる条件です.この条件を満たす3角形は図に示す3種類しかありません.
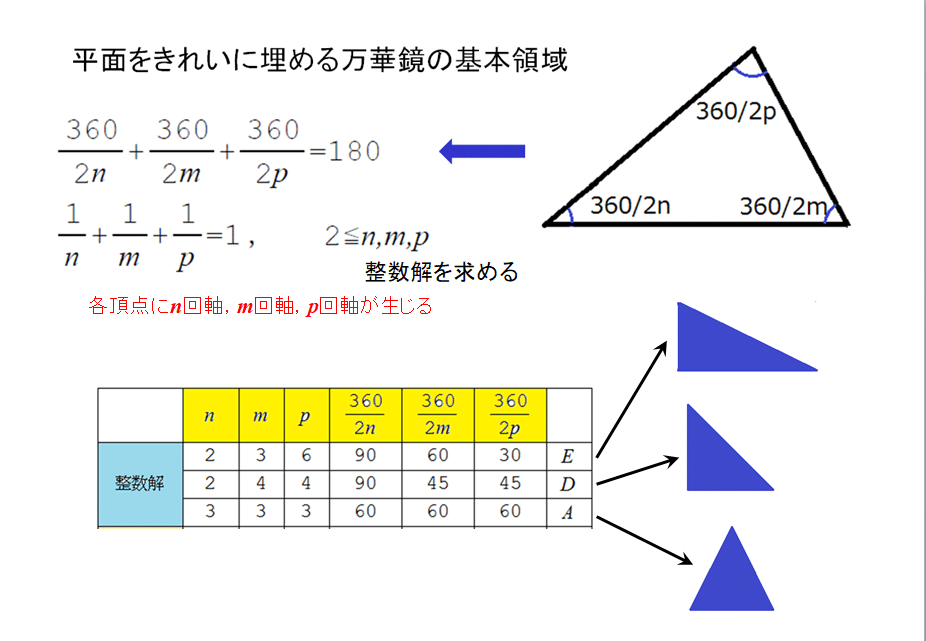

これだけではつまらないので,分数解も許すことにすれば,解は無限にあります.このような分数解の万華鏡は,平面の所々で市松模様が破綻しますが,やはり美しいものです.

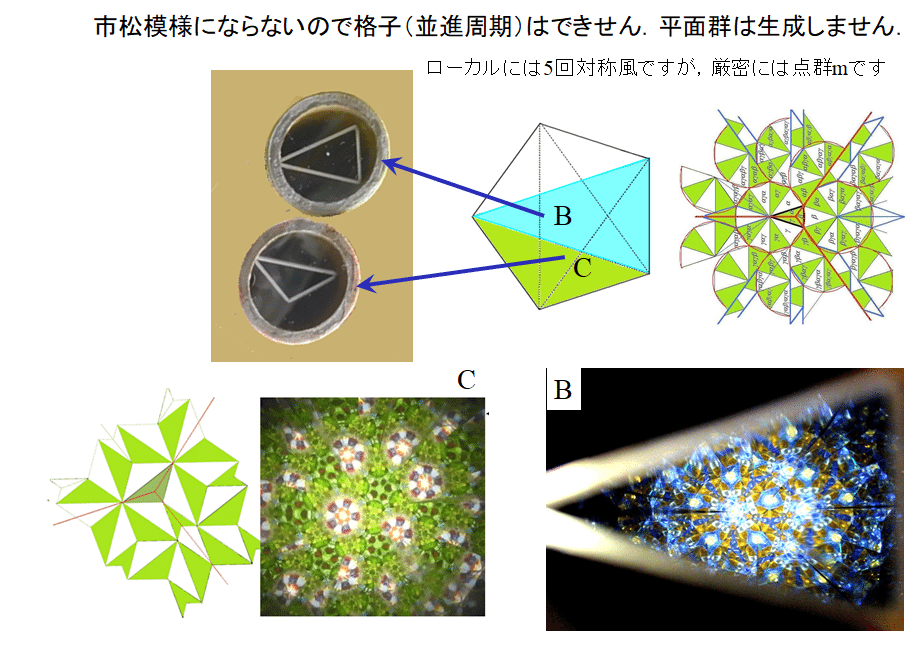
(参照)美しい幾何学,第5章
