230種の結晶空間群.結晶構造
結晶空間(=3次元の離散体)のブラベー格子は,14種類ある.ブラベー格子とは,結晶の内部構造の並進性とその対称性により,結晶構造を分類する概念である.
結晶空間は,無限に広がる3次元周期をもつ離散体(デジタル化された空間)なので,
①並進性(並進群で記述):並進で移動できる点(格子点)はすべて同価.
②格子点自体には,点群で記述される対称性がある.
結晶空間の全域に作用し,これを不変に保つ対称操作の集合が,その結晶空間の結晶空間群であり,結晶空間群の対称操作は,結晶点群と並進群の対称操作の組み合わせである.もちろん,並進群だけで結晶空間群の部分群を作る.結晶空間全域に作用し,結晶空間を不変に保つ結晶点群の対称操作は,当然,局所の格子点自体が従う対称操作でもある.
注)
並進群:3次元結晶空間には,互いに独立な基本並進ベクトルa, b, cがあり,その任意の1次結合n・a+m・b+l・cを格子点といい,すべての格子点の集合(無限集合)を格子という.格子は並進群の図的表現でもある.
結晶点群:結晶空間の対称操作(変換の前後で空間を不変に保つ操作)で,かつ,空間の1点を不動(特異点)にする対称操作の全体が作る群.
無限に広がる結晶空間で,並進で移動した位置はすべて同値(格子点はすべて同値)と考えると,無限個ある格子点を1点に還元でき,結晶空間群を結晶点群に還元することができる.
■石英,岩塩,ダイヤモンドの結晶構造の例.

低温水晶α-quartzの構造を観察すると,図面に垂直な3回らせん軸(風車のような記号)が,正3角形の格子点に分布しているのがわかる.これらの3回らせん軸は,1つの空間群のなかでは,すべて右まわりか左まわりに統一されている:空間群の記号でP3_{1}21(右),P3_{2}21(左).
石英の組成はSiO_{2}だが,この図に描かれているのはSiだけで,Si位置の紙面レベルからの高さを,黒丸,白丸,半黒丸で区別している.紙面に垂直方向の周期をc=1とすると,黒丸(+1/3レベル),白丸(-1/3レベル),半黒丸(0レベル)である.
紙面の矢印は,水平面内にある2回軸で,その高さレベルの数字が記されている.
ーーーーーーーーーーーーーーーーーーーーーーー

上図はNaCl結晶の単位胞を示す.Naイオン(黒丸)とClイオン(白丸)が,立方体の辺に沿って,あるいは,面の対角線や体対角線に沿って,交互に並んでいる.黒丸と白丸は,イオンの種類が異なるので互いに同価点ではないが,両者のペアは同価点になれる.例えば,白丸だけをペアの代表(格子点)と考えると面心格子Fになっていることが理解できる.
NaCl結晶構造の対称性は,並進(格子)だけではない.黒丸,および,白丸位置の対称性(点群)は,ともにm-3m(非座標記法では~6/4)である.この点群のステレオ投影図を,黒丸と白丸の位置に配置したものを上図に示した.NaCl結晶構造の空間群はFm-3mである.
-----------------------

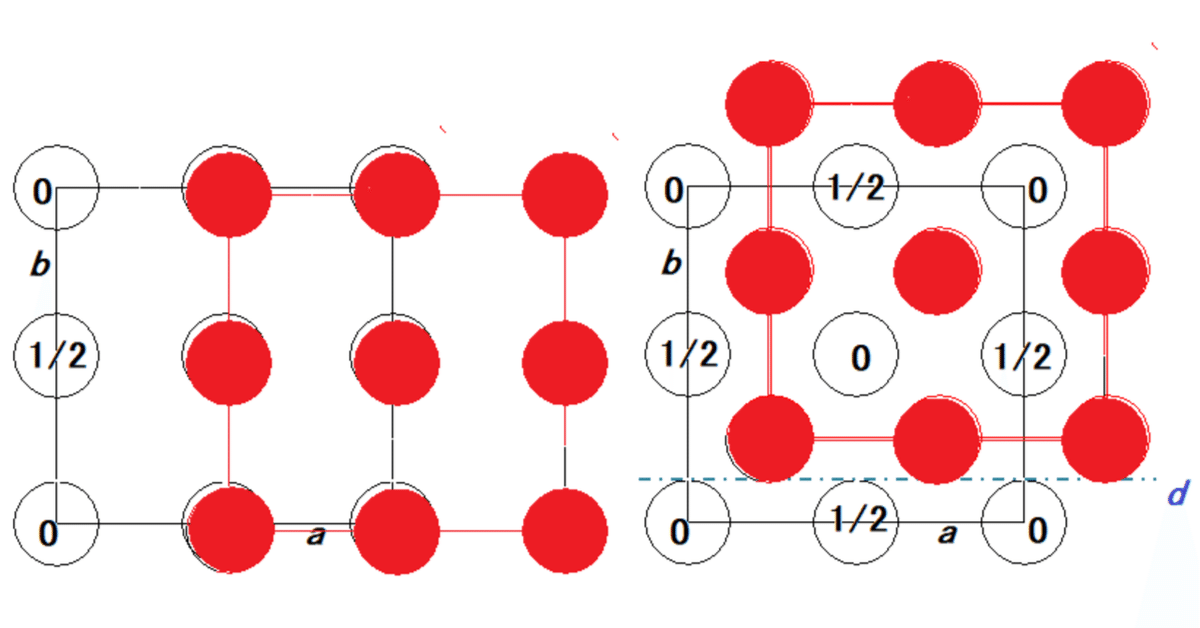
上図に示すのは,ダイヤモンドの結晶構造である.これは,2つの面心立方格子Fを,立方体の体対角線の方向に1/4だけ相対的にずらし重ねたものを考え,両方の面心立方格子の格子点に炭素原子を置いたものである.両方の面心格子の格子点をペアで代表点とすると考えれば,ダイヤモンド構造の格子は,面心立方格子Fであることがわかる.

2つの面心格子(黒と赤)は,例えば,映進面dにより互いに変換し合う.
黒の面心格子を,dで鏡映し,かつ,(1/4)a+(1/4)cだけ平行移動すると,赤の面心格子に変換され,この逆も成立する.ここで現れたdをダイヤモンド映進面と呼ぶ.
面心格子の格子点の点群は-43m=3/~4で空間群はF-43mであるが,ダイヤモンド構造では,2種類の炭素原子がこれらの2つの副格子の格子点を占めていて,ダイヤモンド構造の空間群はFd-3mである.
空間群Fm-3mとFd-3mには,共通な部分群F-43mを含み,点群m-3mとd-3m(格子を法とする点群)は,互いに同型な点群である.結局,空間群Fd-3mは空間群Fm-3mから,鏡映面mを映進面dに置き換えて得られる.
