球の表面積

半径Rの球の表面積は，４πR^2となることは知っていると思います．πR^2は半径Rの断面円(球の影)の面積ですから，球の表面積は，自分の影の面積の4倍になるわけです．なんだか不思議な気がします．
球の表面積を求めるには，円周が2πRsinθ，幅がRdθの円環（リング）に細分し，これを0≦θ≦πで積分すると，球の全表面積4πR^2を計算することはできます（図１）．しかし，計算してみてもつまらない．直感的に納得したいものです．

3Blue1Brownの動画はとてもよくできています．最後に動画のyoutubeリンクをおきますから後でご覧ください．見ているだけで楽しいです．教材にアニメーションを取り入れたいものですが，私はまだ作ったことがなく楽な方法をご存じの方はお教えください．

(図１）

球表面の円環を球の断面円(赤道の断面)に射影すると，円環の円周の長さ2πRsinθは，射影で変わりませんが，幅Rdθは，射影でRcosθdθになります．上半球の円環はすべて断面円内に射影されるので，断面円の面積πR^2を埋め尽くします．北半球（半球）の影は，πR^2sin2θdθを 0≦θ≦π/2の範囲で積分して，確かに断面円の面積πR＾2と計算できます．しかし，やはり積分の原理に戻り計算するのではなく，直感的に納得したい．

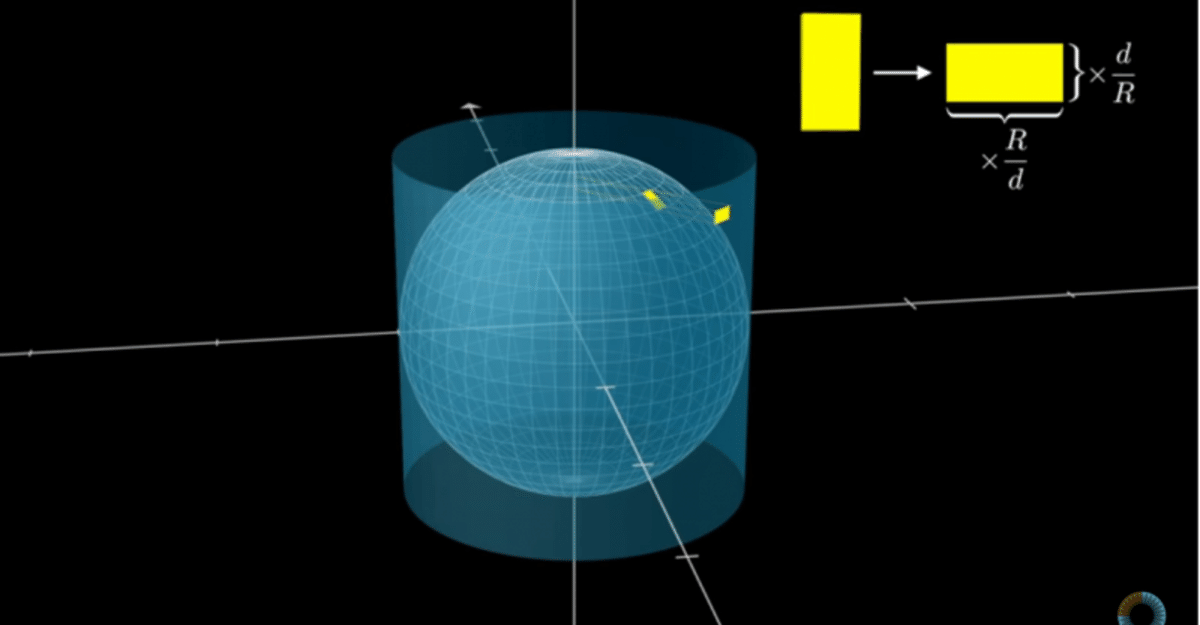
■（図2）は球を包むシリンダーをスクリーンにして，球を射影しています．

球の表面の微小な面積（緯線と経線で囲まれた矩形）を，球を包むシリンダーのスクリーンに，地軸に垂直平面に沿って射影すると，投影された矩形の縦横の比は変わりますが，面積は変わりません．このことから，半径Rの球の表面積は，幅2R（北極-南極），周囲2πR（赤道周り）の長方形（シリンダーの展開図）になり，その面積は4πR^2になることがわかります．
これは，積分の原理を使い（積分の計算はしない）直感的にわかるうまい説明です．

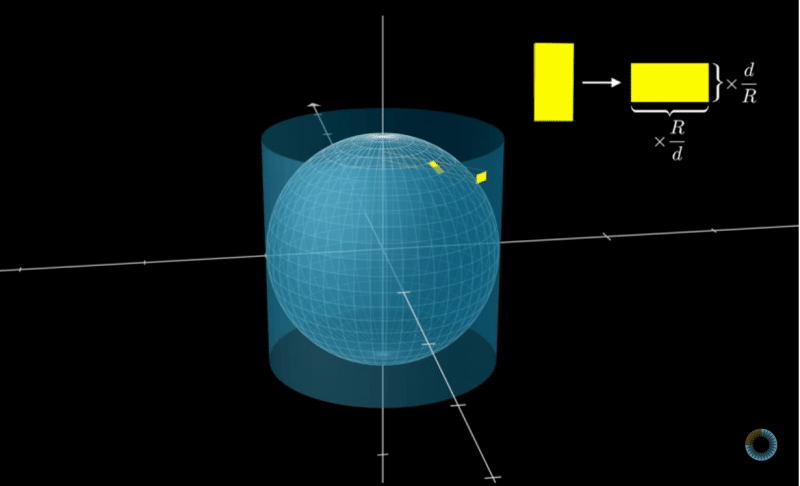
最後に，ぜひ3Blue1Brownのアニメーションをご覧ください．

https://youtu.be/GNcFjFmqEc8

一般に，正多面体の表面積と影面積（方位平均をとったもの）の比は4のようです．正多面体の極限としての球の場合は，表面積と影面積の比が正確に4になります．