虹の数学

■「虹の数学」を高校・大学で講義して，真島秀行（お茶の水女子大名誉教授）

数学月間企画講演第 4 回は 3 月 27 日(土)，15:00-17:00に，30名の参加者で実施しました．2020年度はすべてのイベントがZOOMによるリモート実施になりました．

講演者は，2002 年から，高大連携プロジェクト，教養基礎の一環として，「虹の数学」を，附属高校１，２年生に開設しました．これは物理と数学の授業と連携して実施され，種々の現象の理解に数学が関わっていることを体験させることが狙いです．虹シート（ビーズ）などの教材があり虹の実験も行えるとのことです．
講演内容の詳細は，数学月間HPにリンクがありますので，youtube動画や資料pdfをご覧ください．ここに掲載する短い記事は，数学が何をやろうとしているのかをわかる様に，物理の視点から書きました．数学の大海で迷子にならないように資料を読むガイドになると思います．
■幾何光学からの視点
虹の現象は，幾何光学による理解と，波動光学による理解とがあります．まず，幾何光学による基礎的な知識から理解できることは，主虹の外側に副虹（主虹より遥かに暗い）が見えることの説明です．筆者が作成した模式図をご覧ください．これで，主虹と副虹が生じる原理がわかるでしょう．
太陽からの光は散乱角180° −𝜑の方向に散乱されて目に届きます（𝜑は散乱角の補角）．

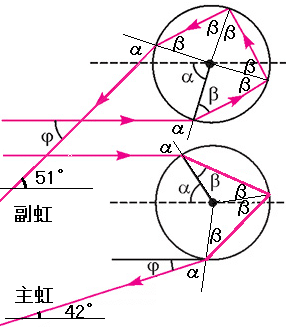
雨滴内部で１回反射して見える主虹の場合は，180°−𝜑＝180°−４𝛽+２𝛼，
2回反射して見える副虹の場合は，180°−𝜑 =360°−6𝛽+２𝛼で，
屈折の法則，sinα/sinβ＝n（水の屈折率は，可視光域で，n=4/3 に近い）を用いて計算すると，主虹と副虹の場合，それぞれ，角度𝜑 = 42°，𝜑 = 51°が得られます．しかし，目に届く光線はこのような角度𝜑だけに来るわけではありません．太陽からは平行光線が雨滴に入射したとしても，雨滴曲率のある球表面の入射角𝛼は変化します．そのため光線の経路は模式図のような1本ではなく，経路（「火線」と呼ばれる集光ライン）は拡がります．

角度𝜑を，入射光線の位置（雨滴の中心線からの変位距離）で微分して，その微分係数を0と置くと，「火線」と呼ばれる包絡線が得られます．幾何光学での説明はここまでです．幾何光学だけでは，主虹と副虹で色の配列順番が逆転することは言えても，波長による屈折率の変化（光の分散）を語るには，波動論の概念が必要です．
■波動光学の視点
色，位相，干渉などの現象は，本来，光の波動論で導入できる概念です．可視光の波長は，雨滴直径の1/1000程度で，球形の雨滴内を進む波面の形状を記述するには，光線の雨滴球への入射点や反射点が波源となる球面波の重ね合わせであるというホイヘンスの原理により，これらの素過程を重畳する必要があります．このような散乱光の波面（位相フロント）を記述したのがエアリーの功績です．雨滴から観測者までの距離は非常に大きいため，雨滴表面の位相面を波源とする球面波は観測位置ではほとんど平面波の重畳で，この電場を表すのがエアリー積分

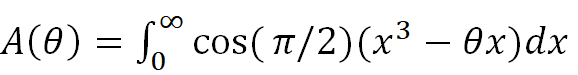
です．𝜃は「火線」のまわりの視角の外れ量に比例した変数です．エアリー積分𝐴(𝜃)は光線電場の振幅ですので，𝜃方向に観測される虹の強度は|𝐴(𝜃)|^2になります．空気が奇麗だと空気での吸収や散乱がないので，主虹のすぐ内側にかすかに色づいた過剰虹が観察できることがあります．過剰虹の現象は，このような光の干渉の効果のために生じるものです．
エアリー積分の数値計算を，テイラー展開を用いて計算すると収束が悪いために困難です．後に，ストークスはエアリー関数が解となる微分方程式を利用して，実数パラメータ𝑥を複素平面全体に拡げ研究しました．ストークスの研究は，𝜃が大きいときのエアリー積分の漸近挙動を調べる漸近解析へと発展しました．
虹の発生の解明の歴史は，幾何光学から波動光学への物理学の歴史でもあり，数学的にはエアリー積分から漸近解析への発展の歴史でもあり興味深いテーマです．