
曲線上または曲面上をまっすぐ歩くとは2
どこにも向きを変えずに直進し続けます。(バーバ・ヤーガ)
そして、私はまっすぐに行きます、左でも右でもありません...
(M.シュチェルバコフ)
ヴァレリア・シロタ「Kvantik」No.8,2020
AlexeyVayner(アーチスト)
ーーーーーーーーーーーーーーーーーーー
これで、どような地形でも「まっすぐ進み、曲がらない」とはどういう意味かがわかりました。これは測地線に沿った動きです。今、どんな表面に対しても、次の質問をすることができます:
1.その測地線はどのように見えますか?
2.2つの与えられた点を通る測地線を描くには?
一般的な場合、この問題は難しいので、円柱と円錐という単純な「ほぼ平坦な」表面を歩くことを提案します。
シリンダー
図4: シリンダー
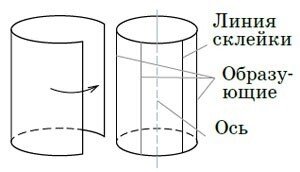
シリンダーを作るのは簡単です(図4):紙を1枚取り、それを筒に巻き、端を接着します(できれば長辺に沿って)。カブトムシをその上に乗せて、それが這うように測地線を描くことができます。
最初から接着線に平行な方向を選択すると、カブトムシはこの線(および円柱の軸)に平行な直線に沿って這うようになります。このようなラインはジェネレーターと呼ばれます。軸に垂直な方向に移動を開始すると、測地線は円になります。
チャレンジ問題 斜めなど、他の方向に進むと、どのような線が表示されますか?
円錐
図5 円錐
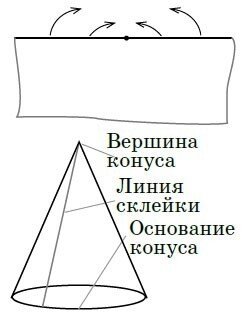
すぐ作れます。接着も簡単です。最も簡単な方法は、大きな紙を取り、その側面の1つの点を選択し、この点で区切られた側面の2つの半分を接着することです(図5)。円錐の底面が不均一で、角が突き出ていても問題はありません。実際の円錐面は無限であり、これはほんの一部であると見なすことができます。
問題 この表面で測地線はどのように見えますか?
