イマジナリーキューブのパズルと数理

第8回数学月間企画講演会(2021.10.23)　立木秀樹（京大）

イマジナリーキューブとは，直交する3方向（立方体の３方向の辺）に沿って見る（射影する）と，立方体と同じに見える立体のことで，図に示す正4面体や，HとTなどの立体があります，HとTは，立木氏が開発したイマジナリーキューブ・パズルで現れる立体です．

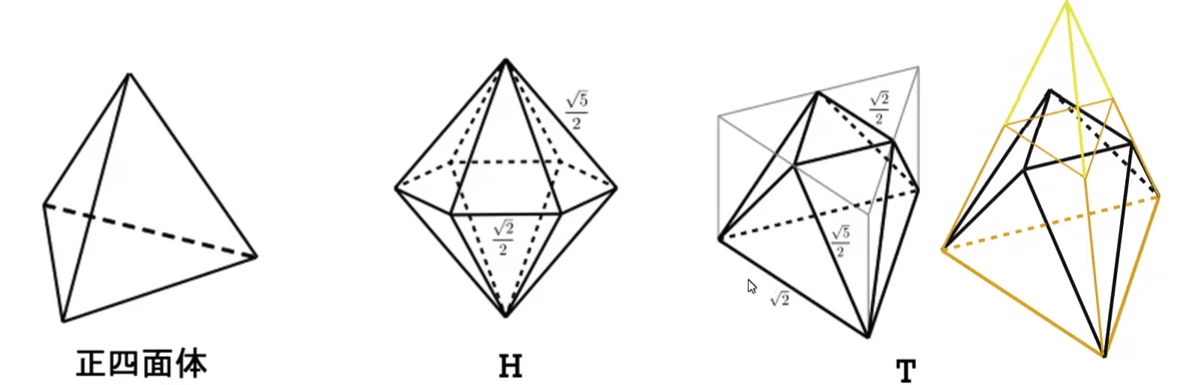
HもTも1辺１の立方体に入るイマジナリーキューブとすると，1辺２の箱の中に8つのイマジナリーキューブが収まるのは当然ですが，3個のHと６個のTのイマジナリーキューブ計9個を収めるのがこのパズルです．これは，面と面を合わせて空間充填された状態で詰め込まれます．４つのTの頂点が集まる位置にできる窪みにHが突き刺さるように入り，Tの層に挟まれてHが入り，この構造での個数比はH:T=1:2です．空間群でいうとP6/mmmの積層構造になります．無限に続くこの結晶構造から1辺２の立方体の箱に収まる部分を切り取るのは，3回回転対称軸を立方体の体対角線に一致するようにすると得られます．

このイマジナリーキューブの発想は，フラクタルから生じました．イマジナリーキューブ立体図形をフラクタル配置で拡げたものは，やはりイマジナリーキューブになることが，数学的帰納法で証明できます．正4面体から作ったシェルピンスキー4面体（シェルピンスキー・ガスケット）は，やはりイマジナリーキューブであり，Hから作ったフラクタルもTから作ったフラクタルもイマジナリーキューブであります．これらをイマジナリーキューブの辺方向から少しずれた方位で投影した図には，大変美しい形がときどき見られます．3Dプリンターでこれらのフラクタル模型を作ったり，また，正4面体を集めてシェルピンスキー4面体の工作をし，大学から中学までの各レベルの数学学習に合わせて活用しました．数学的帰納法は級数で導入するのが普通ですが，フラクタル図形で導入するのも自然で理解し易いようです．正4面体のイマジナリーキューブ・フラクタルの京大オブジェや，フラクタル日除けを作りました．フラクタル日除けは，日除け自体の熱容量が小さいので熱を貯めないなどの利点があり，酒井敏教授（人間・環境学研究科）がキャンバスに建設しました．太陽光線による影が，イマジナリーキューブになるという特定方位の瞬間は，実際にはないが，フラクタル木漏れ日は気持ちの良いものだそうです．