
球の密な充填
結晶学と構造工学における重要性
(解説)
3次元空間で球の最密充填(ケプラー予想)は肯定的に証明されましたが,この予想の証明は難問でした.ここでは,最密であるということには敢えて踏み込まず,高密度充填(実は最密充填)というにとどめます.さらに証明は省いて,ここで考察するのは球の充填ではなく,球の最密配列層(シート)の積層の様式として,最密構造が得られるとします.
球の最密充填構造は,パチンコ球をトレィに並べたときに見られる最密配列シート(層)を積み重ねて得られるものであることは,結局,正しい結果でしたが,厳密な証明はとても難しいようです.
教科書に出ている立方最密充填と6方最密充填はよく知られていますが,3種類の層の積層様式から作れる多型は無限に作れます.
現在,離散体の対称性は,結晶学や固体物理学で関心を持たれていますが,その理由は,すべての結晶は離散体であるからです(結晶は連続体ではなく,原子で構成されています).
離散体の対称性は,他の学問分野や工学分野からも少なからず関心が持たれています.特に,建築美術は,これまで空間的な構造を計算する方法を知らなかったため,「平面的な問題」を解決する段階にとどまっていましたが,離散体の対称性理論が,すでに建設工学にも応用されています.例えば,レンガや積みやトラス構造などに関係があます.隙間や重なりなく平面を分割する方法,球の最密充填の方法は,N.V. Belov(1947年)とToth(1953年)の研究に学びます.
一見,球を高密度に詰め込む方法は1通りしかないように見えますが,実際には無限にあります.これを理解するために,同一の球を,それぞれの球が6つの球に隣接するように層(平面)に並べてみましょう.この配置は平面で最密配列であることは証明できます[パチンコ球のをトレィに並べた様子を思い浮かべてください].第2層の球は,第1層の上に配置し,これも同様に最も密であるように配置することができます:
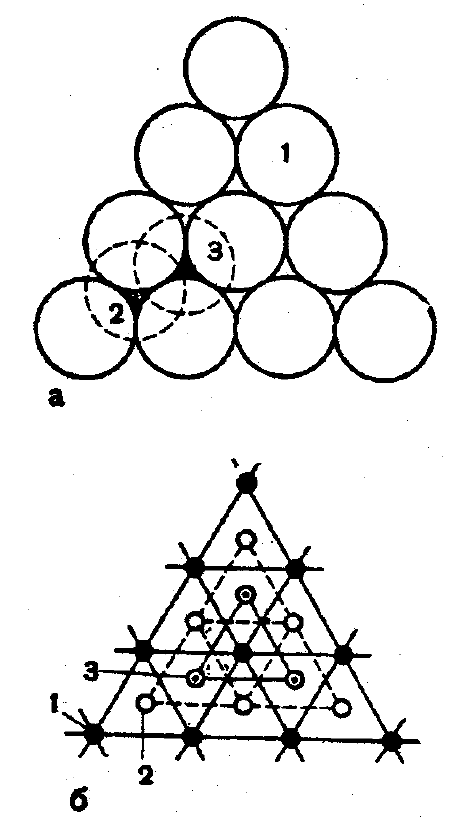
第2層の球の 1 つは,第1層の位置2番または位置3の窪みを占めることができますが,どちらを占めても同じ結果になります.第3層を,出来上がった2層系の上に積み重ねるには,2つの方法があります:第3層の球を,第1層の球の位置に置くか,第2層の球が位置2を占めていれば,位置3に置くかです.このようにして得られた2種類の3層系の違いは,第3層の球を投影した時,1番目の層の球と一致するか/しないかにあります.
球の中心を平面に投影すると,どの層に対しても,投影で示された球の位置は,3つの位置以外に存在しえないことがわかります.したがって,球の最密充填は,数字の1,2,3からなる記号で表すことができ,これらの数字の有限または無限の列のなかで,同じ数字が2つ続かないようにします.明らかに,この条件を満たす3つの数字の配列様式は無限です.したがって,球の最密充填は無限にあります.無限に続く数字の列が,ある同一の有限の組み合わせを周期的に繰り返すならば,それは対称的な離散体であることになります.そうでなければ,同じように球を高密度に積み重ねても,少なくとも層に垂直な方向は,非対称な配列になります.例えば,12312 12312 12312....は,12312という組み合わせが周期的に繰り返されていることから,対称的(周期的)な5層構造と定義されます.この列の2つの数字の間に,少なくとも1つの余分な数字を挿入すると,構造の並進対称性が一気に崩れます.
対称的(周期的)な積層において,すべての球(半径が等しい)は,構造中の占める位置に関して互いに同等ではないことに注意しましょう(同等性は3層構造の場合にのみ当てはまります).多層構造のすべての球には,構造のすべての層ではないが,異なる層にある並進同価な球の無限集合があります.非対称な積層では,同じ球は同じ層の同じ位置にしか入りません.
球の最密充填は,どのような対称群になるのでしょうか.対称的な積層に対応する数字の配列を調べましょう.数の配列が,左から右に読んでも、右から左に読んでも同じなら,構造には層平面と一致する対称面が存在することになります.例えば,列1213121312.....では,対称面は層2と層3を通過しています.もし,順方向と逆方向の読み取りで,数の並びが違って見えるなら,構造に対称面はありません.層面の対称面を持つすべての構造は,同じ6方対称(P6_{3}mmc)です. 例えば,6方対称の二層積層12は,このような対称性です.

実線の3角格子は第1層,破線の3角格子は第2層.
実線円は第1層の球,破線円は第2層の球.
対称要素と球の積層構造の投影図を重ね合わせ,第1層の球を実線で,第2層の球を破線で示します.第1層から第2層への変換は,紙面に垂直な螺旋軸
6_{3}と2_{1}(これらの投影は軸を,それぞれ羽付きの黒い6角形とレンズで表示),反転(紙面からc/4上にある白丸),並進c/2を伴う垂直な映進面(破線で表示)が担います.これらの要素に加えて,この投影図には,垂直方向と水平方向の対称面が描かれています(後者は第1層の球の中心と一致しています).水平な対称面間を通過する水平な2回軸は,投影図には表示されていません.

(図2c)下図は立方対称の球の積層Pm¯3m
(図2b)
水平な対称面を持たない球の配列(立方体の3層配列を除く)は,すべて3方対称を持ちます.例えば,12132の3方対称の5層積層は,空間群が
P¯3m1です.投影図の各層1,2,3の球は,それぞれ長短の点線と実線で表しています.
第4層の球は第1層の球と,第5層の球は第2層の球と,投影が一致しています.紙面上にある対称心(小さな白い円)は,第3層の球の中心と接点に一致しています.同じ中心で,第4層の球(紙面上)は第2層の球(紙面より下)に,第5層の球は第1層の球に映されます.
この投影図には,対称心のほかに,垂直方向の対称面(実線),映進面,垂直方向の単純軸3と回反軸¯3が示されています.水平方向の対称軸2, ¯2は,投影されていません.
(図2c)は,立方面心格子の対称性を持つ3層構造の投影図ですFm¯3m.図cとは対照的に,このグループの対称要素は,垂直軸3に沿って図面上に投影されており,点群m¯3mのステレオ投影の中心は,球の中心と一致しています.第1層の球の中心は紙面の中心にあります.第1層の球から第2層および第3層の球(図中に数字で示されている)への変換は,垂直な螺旋軸3_{1}, 3={2}
で回転させることによって行うことができます(それらの投影は,羽付きの小さな黒い3角形で示されています).また,対称心(レベルc/6およびc/3
の小さな白い円)で反射させることもできます.第2層と第3層の球の中心は,投影図に対応する数字で示されているように,レベルc/3と2c/3にあります.さらに,この投影図では,レベルc/2にある対称心が,第2層と第3層の球と映進の垂直面を結んでいます.群Fm¯3mの対称要素の一部は,投影図には表示されていません.

立方および6方の高密度充填の3次元モデルを図3a,bに示します.
2層積層では、位置3(図1参照)が球で占められていないので,層に垂直に走る構造的なパイプ溝が,6_{3}のらせん軸に沿って走っている.
立方積層には,構造上の溝はありません.
この両者の積層様式は,ほとんどの化学元素の結晶構造や,多くの無機化合物や鉱物の構造に見られる陰イオンの積層構造に対応しています.
