正12面体の見える万華鏡をつくろう

正12面体や球面正12面体は，正５角形（あるいは，球面正５角形）の面12枚が囲んでできる立体です．
3枚鏡の組み合わせで万華鏡を作り，正12面体や球面正12面体が見える万華鏡を作りましょう．
正12面体の点群（対称性）を生成する3枚の鏡に，次のものを選びます．
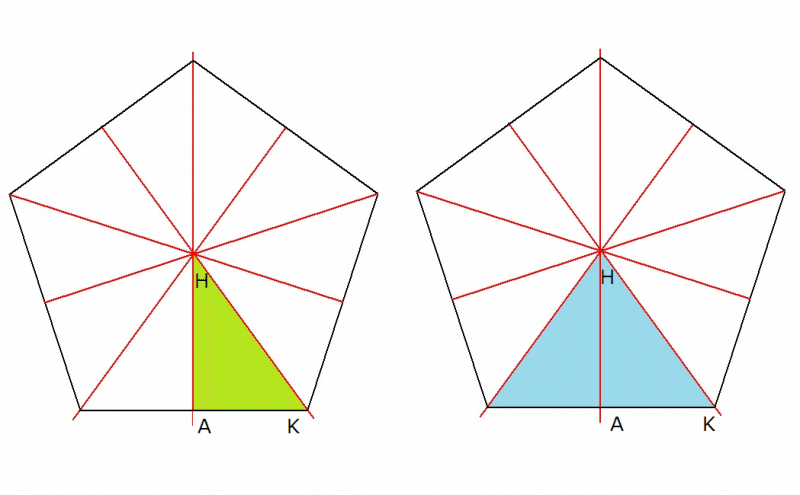
（Aタイプ）１つの正5角形の面を10個の直角3角形（若草色）に分割し，
その領域を立体の中心から見込む「3角錘」が万華鏡になります．
（Bタイプ）１つの正5角形の面を５つの2等辺3角形（水色）に分割し，
その領域を立体の中心から見込む「3角錘」が作る万華鏡になります．

（Aタイプ）　　　　　　　　　　　　　　　　　　　（Bタイプ）

作製したそれぞれの万華鏡で見られる映像を対応させて掲載します．
どちらも正12面体の映像が見えますが，両者の正5角形の面を観察して比較しましょう．
Aの映像では直角3角形10個で正5角形の１つの面を作っていますが，Bの映像では2等辺三角形5個で正５角形の１つの面を作っているのがわかります．

■正12面体および球面正12面体の見える万華鏡（Aタイプ）の作り方

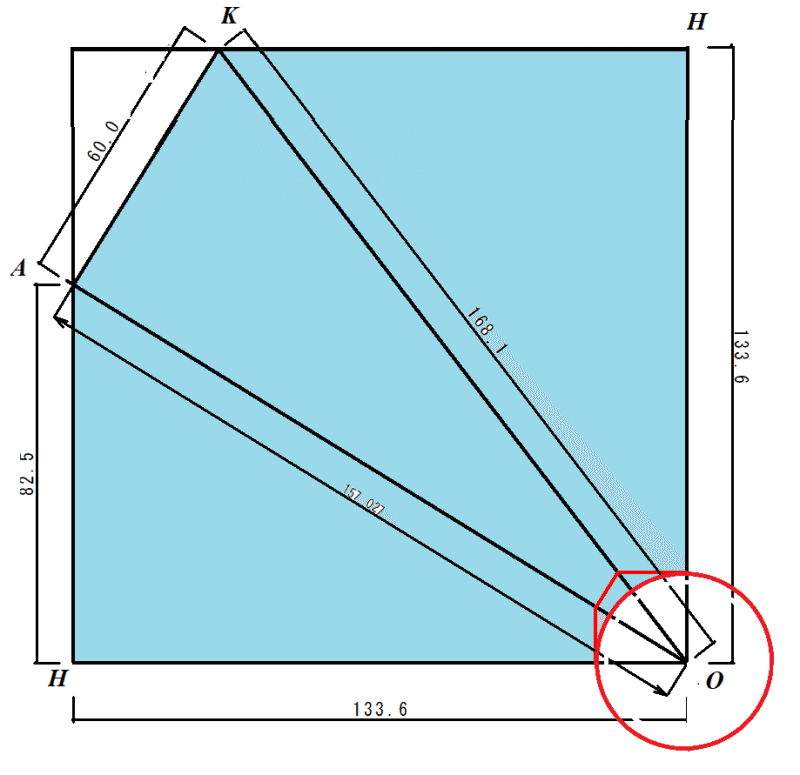
ミラー紙（厚さ0.25mm以上が良い）に次の展開図を描きます．青色の部分を使います（赤線に沿って光の窓を作ります）．赤線の円に沿って切ると「球面正12面体像が見える光の窓」，赤線の直線に沿って切ると「正12面体像が見える光の窓」ができます．どちらかを選びます．辺OHが共通につながるように3角錐（鏡面は三角錐の内側）を組み立てます．完成した万華鏡は△KAHから覗きます．

「美しい幾何学」球面正多面体とメビウス万華鏡p.133~p135に，この万華鏡の説明があります．

美しい幾何学