
Penrose タイリングから単一タイルによるタイリングまで
ここで対象とするのは2次元ユークリッド空間(平面)に限りましょう.2次元世界は厚みのない世界,つまり表面だけの(裏表のない)世界です.
2次元平面のタイリングとは,1種類(Penroseタイリングでは2種類)のタイルで,隙間も重なり合いもなく,平面を張り詰めることです.
結晶内部の原子的構造は,単位胞と呼ばれる単位ブロックがあり,これが面と面をピッタリ合わせて積み重なり結晶全体ができています。例えば,直径3.5mmのダイヤモンドの内部構造は,単位胞が$${10^7}$$個も並んでおり,事実上,単位胞が無限に繰り返す世界になっています.結晶空間とは,このような周期的な空間のことで,単位胞を点と見なすならば,結晶空間は周期的な点集合(=格子),つまりデジタル化された空間といえます.ここで,今,対象としている2次元に限定すると,2次元の結晶空間(周期的平面)の単位胞は,平行4辺形あるいは平行6辺形でなければならないことがわかります。逆に考えて,何らかの形のモチーフタイル(構造単位,敢えて単位胞とは言わない)があり,このタイルで平面をタイリング(平行移動だけでなく,回転移動も許す)できれば,必ず,周期な構造になるかといえば,そうとは限りません.すぐに反例が見つかります.
■非周期だが均一でないタイリング
図1は,1936年に Voderberg が示した奇妙なタイル張りです.これは1種類の9辺形のモチーフタイル(カニのツメのよう)だけでできていて非周期です.この構造の特徴は,2つの特異点があることです.これを単純化した非周期タイリングも示しておきましょう図1(右下).

■凸多角形(3,4,5,6角形)タイリング
1つの多角形による平面のテッセレーションで,パズルのように思いもつかないようなパターンを考案した例がいくつか報告されています.
例えば図2のパターンは,1つのモチーフ6角形タイルで,平面全域を均一にタイリングしていますが,決して非周期パターンではありません.

凸5角形によるタイリングに関しては,1975年のガードナーのコラムに,ラインハルト(1918年)の5タイプと1967年にカーシュナーが発見した3タイプの計8タイプが掲載されていました.ところが新しいタイプがまだあったのです.主婦マジョリー・ライス(フロリダ州生まれ)は,1975年の Scientific American 史のマーチン・ガードナーのコラムを見てこの問題を知り研究し自分の仕事をガードナーに送りました.ガードナーはそれをペンシルバニアのモラヴィアン・カレッジのタイリング問題の専門家であるドリス・シャトシュナイダーに送ってくれました.シャトシュナイダーは,彼女の発見が正しいことを確認したのです.彼女が発見したのは,張り詰め可能な4つの新しい凸五角形タイプです (1977).1975年以降にマジョリーの4種を含む計7種が発見されて,全部で15種類が発見されました.最後に発見 (2015) された15番目は,やはり周期的(単位胞が12個の5角形で構成される)なようです(発見にスーパーコンピュータが使われました).
■Penroseタイリングの登場
Penroseタイリングは,これら2種類の例とは全く異なる性質があり,2次元平面全域を,非周期に,均一にタイリングすることです.Penroseタイリングの源流はイスラムのモザイク模様にも見られます.Penroseタイリングの特徴を一言でいえば,フラクタル構造で出来上がっていることです.
2種類のタイルの内部を再分割したあとで$${\phi=(1+\sqrt{5})/2=1.618\cdots}$$倍拡大すれば,始めのパターンと同じものが見えます.この操作はInflationと呼ばれます.同じことですが,2種類のタイルを組み合わせたパターンを作り縮小すれば,始めのパターンと同じものが見えます.この操作はDeflationと呼ばれます.このようにしてできるパターンはフラクタル構造です.
ロジャー・ペンローズが考案した(1966)ペンローズ・タイリングは,
2種類のタイルによる規則的ではあるが,周期的ではないタイル張りの
一つです.



■ 1種類の形のタイルによる非周期タイリング
ペンローズタイリングは,2種類の形のタイルを用いている.1種類の形のタイルで非周期タイリングが可能でしょうか.これを「アインシュタイン問題」という.(ドイツ語で「タイル1枚」をein steinという)
結局,1種類の形のタイルを用いた非周期タイリングは可能でした.
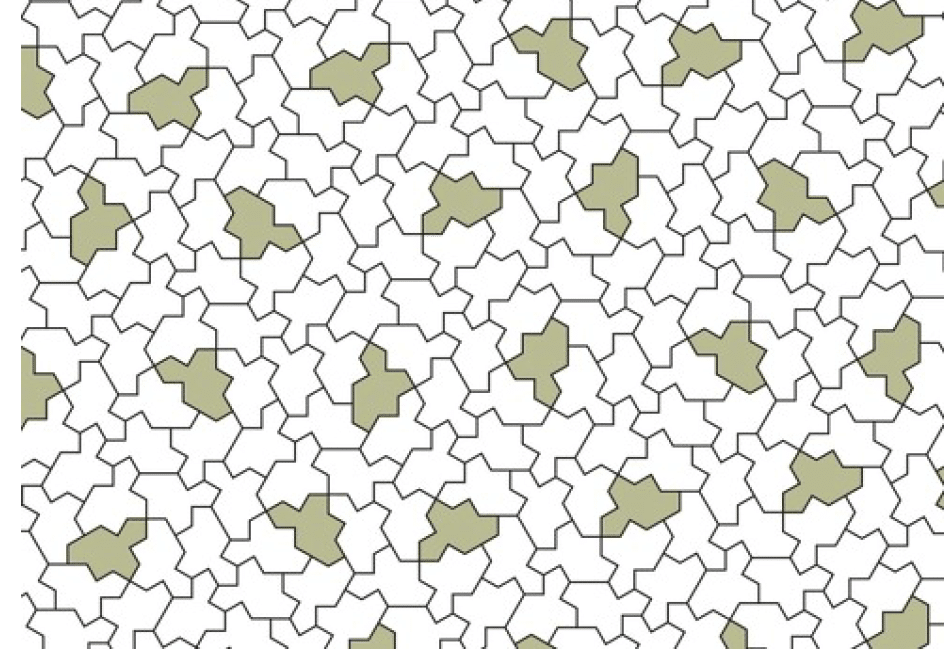
以下の2種類の非周期タイリングは,2023年にDavid Smithらにより発見されたものです.これらが非周期であることを確認するのは容易いことではありません.

ただし,濃青タイルと(薄青&白)タイルとは,互いに鏡像(裏返し)になるので,2次元平面で1種類のタイルとは言い難い.

引用
1.美しい幾何学(谷克彦);技術評論社;p68~70, p76~80
2.A chiral aperiodic monotile;David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss;(2023)
