星型多面体★

■ 星型正多角形（ダ・ビンチの星型）
　下の青や緑の図形は，星型正多角形の例で星型５角形（五芒星）と星型８角形（ダ・ビンチの星型）です．頂点同士を結んだ赤い輪郭線は，それぞれ正５角形と正８角形になり，凸多角形（凹所のない多角形）です．星型自体は，星状凸集合（領域内の点で，そこから領域内の任意の点を見通す線分がすべて領域内に収まるような点が存在する集合）ではあるが，凸多角形ではありません．

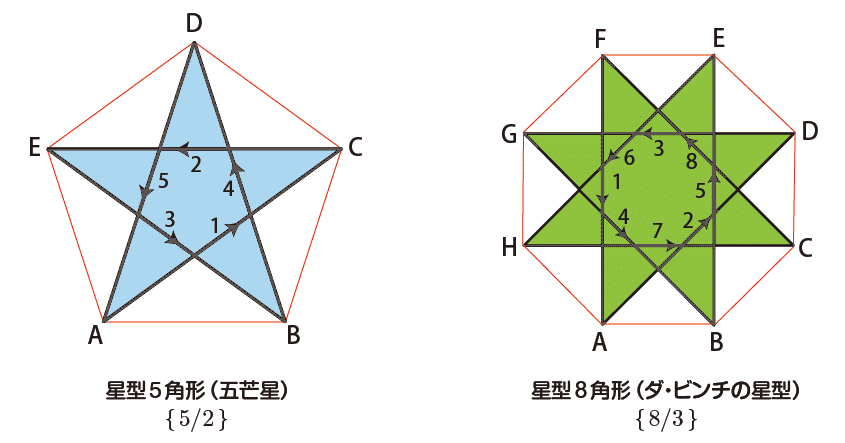
　青い星型５角形について詳しくみていきましょう．頂点Ａから辺をＡ→Ｃ→Ｅ→Ｂ→Ｄ→Ａと１周りたどると，辺の向き（→）が２回転することがわかります．あるいは，「５角形の頂点を１つ飛ばしでたどって，２周して始めの頂点に戻る」という言い方もできます．このような星形を { 5/2 } と表記します．
　星型８角形（ダ・ビンチの星型）でも同様で，右の図形は { 8/3 } です．

星型５角形を 5/2 と書くのは，2×360˚/5=360˚/(5/2) だからです．この星型５角形が頂点で５つずつ集まる { 5/2, 5 } は，星型小12面体になります．

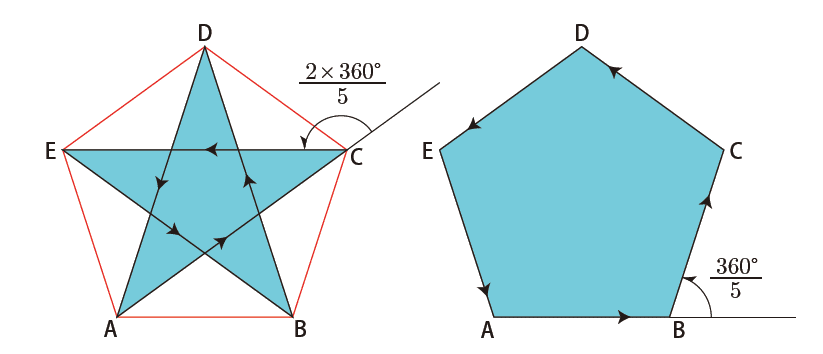
■星型正多面体（ケプラーの星形正多面体より）
（1）正12面体をコア（芯）にしてできる星型「星型小12面体」
　右の写真の星型は，東京都庭園美術館，旧朝香宮邸，姫宮の部屋の照明器具にも使われています．
コアになるのは正12面体で，その12個の正５角形の面の上に，それぞれ正５角錘を取り付けた形をしています．正５角錐の頂点は，それぞれ，芯となる正12面体の面に対応していますから，頂点を結んでできる図形（赤の多面体）は，正12面体に双対な正20面体です．

これは，正５角錐の頂点（例えばA）の周りに，星型正５角形 { 5/2 } の面が５個集まっている立体です．芯に正５角形の穴のある五芒星の板を，各頂点で５枚ずつ組み合わせると，この立体になります．したがって，この星型正多面体はシュレーフリの記号で { 5/2, 5 } となります．
　さて，この星型小12面体 { 5/2, 5 } は，プラトンの正多面体（正12面体）を芯にして，その正５角形の面に正５角錐を貼りつけた形（正5角錐の側面は芯の正12面体と同一平面にあります）でした．同様に，プラトンの正多面体（正20面体）を芯にして，その正３角形の面に正３角錘（正４面体）を貼り付けてできる形は， 星型大12面体{ 5/2, 3 } と呼ばれます．これら２つの星型は，ケプラーの星型多面体とも呼ばれます．序に，この２つの星型に双対な，{ 5, 5/2 }，{ 3, 5/2 } は ポアンソの星型と呼ばれます．
　星型小12面体は，五芒星の面F が12枚，稜の数E が30，頂点の数V が12ですので，F−E+V= −6（ 私たちの知っているオイラーの多面体定理では２）となります．これは星型小12面体の空間が，球の位相と異なり，穴が４つ空いた浮輪と同じ位相であるためです．（穴が１つ開くごとにF-E+Vは２づつ減ります）

美しい幾何学，p152-154

美しい幾何学