正多面体

正多面体の対称性は，中心に特異点を（点群）もちますが，特異線はありません．正多面体の対称性を持つ図形では，各軸はそれと等価な複数の軸を持っているので，どの軸も特異軸となり得ません．正多面体のリストから球を除外すると，これらの図形の対称性は，次の３つの点群に還元されます．
［~4，~6，~10の~は，数字の上に乗せて表示し，回映軸を意味します．］
　3/2･m = 3/~4 　　　~6/4＝3/4･m 　　　　　　　3/5･m = 3/~10 　

それぞれの記号には，その対称性の代表として，5つの正多面体（プラトン立体）；｛４面体｝，｛立方体，8面体｝，｛正12面体，正20面体｝を掲載しました．引用する図は，「美しい幾何学」p.9，16～19からです．

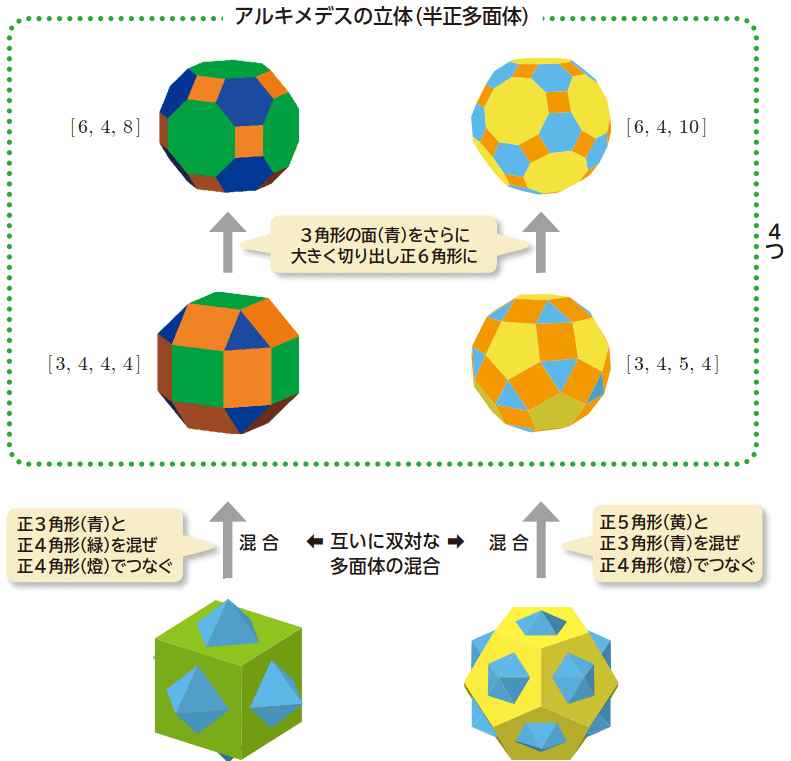
５つの正多面体のうち，正6面体と正8面体を重ねた立体の図がありますね．この図形の両者は互いに双対（面⇔頂点を入れ替えた図形）と言います．
同様なことが，正12面体と正20面体を重ねた立体の図でも言えます．つまり，正12面体と正20面体は互いに双対な立体です．互いに双対な図形の対称性は同じです．

正多面体の３つの対称性から，対称性を落としていくと，それらの部分群も導けて，結局，全部で７種類の点群を導くことができます．

美しい幾何学