多面体の見える万華鏡

多面体の見える万華鏡をつくりましょう．

reciprocalという言葉があります．経済などでは，互恵的とか対等とかいう意味で使われます．結晶学では，結晶格子crystal latticeに対して，逆格子のことをreciprocal latticeといいます．
両者の関係は，多面体でいうと，面を頂点に，頂点を面に変換した多面体
（これを双対dualな多面体という）の関係と同じです．

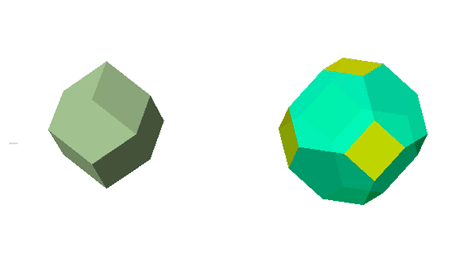
例えば，シリコンの結晶格子は面心格子で，ディリクレ胞を描くと菱形12面体（左図）です．シリコンの逆格子は体心格子で，ディリクレ胞を描くと［6,6,4］半正多面体［いわゆるケルビン立体］（右図）です．

結晶格子中のデリクレ胞と逆格子中のデリクレ胞は，このように互いに双対です．格子latticeに対して逆格子reciprocal latticeとはうまく名付けたものです．
もちろん，対称性はどちらも同じ，正6面体（角砂糖）と同じ対称性です．菱形12面体と［6,6,4］半正多面体（ケルビン立体）の形が見える万華鏡を作りました．この万華鏡は，左から覗くと菱形12面体が，右から覗くとケルビン立体が観察され，両者の対称性は同じであることを理解するのに役立ちます．

ーーーー

(注）用語（ディリクレ胞，格子，逆格子，面心格子，体心格子，半正多面体）は，説明なしに用いたので，別の機会に補足説明をいたします．

参考　「美しい幾何学」　　今，試し読みができるようです．
p.44～ 45　万華鏡で作る多面体
p.60～ 62　ディリクレ胞，格子

美しい幾何学