コペルニクスの定理またはロボット掃除機

クバンチク12月号(2016)p.2～6に，S.Dorichenkoによる表題のエッセイがあります．冗長ですので，図は用いていますが，独自の説明にしました．

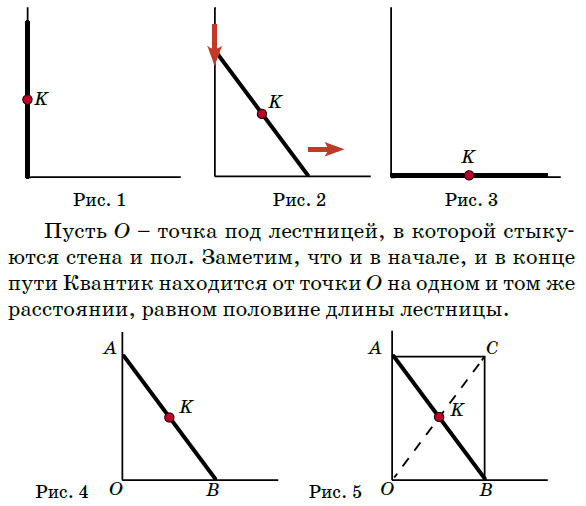
梯子が壁に沿って立っている状態（図1）．Kは梯子の中点でここにクバンチク君がいます．梯子の上端が壁に沿って下にスライドし，下端が床に沿って右に移動します（図2，3）．クバンチク君の描く軌跡は？

壁と床の交点をOとすると，クバンチク君の位置KはOからの距離が常に等しい（梯子の長さの半分）ことに注意しましょう．

従って，クバンチク君の軌跡は中心Oとする半径OKの円（青い線の全円周の1/4）．

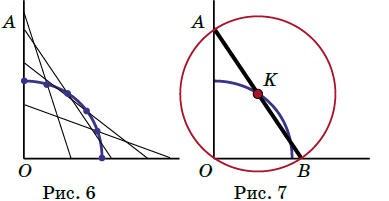
Kを中心として直径ABの円（赤い円）を考えます．Oは円周上にあります．
Kが青い円の上を運動するとき，赤い円の直径ABの端点A及びBは直線運動をします．

■赤い円と緑の円があります．緑の円の直径は赤い円の2倍です．赤い円は緑の円の内部から内接し，接点は滑らずに緑の円に沿って回転します．
始めの図は，赤い円の直径ABのA点が緑の円のN点に，赤い円のB点が緑の円のO点に一致している状態です．緑の円の内部で赤い円が滑らずに回転し，C点が接している状態になったところが次の図です．
A点は縦軸上を移動し，B点は横軸上を移動することがわかるでしょう．この調子で，赤い円の中心Kが右回りに回転を続けても，A点，B点はそれぞれ直線運動を続けます．これは，回転運動を直線運動に変える機構に利用できます．

コペルニクスの定理
円が，直径2倍の円の内側に沿って滑らずに回転する場合，回転する円周の各点は，必ず，原点Oを通る何らかの直線上を運動をします．

■ロボット掃除機の動き
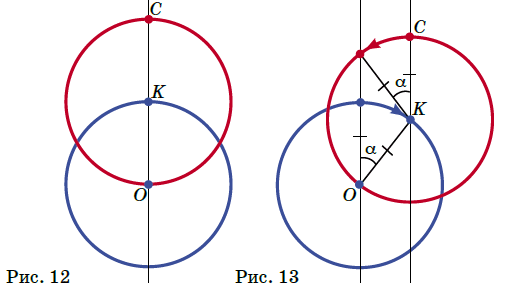
赤い円をロボット掃除機とします．ロボット掃除機の中心Kが青い円に沿って動く．掃除機自体が，青い円に沿った回転角と同じだけ逆向きに回転するので，初めに直線OK上にあったC点は回転しても直線OK上にあります．

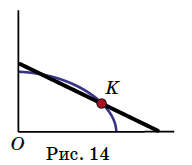
■楕円軌跡
もしクバンチク君がいる場所が，梯子の中心ではなく，例えば，1/3の位置にいるなら，クバンチク君の描く軌跡はどうでしょうか？

■ここで，興味ある問題を補足します．
円が2倍サイズの円の内部に接しながら，滑らないように回転するとします．内部の円の中心が一周した（公転）とき，内部の円は何回転（自転）したでしょうか？

答えは1回転です．お試しください．外側の円の円周は内部の円の円周の2倍ですので，2回転と言いたいところですが，不思議ですね．何故だか説明してください．

同じ大きさの円を接して回したとき，外側の円は何回転するかという良く知られた問題があります．10円玉を２つ使って実験してください．この場合は，円周の長さは同じですから，1回転と言いたいところですが，このときの答えは2回転です．