魔法陣の応用

KVANTIKの2019年12月号に，下記の数学ツアー問題の解説がありました．
出題されている問題は：
9個の金のインゴットがあり，それぞれに
100g，200g，300g，400g，500g，600g，700g，800g，900g　の刻印があります．しかし，1つのインゴットの重量だけが宣言された刻印よりも小さいことがわかっています．分銅なしの2皿天びんを使ってこのインゴットを見つける方法は？

皆さん挑戦してください．かなり難しい問題です．
さて，この問題は3x3の魔法陣と関係があることが指摘されます．

１～９の数字を3x3のマスに配置して，縦横斜めの3つの数の和がいつも15になるように配置したものが魔法陣です．1+2+3+･････+9=45ですが，中心の数Xは，4重に数えられます．従って，45+3X＝15x4　を解いて，X=5が決まります．3x3魔法陣の中心の数は5でなければなりません．
周囲の数を埋めて行き，3x3魔法陣が作れますが，3x3の場合は魔法陣の解はこれ一つ（対称的な入れ替えは同じとする）であることが知られています．

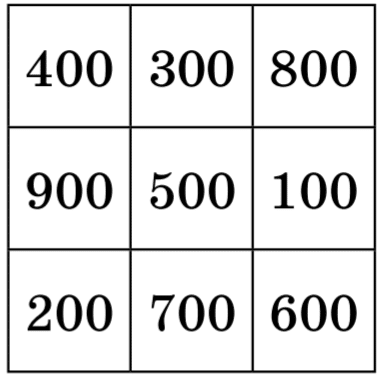
金のインゴットの問題に戻ると，上図の魔法陣になります．縦横斜めの和はいつも1,500になります．魔法陣の縦横斜めの3個のインゴットで1組作れば8組できます．8組から2組選び天秤に載せ比較し，軽い方の組みにしるしをつけます．例えば，以下の赤で囲んだ組が軽ければ，交点にある900gが軽いインゴットであることがわかります．横2回，縦2回の4回測れば必ず見つけられますね．

■補足：
和が一定になるのではなく，積が一定になる魔法陣はどうやって作れるでしょうか？以下の例をご覧ください．