3角空間の世界

Пространство треугольников • Библиотека

«Квантик» No1, 2021に，アレクセイ・パノフ，ドミトリ・アル・パノフ，ピョートル・パノフらによる表題のエッセイがあります．この問題を発展させると，私の興味に関わりのある分野へつながりそうなので，まず，基本的事項を簡潔にまとめておくことにします：

■正3角形の内部の1点から，それぞれの辺に下した垂線の和は，常に一定であることを証明しなさい．［各自試みてください］

つまり，△ABCは正3角形で，内部の任意の点Tから，各辺に下した垂線の長さの和　a+b+c＝正3角形の高さ（一定）　ということを証明してください．

■長さa,b,cの３つの線分が，３角形を構成できる条件は，
どの１辺についても，残りの２辺の和の方が大きくなることです．
もし，そうでなければ，３つの線分が繋がることができません（あるいは，三角形がペチャンコになります）．

つまり，以下の3つの３角不等式が同時に成立することです．
a < b + c
b < c + a
c < a + b

この３つの3角不等式が同時に成立する点が存在できる領域は，
下図に示したような４つの合同な正3角形の真ん中の小さな正3角形の内部であることは明らかでしょう．この真ん中の小さい正3角形の内部を”3角空間の世界”と，このエッセイでは呼んでいます．

■”3角空間の世界”の地図作り
簡単のために，△ABCの高さを１とします．従って，a+b+c=1です．
”3角空間の世界”の内部の点を，a,b,cで表すことにします．

以下の図では，このような点を3点ほど表示しています．

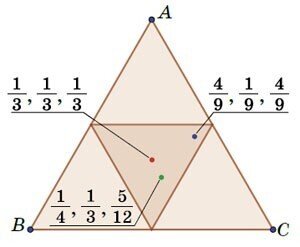
次に，a,b,cの数字を入れ替えることを，このエッセイでは順列と呼んでいますが，私は対称性と呼んだ方が適していると思います．対称性を考慮して，”3角空間の世界”の点を色で分類した図が以下です．

赤い点（中央）：a=b=c　で作れる3角形は正3角形
緑の点：a≠b≠c≠a　で作れるのは一般の3角形
青い点：a＝b or b=c or c=a で作れるのは2等辺3角形

［訳者注）ここで，現れる点の数は，結晶点群でいう，特殊点と多重度の関係と同じです．つまり，緑の点は一般点で，多重度は１，同価点の数は6個．青い点の多重度は２，同価点数は3個．赤い点の多重度は６，同価点数は１個です．］

■次に，a,b,cの数値を（R,G,B）の色と考えることにします．
点は△ABCの内部にあるとし，0≦a,b,c≦１です．
(1,0,0)は赤，(0,1,0は緑，(0,0,1)は青です．(0,0,0)は黒，(1/3,1/3,1/3)はグレー，(1,1,1)は白などです．△ABCの点を，このような色（a,b,c）に基づき着色することが自然なのですが，このようなカラーリングは，残念ながらコントラストが低く，明るさも足りません．そこで，(1-2a, 1-2b, 1-2c)と計算した色で着色するとうまく行きます．［訳者注）この変換の意味は，△ABCの点を，"３角空間の世界"△RGBの中に反転して写像するようなものです］

■さらに2つの地図
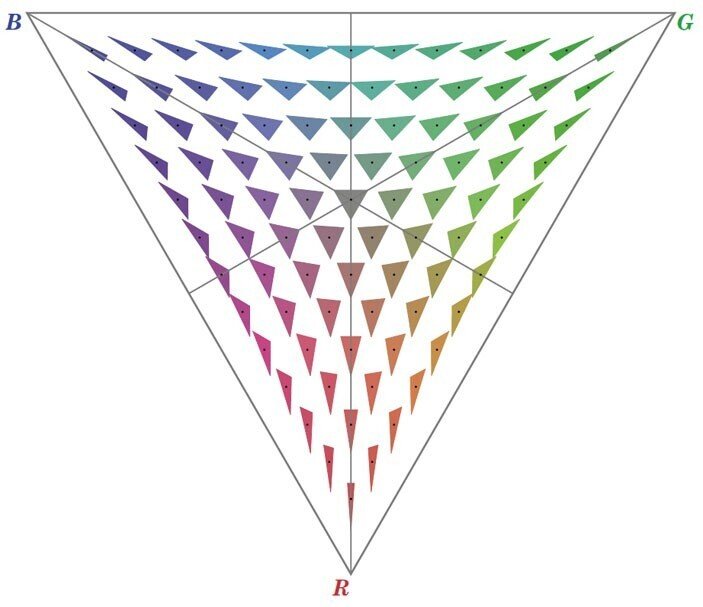
さまざまな種類の地図は，私たちを取り巻く世界の理解を広げてくれます．”３角空間の世界”を均等に埋める点のネットワークを示す別の地図が以下の図です．

次の地図では，色のついたドットが，そこの形に対応する小さな3角形アイコンに置き換えられています．