
エンペドクレスの4つの要素・続き
実験4「グラスはなぜ歌うのか」では、ガラスの縁に沿って濡れた指を動かすとガラスが鳴るようになりました。ガラスは川の砂でできており、他の岩石(花崗岩、大理石、石灰岩など)とともに地球の地殻の一部であることが知られています。このように、ほとんどすべての固体体は、エンペドクレスの「土」の要素と考えることができ、そのすべてが音源となりうる。では、なぜ固体の接触が音の発生につながるのか、その疑問に答えてみましょう。
実験4 "グラスはなぜ歌うのか?"
グラスがなぜ歌うのかを理解するためには、まず音とは何かを理解する必要があります。これは別の記事で取り上げますが、今のところは「音は空気の振動である」と言っておけば十分です。
固体の振動を伝達して、空気が振動することがよくあります。例えば、人が話すと声帯が喉の中で振動して声が出る。人がギターを弾くとき、弦を揺らしたり、捻ったり、指で叩いたりして音を出します。少し違うのは、バイオリンを弾いた時の音です。ミュージシャンが弓で弦をこすると、摩擦で弦が引っ張られている状態になりますが、弾性力はそれを引き戻す傾向があり、この力が摩擦力を超えるとすぐに、弦は戻り繰り返され、音が聞えます。
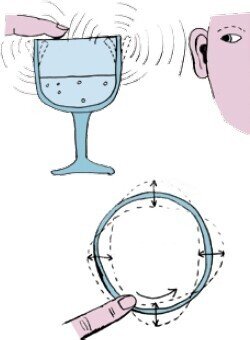
歌うグラスは、バイオリンとほとんど同じです:グラスの縁に沿って指を走らせると、皮膚の小さな凹凸がグラスにまとわりついて、グラスが振動します。バイオリンの弦との違いは、これらの振動がミクロなもので、目で見ることができないことです(指で感じることはできますが)。しかし、グラスの中に水がある場合は、グラスの水面に波が現れるのを見ることができます。これは、ガラスが本当に振動していることを意味します。
実験を成功させるためには、ガラスと指が油っぽくないことが重要です(摩擦力がここで働くので)。
水の入ったグラスの方が水の入っていないグラスよりも低い音がするのはなぜでしょうか?正確な説明は簡単ではありませんが、おおよその現象は次のように説明できます。
空気の振動をゆっくりとさせるような音が、私たちには低く見える。
ここで、バネ振り子で、バネに重りをつけたものを想像してみましょう。Kvantikのサイトに投稿された動画では、プラスチック製のバネとミカンで作れるバネ振り子の振動を確認することができます。経験上、ミカンのあるバネは、ない場合に比べて、はるかに振動数が小さいことがわかります。実際、荷重が大きくなるほど、バネが元の位置に戻るまでに時間がかかります。グラスに水を入れると質量が増えるので、ミカンをくっつけたときのバネのように振動数が小さくなります。
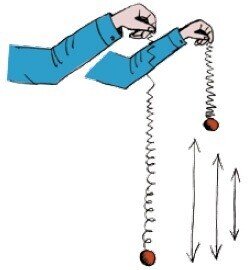
http://kvantik.com/files/materials_2014_07.html
2つのフォークを取り、それらを組み合わせ、それらの間の隙間に木製のつまようじを刺します。次に、この構造をガラスのゴブレット(または背の高いグラス)に置き、つまみでガラスの端にのみ触れるようにします(右の写真を参照)。同時に、構造物が落ちないように、端にしっかりとぶら下がるようにしてください。これが実際に実行できるという事実は、Kvantik Webサイトのビデオに示されています。
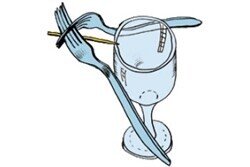
次に、2つの質問に答えましょう。
1. 2つのフォークと1つのつま先の構造が非常に安定しているのはなぜですか?
2. この構造の重心はどこにありますか?
古代ギリシャの有名な科学者アルキメデス(紀元前287~212年頃)は、彼の2世紀前に世界の根源を4つの要素としたエンペドクレスがいたアクラガス(現在のアグリジェント)の町から100キロ離れたシラクーサ(シチリア島)に住んでいました。アルキメデスは幾何学が好きだったので、いくつかの物理法則を発見し、そのうちの1つには彼の名前が付けられています。

アルキメデスの法則は次のように述べています:液体(または気体)の中に沈められた身体は、身体によって変位された液体(または気体)の重量に等しい力を受けます。紀元前1世紀に生き、ユリウス・シーザーの時代にローマの水道橋を設計したローマの建築家ヴィトルヴィウスの書物から、世界は初めてアルキメデスの法則を知った。ヴィトルヴィウスによると、アルキメデスは入浴中に自分の法則を発見し、その直後に裸で家から飛び出し、ギリシャ語で「見つけた!」という意味の「ユリイカ!」と叫び始めたという。

アルキメデスが発見した同じように有名な法則に「てこの法則」があります。古代ギリシアの作家プルターク(45-127)は、アルキメデスが「てこの法則」を利用しようとした珍しい方法を伝えます。アルキメデスは、友人でもあり身内でもあるギエロン王に、与えられた力でどんな重さでも動かすことができると書いたことがあります。要するに「支点をくれたら世界をひっくり返す」ということです。

アルキメデスは、物体の重心の概念を最初に導入し、三角形や平行四辺形の形をした平たい物体の重心の位置を求めた。忘れてしまった方のために、物体の重心とは、その物体の重力の力(地球に引き寄せられる力)が集まる点です。覚えておきましょう。
壁に打たれた釘に物体を吊るすと、数回の振動の後、物体は静止し、その重心は懸垂点の下、つまり懸垂点から垂直に下っていく線上にある。この重心の性質を利用して、図に示した図形の重心の位置を求めてみましょう(Kvantikのサイトの動画も参照してください)。まず、A点から物体を吊り下げ、落ち着いたらA点を通って赤い線を縦に引きます(右図のように)。次に、同じようにB点から物体を吊り下げて青い線を引きます(右図のように)。この図の重心であるC点で線が交差していることがわかります。多くの場合、物体の重心がこの物体の外にあることもあります。Kvantikのサイトに掲載されている動画を見ると、2つのフォークを繋いだ時の重心が2つのフォークの間にあることがわかります。
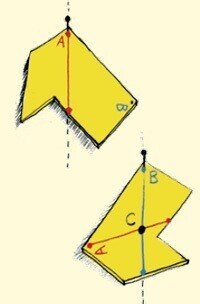
実験5 なぜフォークは落ちないのか?
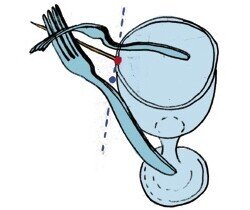
2本のフォークをつまようじで固定した構造が、ガラスの端に置いたときに非常に安定していることを示しています。安定している理由は、構造物の重心が支点の下にあるからです(左の図で重心が青、支点が赤で表示されています)。この説明が本当なのかどうかは、もう一回実験してみると(Kvantikのサイトの動画を見てください)わかると思います。
実験6 ボールはどうしてグラスの中に入るのか?
卓球のボールとグラスを持って、テーブルの上にあるように置きます。手などでボールを触らずにグラスに入れることは可能でしょうか?ボールをテーブルの端に押し付けて、グラスでキャッチするなどは禁止です。実際にこれが可能であることは、Kvantikのウェブサイトに掲載されている動画でも紹介されています。
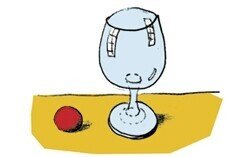
では、2つの質問に答えてください。
1. グラスの中にボールを引きあげ保持する力は何か?
2. この実験は、グラスの壁が上に伸びている形状でも可能でしょうか?
実験6 ボールはどうやってグラスの中に入ったか?
グラス逆さにしてボールにかぶせ、グラスを回転させる。ボールがグラスの中で回転するようにグラスの壁をボールに押し付け続けます。グラスの口(首)の近くでは壁が先細りになっていて、その傾斜のために横だけでなく上にもボールを押し上げます。ボールの立場で見た場合、それは、遠心分離機や回転木馬のように、ガラスの壁に強く押し付けられ、グラスの軸から最も遠い領域(グラスの壁)に押し出されます。(動画を見るとよくわかります)https://old.kvantik.com/files/materials_2014_08.html
口(首)が拡大しているグラスの場合、この方法は適していません:ボールはグラスから排除されます。
アーティスト アルチョム・コシュチュケヴィッチ
参照
コンスタンチン・ボグダノフ氏による大衆科学講演会「私たちの中の物理学」,2007年12月13日,モスクワ,ФИАН
