1次元並進があるロッドの対称性レビュー
ロッドの対称性のタイプを導く方法は,点群(特異点1点を含む図形の対称性)の変換と1次元空間群の変換とを組合わせます.
並進を集めると並進群(a)を作ります:軸に沿ってのらせん運動や映進面にも付随した並進成分があります.
並進群の変換と点群の変換を組み合わせてできる空間群は,シンモルフィック(=共形)と呼ばれます.例えば以下のもの:
(a) ・n ; (a)・~2n; (a)・n:m; (a):2:m ; (a)・n・m;
(a):2・m; (a)・n:2; (a)・~2n・m; (a)・m・n:m
シンモルフィック群は,並進が作用するもとの図形の点群を部分群として含んでおり,もとの有限図形の形状が空間群にそのまま残っていることから「共形」という術語ができました.このようなロッドの無限並進の形状は,元の形状の周期的な繰り返しになっています.
非シンモルフィック空間群を得るためには,シンモルフィック点群(すなわち,対応するシンモルフィック空間群を生成するのに用いた点群)の記号で,生成対称元を,並進成分を含む対応する組み合わされた対称元に置き換えます.
例えば,
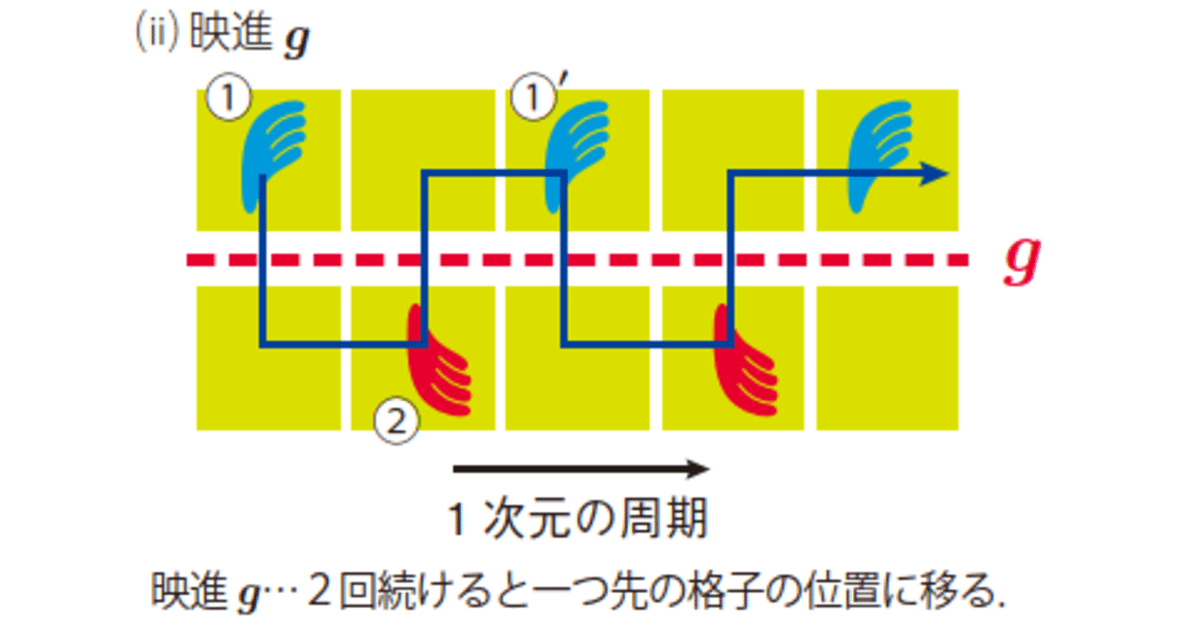
対称軸nはらせん軸n_jに,対称面mは映進面~aに置き換える.どちらの演算も,回転しながら並進したり,鏡映しながら並進したりして,並進の成分が隠れています.
このような置き換えは,すべての生成元に対して行われ,ただし,
演算操作を繰り返したとき,群(a)の並進と合わなくなる組み合わせは許されません.このプロセスの結果得た図形は,もはやシンモルフィック群の対称性を持たず,その可能な部分群の1つの対称性を持ちます.
3回軸,4回軸,6回軸のみが許容される結晶学的な対称群を,1次元のロッドに対してリストアップしてきました.まだ途中ですが,今日は全体の考え方を述べておきたいと思います.
非シンモルフィック空間群をシンモルフィック群の部分群と見なすこともできますが,シンモルフィック点群の演算と,いわゆるモジュラスによる群の演算の間の同型関係により,シンモルフィック群の変換の積は,相当する非シンモルフィック群の変換の積に対応されられます.
モジュラスによる群とは詳しい説明が必要ですが,係数を法として合同という考え方のことです.例えば,連続に続く時間を,時計の文字盤の1~12の数に閉じ込める[時計を1回りすると同じ数字になる=12を法として合同という]のと同じです.無限に並ぶ1次元の格子点のどれもが同じと見なせるので,らせん軸や映進面で,一回りした時1つ先の格子点に移動していても動いていない(元に戻った)と解釈することです.この考え方は空間群の理論で非常に重要です.
映進面~aの操作を2回続けて行う(映進面の位数は2),らせん軸n_jの操作をp回続ける(n_jの位数がpのとき)と1回転し,格子は1つだけ並進します.[~a^2≡1(mod a), n^p_j≡1(mod a)]
モジュラスにより合同とは,並進aの周期分の並進はゼロと見なすということです.シンモルフィックと非シンモルフィック点群(後者には,単純な点群の操作だけでなく,並進成分が組み込まれた「らせん」や「映進」の操作が含まれる)は互いに同型でその位数は等しい.
