
PenroseタイリングとAmmann線の関係
■ PenroseタイリングとAmmann線
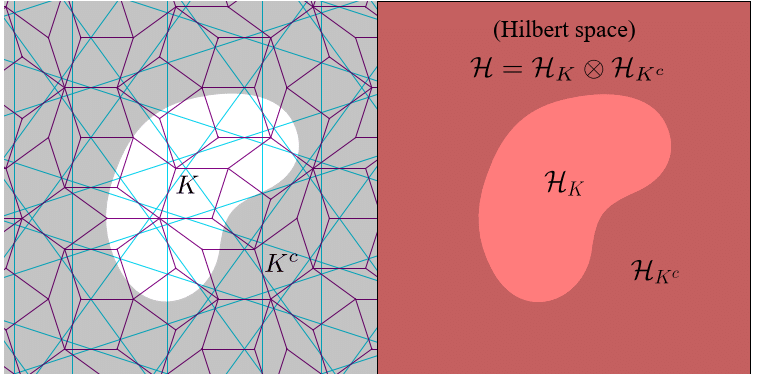
Penroseタイリング(小豆色の線)は,太った菱形と痩せた菱形の2種類のタイルで出来ている.Ammann線とは,タイルの表面に描かれた線分(装飾)のことで,これらの線分が繋がり5つの方向に走る直線[青色直線=Ammannバーと呼ばれる]になるようにタイルを組み合わせると,非周期のPenroseタイリングが完成する.アマチュア数学者Robert Ammannが,Penroseタイリングを観察していて発見したものだが,その一般的説明や構成原理はまだ十分に解明されていない.

下図に示すようなタイルの表面に描かれたAmmann線分は,Penroseタイルの縁に矢尻マークで与えたPenroseのマッチング規則と局所的[有限領域で]に同値である.
Penroseタイリングは多くの興味深い性質を持っており,いくつかの方法[置き換え法(分割とインフレーション),カット&プロジェクション法(高次元空間の切断と射影)]で生成することができるが,Ammann線は,Penroseタイリングを高次元周期空間と結びつける鍵になるので興味深い.部分周期が観測されるのも,高次元空間を2次元に投影したためであろう.
イスラムのモザイク模様を見ていると,大きなタイルユニットを張り詰めて作られているが,大きなタイルユニットのなかに,あたかもAmmann線を思わせるモザイク模様が描かれいるのに気づく.
イスラムのモザイク模様の特徴は,フラクタル性,自己相似性(自分の中に縮小された自分か繰り込まれていく)で,高次元瞑想空間へと誘われる気持ちになる.(giriタイルと呼ばれる5種類のタイルで作られるモザイク模様にはAmmann線を思わせる線分が見られる)


タイル内部に描かれた黒い線分がAmmann線.
(b) Penroseタイリングのインフレーションルール.親菱形がインフレーションを起こすと,いくつかの子菱形の半分が生成される.この子菱形の半分は,隣接する親菱形のインフレーションによって生じる子菱形の半分(薄い色で示す)と組み合わされると親菱形と同じ菱形になる.
[図は *1)より借用]
■ カット&プロジェクション法
カット&プロジェクション法は,1981年にドイツのEindhovenのN.G.de Bruijnによって代数的に研究された.彼の学生だったBeenkerは,これに基づきタイリングの全ファミリーを提示した.これには,Ammannがすでに独自に発見していたAmmann-Beenkerタイリングも含まれる.
Penroseが局所5回対称の非周期タイリングの発見は1974年,Martin Gardnerにより広く知られるようになったのは1977年だった.
Ammannの局所8回対称の非周期タイリングの発見は,Penroseの局所5回対称の非周期タイリングの発見と,ほとんど同時期であったが,Ammannはアマチュア数学者であったため知られるのが遅れた*2).
カット&プロジェクション法は,$${n}$$ 次元ユークリッド空間 ($${n>2}$$) を 2 次元平面によりデジタル化したとみなすことができる.最も簡単な$${2→1}$$ でタイリングの概念的な説明をしよう.
■ 高次元空間からの影(2次元の周期的世界→1次元の非周期の世界)

1辺の長さが1の正方形のタイル(赤色格子)を隙間なく張り詰めた周期的な2次元世界があります.タイルの中心に格子点があるとして,格子点を“1次元世界(水平な青色の線)”に射影しましょう.この1次元世界(青色の水平線)が過るタイルだけが影を作る対象になります.
①2次元の世界は,1次元の世界1,2,3,4,5,6……(それぞれ色を変えた)を束ねてできています.射影のスクリーンとなる1次元世界(水平な青色直線)は,これらの1次元世界1,2,3,4,5,6,…と角度 α で交
わっています.tan α =n/m と有理数なら,1つの格子点が青色の直線に乗れば,その格子点がある部分空間の中で m 個のタイルを動き,他の部分空間に向って n 個のタイルを動いた場所にある格子点は,また青色の直線に乗っているはずで,青色の1次元世界にも周期ができています.もし tan α が無理数なら,1つの格子点が水平な青色直線に載ったら,他の格子点でこの直線に載るものはないはずです.このときは,青色の1次元世界は非周期になります.
②射影されてできた1次元の非周期格子を,図の下に取り出しました.
この非周期格子の格子点は,各1次元空間1,2,3,4,5,6,…内に起源をもつ間隔と,次の1次元世界に飛び移るときに生じる間隔との2種類の間隔が混ざってできています.
③この非周期格子は,周期的2次元空間から1次元空間への射影で作りました.周期的2次元空間の1次元の断面そのものではありません.
■ $${n → 2}$$
周期的な$${n}$$次元空間の格子点を,その部分空間である2次元の平面に射影してタイリングを作る.この2次元平面(傾斜平面)には1つの格子点が原点として含まれるが,他の如何なる格子点も含まれない(有理数勾配の線は含まれない)場合は,タイリングは非周期である.
Penroseタイルの場合がそうであり,これを定義するタイル集合は非周期:これを用いると非周期タイリングしかできない.
$${5→2}$$の場合は,Penroseタイリング(5回対称準結晶);$${4→2}$$の場合は,Ammann-Beenkerタイリング(8回対称準結晶)が作れる.
概念的な説明でまとめると次のようになる:
Penroseタイリングを例とする:5次元の周期的な空間の内部に,非有理数勾配の斜面「2次元の部分空間」を想定し,5次元周期空間をこの2次元に射影すると非周期の2次元パターンが得られる.この2次元パターンには,射影面の補空間の情報が畳まれて反映されているのだが,これが部分周期やAmmannバーの形で現れてくる.
引用文献
1.The Penrose Tiling is a Quantum Error-Correcting Code; Zhi Li and Latham Boyle; arXiv:2311.13040v2 [quant-ph] 25 Jan 2024
2.Images of the Ammann-Beenker Tilling; Edmund Harriss;
https://archive.bridgesmathart.org/2007/bridges2007-377.pdf
3.Ammann Bars for Octagonal Tilings;Carole Porrier Thomas Fernique;arXiv:2205.13973v2 [cs.DM] 7 Nov 2022
4.美しい幾何学,谷克彦,技術評論社(2019)
