
クバンチクより翻訳(合同な3角形への分割)
合同な3角形への分割
3角形をどのように分割したら自分に合同な小さな3角形になるか?
このような分割でいくつの3角形ができるか?
正3角形を小さな正3角形に分割すると:4個から無限大
正3角形を4つの正3角形に分割するのはとても簡単です,各辺の中点を線で結ぶ(図1a)

同じように分割を続けると,合同な正3角形がどんどんできます.7,10,13,... 3k+1個(kは自然数)[訳注)3角形を1つ潰して小さな3角形が4つ生まれます.大小ありますが合同な正3角形はこのように3個づつ増えていきます]
分割で生まれた3角形は,必ず合同になることに注目してください.同様にして,自己相似の図形の1つシェルピンスキーの3角形が作れます(そのような図形はフラクタルと呼ばれます)

正3角形で中線を描き,生じた4つの三角形の真ん中を取り除く.このプロセスを残りの3つの三角形でもそれぞれ繰り返し,これを無限に続けます.
(図 1, b)
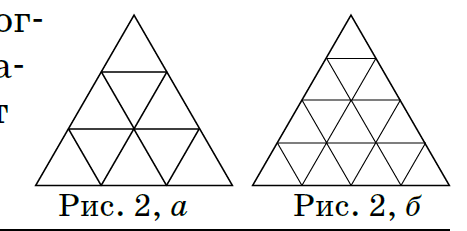
もし,正三角形の辺の分割を2等分ではなく,3,4,...分割ではどうでしょう?そのときは,9,16,...個の正角形に分割できます.(図2,a,b)
結局,1辺をn個に等分割すると,小さな三角形の辺は元の辺の1/nになり、面積は1/n^2になります.これは,n^2個の3角形ができることを意味します.
それらの数は「層」の積み重ねで数えられます:
最上層--1個の三角形,2番目の層--3,3番目の層--5,...,n番目の層--2n-1個の三角形があります.
1 + 3 + ... +(2n-1)= n^2であることが幾何学的に証明されました.
任意の3角形に一般化
各辺に平行な線で分割する.

図3.aは6個の相似な3角形,図3.bは8個の相似な3角形,図3.cは11個の相似な3角形.
しかしながら,2個,3個,5個の相似な3角形で分割はできません.
直角3角形では
△ACBをCDで相似な2つの3角形に分割できるならば,△ACBは∠ACBが直角な直角3角形であることが示されます.

図5は74=5^2+7^2個の合同な直角3角形からなる.

異なる相似比の3角形への分割
もし,k+k^3=k^4が成り立つなら,△4と△5は合同になる.△7と△8も合同になる.k^6=k^2(k+k^3)=k^3+k^5<k+k^3+k^5

結論に代えて
どんな3角形が5つの相似な部分に分割できるかわかっていない.
Б. Френкинの論文«О разрезании треугольника на подобные ему»
(«Квант»№ 4 2008 г.)
多角形に対してこのような分割をするのは
М. Гарднера «Математические досуги» (Мир, 2000; гл. 24:
«Делящиеся» фигуры на плоскости).
この記事が気に入ったらサポートをしてみませんか?
