繰り返し模様p3m1とp31m

■第14のクラスは，国際記号でp3m1，ロシア式記号で(a/a):m･3と記述します．対称性3･mの図形を60°で交差する等価な２つの軸(a/a)に沿って並進させて得られますが，鏡映面（赤色）の入り方が，並進軸（青色）に直交している．

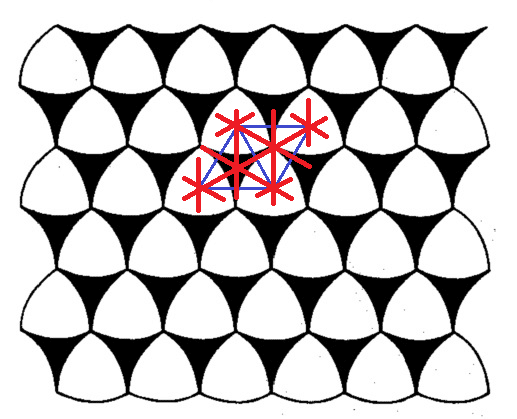
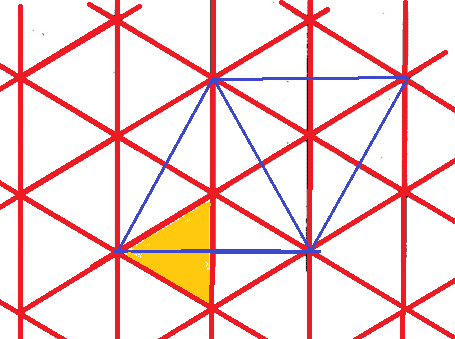
非対称要素（黄色）が6個で単位胞を埋める．

■第15のクラスは，国際記号でp31m，ロシア式記号で(a/a)･m･3と記述します．並進の格子は(a/a)で同じですが，鏡映面の入り方が，並進軸方向に平行である．(注意)多くの書物で，p3m1とp31mを取り違えているのを見かける.

上の図で鏡映面は格子に重なっている．非対称要素（黄色）が６つで単位胞を埋めている．

■この両者の区別は多くの書物で混乱がみられます．分かりにくいので，もう少し詳しく説明を加えましょう：

美しい幾何学，p.100，p.110より引用

美しい幾何学