
正方形の1辺の1/nを折る
Rachel Thomas, https://plus.maths.org/content/folding-numbers?nl=0
正方形の紙を1/2に折るのは簡単です.しかし,1/3に折るのはどうですか.
少し試行錯誤すればできるかもしれませんが,試行錯誤せずに1/3に折れますか?1/5は?1/7は?
■1/3に折る
はじめに,正方形の紙の上部の半分に小さな折り目マークを付けます.
次に,左下の角を,この中間のマークに合わせて用紙に折り目を付けます.


最初に気づくのは,作成した3つの三角形の興味深い関係です.1つは左上に,もう1つは右上に,もう1つは右下の用紙外に飛び出した用紙の裏面の小さな三角形です.これら3つの三角形は相似な直角3角形で(三平方の定理が成立)あることです.
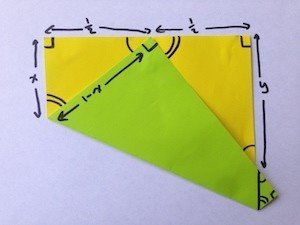
ピタゴラスの定理から
x^2+(1/2)^2=(1-x)^2 を解くと,x=3/8
相似だから
x/(1/2)=(1/2)/y なので,y=1/4x=2/3
かくして,y/2=1/3が得られる.

■これを一般化し,上端の辺上の比率をk:1-kとすると,
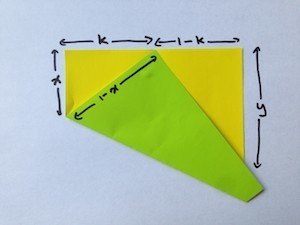
x^2+k^2=(1-x)^2 より X=(1-k^2)/2
y/(1-k)=k/x より y=2(1-k)k/(1-k^2)
すなわち, y/2=k/(1+k) の関係が得られます(これをHAGAの定理というそうです)
この関係式に,kの値(位置)として,得られたy/2の値(位置)を
代入するたびに,次のy/2の値(位置)が求まります.
k=1/2 → y/2=1/3
k=1/3 → y/2=1/4
k=1/4 → y/2=1/5
......
このようにして繰り返せば,一辺の長さの1/nまで順番に作れます.
つまり,正方形の上の辺にkの位置をとると,右側の辺にy/2に位置が決まります.このように続けると,1/2,1/3,1/4,・・・の位置が正方形の周りを
ぐるぐる周りながら順次現れるのが大変面白いです.





■さて余談ですが,紙の形が長方形の場合は如何でしょうか?
手紙を3つ折りにして封筒に入れるときにこのようなことが必要になります.長方形の辺の1/3を作る方法は,メルマガ[2015.04.07]で言及しましたがTAKAKUBO氏からの以下の2通りの情報が寄せられました.以下の図をご覧ください.
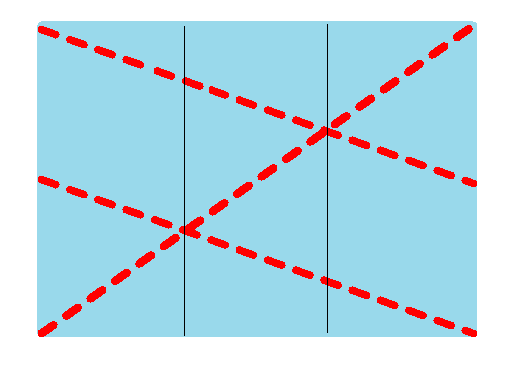
紙を筒状に3重に巻いて,2つに折れば6等分されます.
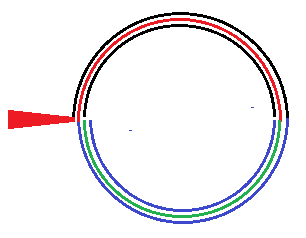
これらは一般の長方形(辺の比が1:√2に限らない)で使えます.
