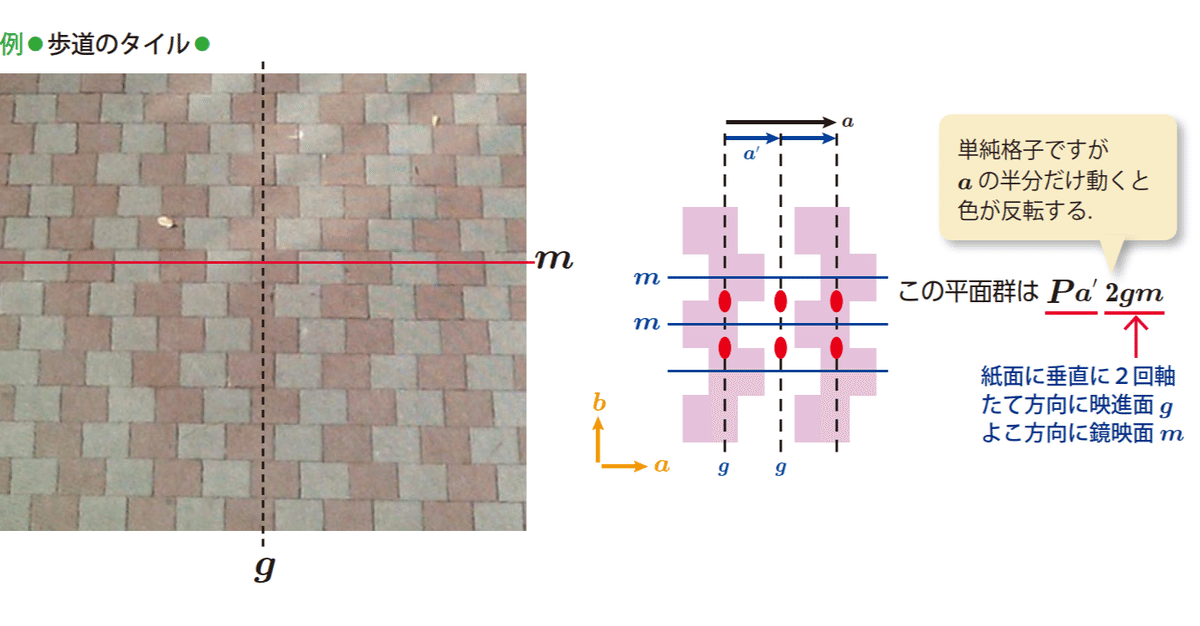
壁紙模様の対称性とその心理効果

人間は様々な用途で無限に繰り返す平面パターンを使います：壁紙，寄せ木細工，タイルの床，瓦屋根，陶器や装飾石の壁，レンガや敷石，道路や広場の舗装，色織物，カーペットや編物，同一物の密な充填，金属やプラスチック板から標準物を大量に打ち抜く，その他の多くの分野で利用されます．

自然界の網目パターンは，魚の鱗，生体組織の細胞，ハチの巣，マツカサの鱗片，などの配列で見られます．特に興味深いのは，結晶中の，原子・イオン・分子が配列した網平面です．もちろん，これらを直接見ることはできませんが，X線や電子線の回折や，走査型顕微鏡を用いて観測できます．
網目パターンから受ける印象を分析すると，芸術家が特定の視覚効果を伝えるために，特定の対称性クラスを意識的に選択する法則を確立できるかも知れません．

例えば，斜交する並進軸を持ち，対称面を持たないパターン（図112）は，斜め方向の動きを強調したい場合に適しています．

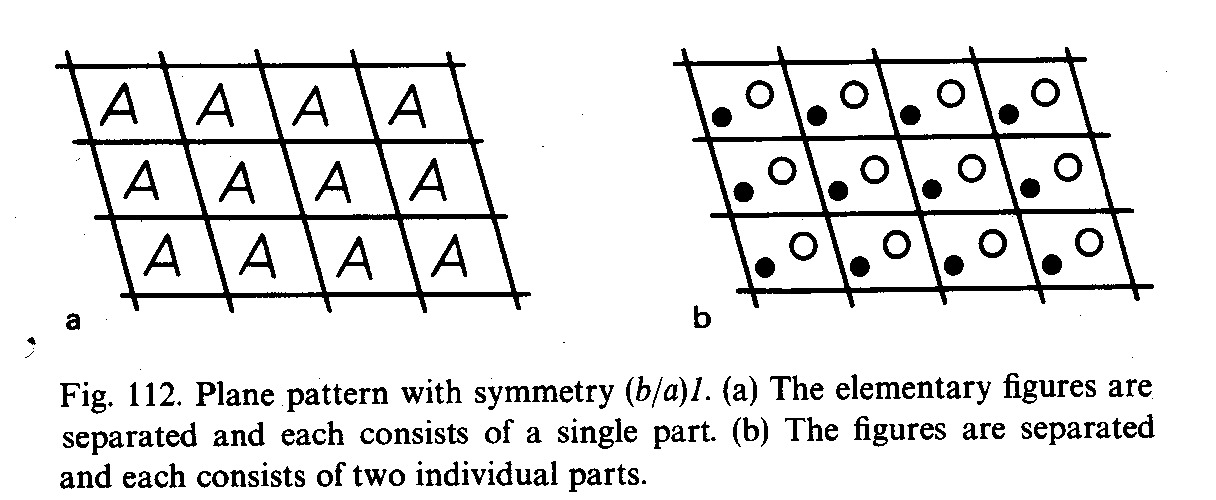
階段，ロビー，エスカレーター，地下鉄の傾斜トンネル，アーチ橋のフェンスなどの壁を飾る際に，芸術家はこの問題に遭遇します．

図117

図121

図123

水方向の並進軸はあるが，垂直方向の対称面を持たないパターン（図115，117参照）は，特定方向として水平面に沿った動きを強調しているので，地下鉄や回廊の水平通路の装飾に用いると成功します．対称面があると，それらに垂直な方向への運動を止めます．例えば，図121,123などのパターンは，水平方向には静止しているように見えます．図121では，２回軸が存在することで，上下方向への運動の概念が生まれますが，図123では，それらの回転軸が存在しないので，上方向，あるいは一般的に，垂直な一方向の運動の印象を与えています．
図121は，回廊の水平な床や天井の装飾にふさわしく，図123は， 地下鉄の昇降路の床や天井の装飾に適しています．

図128

図130

図137

図147

水平や垂直の対称面のシステム（図128,130,137,147）がいくつか存在することで，静止休息，記念碑性，不動性，重力などの印象を醸し出します．興味深いことですが，(b:a):2･m型の対称パターン（図128 と 130）は，長い間，壁紙に使用されてきました．そして，図137や147に示すようなさらに対称的なパターンは，寄せ木，天井，ステンドグラス窓などには使われました．
奇妙な静止のない印象は，主要部分に映進面がある対称パターン（図116と120）で生み出されます．言葉でうまく表現できないのですが，これらのパターンの中の図形が，押し合い，転がり，絡み合い，群がって動きがあります．

図116

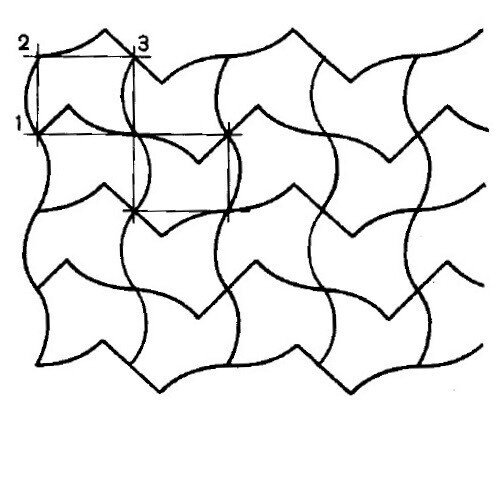
図120

このタイプの対称性は，他の対称性よりも出会う頻度は少ないのですが，それは，他のものよりも構成や認識が困難であるためで，例えば，見本市会場や遊歩道などのデザインに利用されることがあります．

図132

図139

図145

特に興味を惹くのは，対称面がなく，3,4,6回回転対称軸で特徴づけられるパターン（図132,139,145）です．このようなパターンは，そのダイナミックさから，ダンスホールなどの大勢の人が無秩序に動くことを想定した施設の床や天井に適しています．図116のようなパターンと合わせて，文化公園の広場やサーカスのテントのアリーナ，フローティング・パネルなどの装飾に使用されています．全体として静止休息の奇妙な印象と細部に見られる動きは，普通の対称面と映進面が交互に繰り返すパターンのせいで生じています（図12,135,142）．静止休息と運動の印象のどちらが支配的になるかは，フレーム・ワーク（垂直，水平線に）に対するパターンの方位に大きく依存します．

図135

図142

例えば，図12はこの本に掲載している向きでは，動きの印象が静止に打ち勝ってしまう．特別な注意を払わずにパターンを見ると，対称面を見落とすのです．
一方，図12と同じ対称性を持つ図135は，動きよりも静止の印象が打ち勝ってしまう．それは，本を普通に置いたときに，パターンの対称面は垂直・水平線に沿ったフレームに平行で平行であるからです．
観客が網目パターンを見たとき生じる印象に対称性が演じる役割について詳しく述べてきました．明らかに，対称性が美的鑑賞の唯一の要因ではありませんが，パターン構築の基礎となる法則を明らかにすると，装飾美術で対称性の果たす役割は，デッサンで遠近法が果たす役割と同じです．

■最後に，私が気に入っている映進面のある軽快な歩道タイル張りの写真を掲載します．美しい幾何学p.93より

美しい幾何学