
フェドロフの平行多面体と非対称要素立体★
Параллелоэдры(Parallelohedra)и стероэдры(Stereohedra) Федорова
フェドロフの平行多面体と非対称要素立体
一つの平行多辺形で,平面を隙間なく埋めるという問題は,3次元空間に対しても提起できます.空間では,平行多辺形の役割は,平行多面体が担っています.代表的な平行多面体には,立方体,2つの底面を持つ6角柱,菱形12面体,細長い菱形12面体,立方8面体(切頂8面体)の5種類があります(文末の図).隣接する平行多面体の面が完全に一致するように,同一の平行多面体で空間充填できます.すべての平行多面体は互いに平行に並び,重なりや隙間のない空間充填ができます.5つの典型的な平行多面体から,それを伸ばしたりずらしたりすることで,無限の派生平行多面体を得ることができます.
立方体から変形させると,直方,および,斜方の平行多面体,6角柱から変形させると,斜方の6角柱などになります.平行多面体の持つ対称性を考慮し同価な部分に分割(一般的には,これらの部分は非平行に配向)できます.分割された部分を非対称要素立体Stereohedronと呼びます.空間における非対称要素立体Stereohedronは,平面におけるプラニゴンPlanigonに相当し,離散体の最小分割単位です.それは,さらに小さい等価部分に分割することはできませんが,それらの部分は直交変換によって互いに変換し合います.ここでは,すべての非対称要素立体Stereohedronのカタログを作ることはせず,いくつかの例を挙げるにとどめます.
平行多面体が対称心を持たない斜方の平行六面体(対向面は異なる色に塗られている)である場合,その図形はもはや等分することはできず,それ自体がStereohedronです.平行六面体の中心に対称心がある場合は,その図形は2つのStereohedronに分割することができます.立方体は,対称面によって48個のStereohedronに分けられる(表紙の写真と下図参照).

E.S.Fedorovが離散体(結晶空間)の230種類の対称類を導出した際に,Stereohedronは大きな役割を果たしました.球などの最密充填の問題は,Stereohedronや平行多面体による空間充填の問題に還元できる部分もあります(B.N.Delaunay, 1934参照).
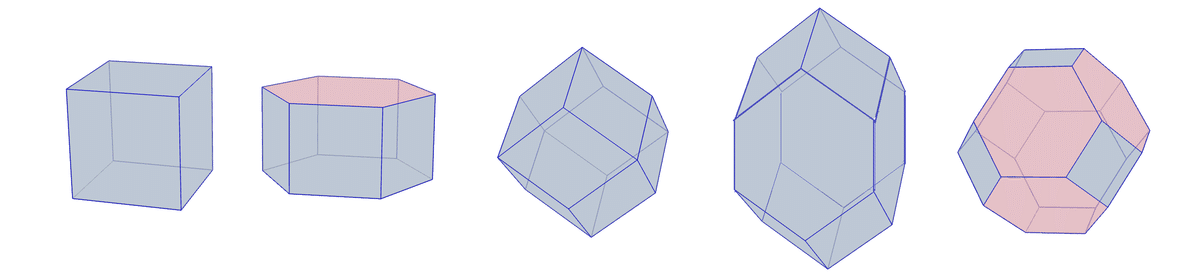
立方体,2つの底面を持つ6角柱,菱形12面体,細長い菱形12面体,立方8面体(切頂8面体)
次の項目へ続く
