クバンチクの問題より

お願い早く洗って．キャビネットの扉を反さなければならないのだ．

（問題）学校に1000個のワードローブ（キャビネット）があり，１，２，･･･，1000の番号が付いています．夜は，1000個すべてのキャビネットの扉が閉じられます．この学校には1000人の幽霊が住んでいて，真夜中に，最初の幽霊が，キャビネットのすべての扉を開けます．次に2番目の幽霊が，2で割り切れる数の扉の状態を変化させます（この場合は閉めることになる）．次に，3番目の幽霊が，３で割り切れる扉の状態を変化させます．同様に続けて行って，1000番目の幽霊は，1000で割れる番号の扉（この場合は1000番のみ）の状態を変化させます．その後，幽霊たちは消えます．いくつのキャビネットの扉が開いていますか．　（2016年2月のクバンチックの問題より）

■ヒント

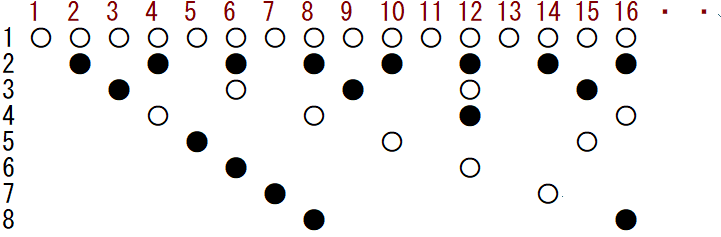
これは難問です．だいぶ考え込みましたが，面白い問題です．チャレンジしてみてください．ヒントに表を作ってみました．〇は扉が開いている状態．
整数ｎに約数aがあれば，適当な整数bがあって，n=a･bと書けるはずです．したがって，nの約数はペアで存在し，このペアの分は偶数個です．例外は，a＝bとなるときで約数a=bに関しては，奇数個（１個）存在します．nの約数の最後の１つは（n番目の幽霊が操作する）n自身です．扉nの約数はいつくあるか（奇数個か偶数個か）考えてください．