主軸n(垂直方向)と2回軸(横方向)の組み合わせ

ねじれた形状 ● 偏光面の回転

前回のタイプの対称性から，すべての対称面と対称心を取り除くと，残った対称軸は新しい対称のタイプn:2を作ります．このタイプの対称性は，前回のケースとは対照的で,すぐには認識しにくく，実際に意識して使用するためには，ある種の準備が必要です．この新しいタイプの対称性が，前回見たものよりも普及していないという事実はこのためでしょう．
前回の図形から対称面と対称心を取り除くには，図形を主軸の周りに小さな角度だけねじります．この操作は，図の他の部分が実際に主軸の周りで回転しているので，主軸はそのまま残ります．横方向の軸も，中央面（主軸に垂直な面）に位置しているので，そのままです．中央面は，ねじり操作の定義により，変形を受けません．小さな角度でねじられて，すべての対称面を失った4角柱プリズムを第2の図に示します．

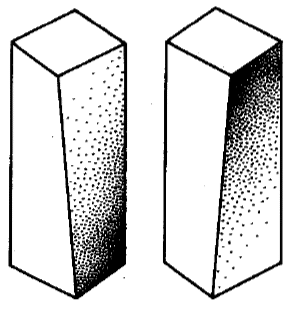
捻る方向（右か左か）によって，右巻きまたは左巻きのエナンチオモルフ図形が得られます．このような対称性は，結晶にはよく見られます．

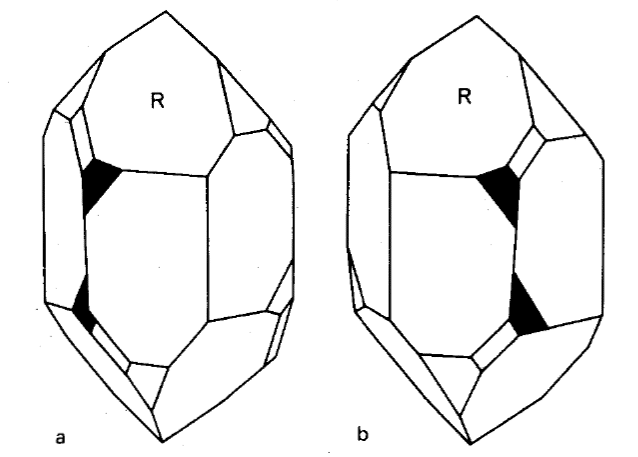
その典型的な例が石英です（図）．石英には，3回軸を主軸として，それに垂直な3つの2回軸があり，互いに60°の角度を成しています．主軸は垂直方向で2回軸（横方向）は，６角柱（６面体）の垂直な辺の中心を通っています．図で黒く塗られた台形面の配置から，この結晶には縦の対称面も横の対称面もないことがわかります．対称心と対称面の両方がないということは，右巻きと左巻きの水晶を区別できるというわけで，自然界には，どちらのエナンチオモルフも存在します．
水晶のR面（図）を観察者に向けて置くと，右巻きの水晶では台形の面がR面の右側にあり，左巻きの水晶ではR面の左側にあることになる．
私たちの表記法では，石英の対称性は3:2と記しますが，これは，この対称クラスが，1つの3回対称軸とそれに垂直な1つの2回対称軸によって完全に記述されることを示しています．
他の2つの2回回転対称軸は，3回回転対称軸の周りを120°回転させることによって，始めの2回回転対称軸から派生します．
水晶のエナンチオモルフは，水晶が右巻きと左巻きのねじれた形になることと密接な関係があります．また，内部の原子配列構造も関係しています．

（注意）実は，右水晶と左水晶の定義は，X線回折が発見され結晶構造の解析が可能になる以前に，結晶の外形から定義されたものです．結晶の内部構造がわかると，原子の配列にらせん構造があるのですが，左水晶は右巻きらせん構造で，右水晶は左巻きらせん構造であることがわかりましたが，名前の定義は変更せずにそのままですのでご注意ください．

一般に，これらの対称性のクラスを，n:2と表します．
このクラスは，1つの（主）n回軸と，n回軸に垂直な1つの2回軸を生成元として，完全に決定されます．
技術分野では，対称性n:2は，対称性nと同じような場合に見られます．
記号n:2でnを無限にした極限群は，∞:2　となります．

水晶の主軸に沿って直線偏光が通過するとき，偏光面は水晶内部で右または左に "ねじれ"（左ねじ、右ねじ）ます．右水晶は偏光面を右に，左水晶は左に回転させます（旋光性）．このねじれの向きは，それぞれの水晶で光線を逆行させても同じことです．
しかしながら，磁場中のガラスに見られる磁気的な回転（ファラデー効果）では，光線を逆行させると逆転します．