立体万華鏡

正多面体の二面角は，多角形の頂角のように単純ではありません．凸正多面体Mとその頂点Cを中心とする小球の交差線で，凸球面多角形が形成されます．
頂点Cからq本の辺が出ているとすると，凸球面多角形の辺の二面角の和はπ（q - 2）よりも大きい．
正多面体Mのすべての二面角がπ / 2を超えない場合（たとえば，コクセター多面体の場合），各頂点から出る辺は3本だけであることがわかります．この最後の性質を持つ多面体を単純多面体と呼びます．四面体や立方体は単純多面体ですが，八面体は単純多面体ではありません．

しかし，この単純な不等式だけでは，凸多面体の二面角の関係を網羅することはできません．最も単純なMが三角錐の場合について考えてみましょう．その面に番号をつけ，i 番目と j 番目の面のなす角を α_{ij} = α_{ji} とします．ユークリッド三角錐の二面角が次の関係にあることは，線形代数によって簡単に証明できます．

左辺の行列式は，ピラミッドの面に対する単位法線ベクトルのグラム行列式［ベクトルの内積が成分］で，０に等しいのは，これらのベクトルが線形従属であることによります．二面角αとすると，それぞれの面の垂直ベクトル間の角度はπ-αだから，cos(π-α)=-cosα です．
ユークリッド三角形とすると，α_{12}＝α, α_{13}＝β, α_{23}＝γ　だから，

この簡単な場合からは，α＋β＋γ＝π　が得られます．

関係式(6)は，先に導いた不等式と合わせて，二面角α_{ij}を持つ三角錐がユークリッド空間に存在するための必要十分条件となります．これを利用すると，二面角がπ/整数であるユークリッド空間の三角錐をすべて求めることができ，その数は3つです．図7で，マークのない辺の二面角はπ / 2，マーク|，あるいは，マーク||のついた辺の二面角は，それぞれ，π / 3またはπ / 4です．図7のピラミッドのうち，1つ目のピラミッドを対称面によって切断すると2つ目のピラミッドが得られ，2つ目のピラミッドを対称面で切断すると3つ目のピラミッドが得られます．

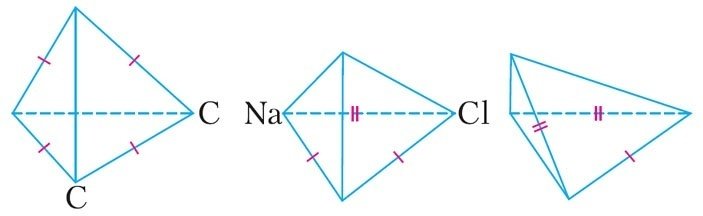
3次元ユークリッド空間には，この3つの万華鏡のほかに，ある意味で2次元に還元された万華鏡が4つだけあります．これは、直角プリズム（3角柱）の底面が2次元の万華鏡であるものです．

3次元ユークリッド万華鏡は，結晶学と密接な関係があります．このような万華鏡の中にいくつかの原子を配置し，万華鏡の壁で繰り返し反射させ得られる像をすべて調べると，結晶格子を得ることができます．つまり，図7に示した万華鏡のうち，1番目の万華鏡で，炭素原子Cを図に示した2つの頂点に置くとダイヤモンドの結晶格子が得られ，2番目の万華鏡で，ナトリウムNaと塩素Clの原子を図に示した頂点に置くと，食塩の結晶格子が得られます．

3次元球面上の万華鏡をすべて見つけることも難しくありません．このすべてが，球面三角錐です．この場合，ユークリッド平面から球面に移るとき，三角形の内角の和がπより大きくなるので，(6)の等号が不等号>に置き換えられます．

引用：
E. B. Vinberg, published in the "Soros Educational Journal" (1997, No. 2)
«КВАНТ» No6, 2020
表紙の写真は「美しい幾何学」p.47より

美しい幾何学