イスラムの皿

東京ジャーミイの玄関ホールの陳列棚に飾ってある美しい皿です．直径30cm程度です．

中心にある大きな花（花弁12枚）の周りに，やや小さい花（花弁９枚）が6個配置されていて，中心に6回回転対称軸があります．
中心の大きな花（花弁12枚）だけ見ると，12回対称です［内部に6回対称の図形が描かれていますが無視します］．これを局所的に12回対称と呼びましょう．
周囲にある６個のやや小さな花（花弁９枚）の1つに注目すると，この部分は9回対称です［内部に５回対称の図形が描かれていますが無視します］．これは局所的に9回対称と呼びましょう．

中心にある大きな花の周囲も含めて全体を見ると，大きな花の中心にあるのは12回対称軸ではなく6回対称軸であることがわかるでしょう．これを全域的には6回対称と呼びます．

一般に，模様の対称性を語るときは全域を支配する対称性のことを言います．この例で見るように，一般に，局所的な対称性は高く，全域に広げるとその対称性は下がります．

実は，このイスラムの皿のデザインは，下図のように周期的に繰り返す壁紙模様からオレンジ色の円の部分を切り取ったものです．

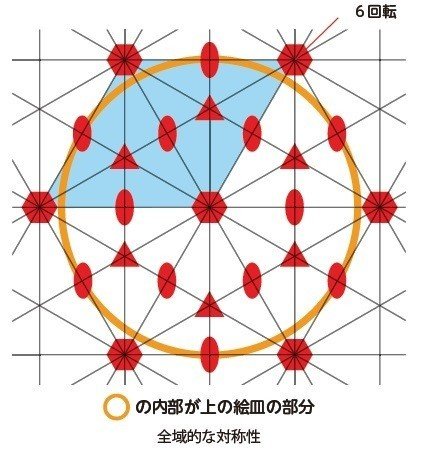
局所的な12回対称軸は全域的な6回対称軸に，局所的な9回対称軸は全域的な３回対称軸になります．さらに，6回対称軸と6回対称軸の間，3回対称軸と3回対称軸の間には2回対称軸が生じています．
その他，図に実線で描いたように鏡映面があります．
図で水色に塗った平行4辺形（正3角形２つ分）が単位胞で，これが繰り返し壁紙模様の単位です．この繰り返し模様は平面群P6mmの対称性です．

■それぞれの花の内部の局所的な対称性
中心の花の内部は，12回対称（その部分群としての６回対称は全域で通用），周りの６個の花の内部は，それぞれ９回対称（その部分群としての３回対称は全域で通用）です．
繰り返し模様の全域で通用する対称性に，12回対称や９回対称はあり得ません．何故かというと，正12角形（あるいは正9角形）のタイルで平面のタイル張りはできませんから．平面を隙間なく張り詰められる正多角形タイルは，正3,4,6角形タイルです．正5角形タイルでも張り詰めることはできません．12回対称や9回対称のような高い対称性が通用するのは，それぞれの花の内部だけ（局所的）で，周期的な世界全域で通用するものではありません．イスラムの模様の特徴は，局所的に高い対称性の星形がちりばめられていることです．あたかも，高次元宇宙のいろいろな断面が２次元の皿の表面に投影されているようで，不思議な魅力を感じます．

美しい幾何学p.178より

美しい幾何学