19世紀の科学業績ーマクスウェル方程式

20世紀の科学的発見で，最も偉大な業績とされるべきものは何でしょうか．おそらく，量子力学の誕生でしょう．量子力学は，ミクロの世界（原子や粒子のレベル）で起こることを説明するだけでなく，トランジスタやレーザー，超伝導や原子工業など，新しい技術を生み出したのです．
ちなみに，数学者は，量子力学を記述するための適切な数学ツールを開発し，量子力学に大きく貢献しました．水素原子に関する最初の量子方程式は，シュレーディンガーの依頼で数学者ワイルが解きました．
同様の問いを19世紀の科学についてすれば，答えは明白．マクスウェルの方程式を中心とした電磁気学の誕生である．
もちろん，ここでも熱力学や統計力学の創始などの他の目覚ましい成果も忘れてはならない．しかし，マクスウェルの方程式によって電気を「制御」する時代が到来し，蒸気の時代から電気の時代に引き継がれたのだ．
電気力学の分野では，マクスウェルに先立ち，エルステッド，アンペール，そしてもちろんファラデーという優れた先達がいた．彼らは，電気力学の基本法則を実験的に確立していた．彼らは，誘導電流，磁力線，自己誘導現象などを発見した．しかし，この分野で最も印象的な功績は，「場」の概念を導入したことだろう．電気や磁気は，いわば空間のすべてに「浸透」している．空間に「プローブ」としての電荷や電流がなくても，電場や磁場は空間に存在している．電場や磁場という２つのベクトル場は，空間座標および時間に依存する．マクスウェルは，実験結果をもとに，これらの場が従う方程式系を導き出した．

この方程式ができるまでの道のりは，実に長いものだった．
というのも，適切な力学的アナロジーを見つけるのに長い時間がかかったからである．
トムソン（ケルビン卿）とマクスウェルを導いた主なアイデアは，理想的な非圧縮流体の渦流のアナロジーだった．電場や磁場は，流体で質量のない物質，つまり最も希薄なエーテルであり，空間全体を満たし変動するものと考えられていた．

$${\displaystyle \frac{ \partial H}{ \partial t}=-c  \textrm{rot}E}$$, $${\textrm{div}H=0}$$

$${\displaystyle \frac{ \partial E}{ \partial t}=c  \textrm{rot}H}$$, $${\textrm{div}E=0}$$
*訳者注）$${ E(x,y,z,t), H(x,y,z,t)}$$は，それぞれ電場ベクトル，磁場ベクトルで，空間の座標と時間の関数．$${ \textrm{rot}E}$$や$${ \textrm{div}E}$$は，それぞれ，ベクトル場での回転，発散と言われる演算でベクトルを出力する．

このアイディアは，有名な数学者デカルトに遡る．彼は同様の基礎の上に物質の渦理論を構築しようとしました．機械的なアナロジーは発見的な目的を果たしたが，現代の電磁気学の教科書には今やその痕跡すらない．しかし，方程式そのものに，回転rotと発散divという形で，渦と非圧縮性に関する響きが残されている．
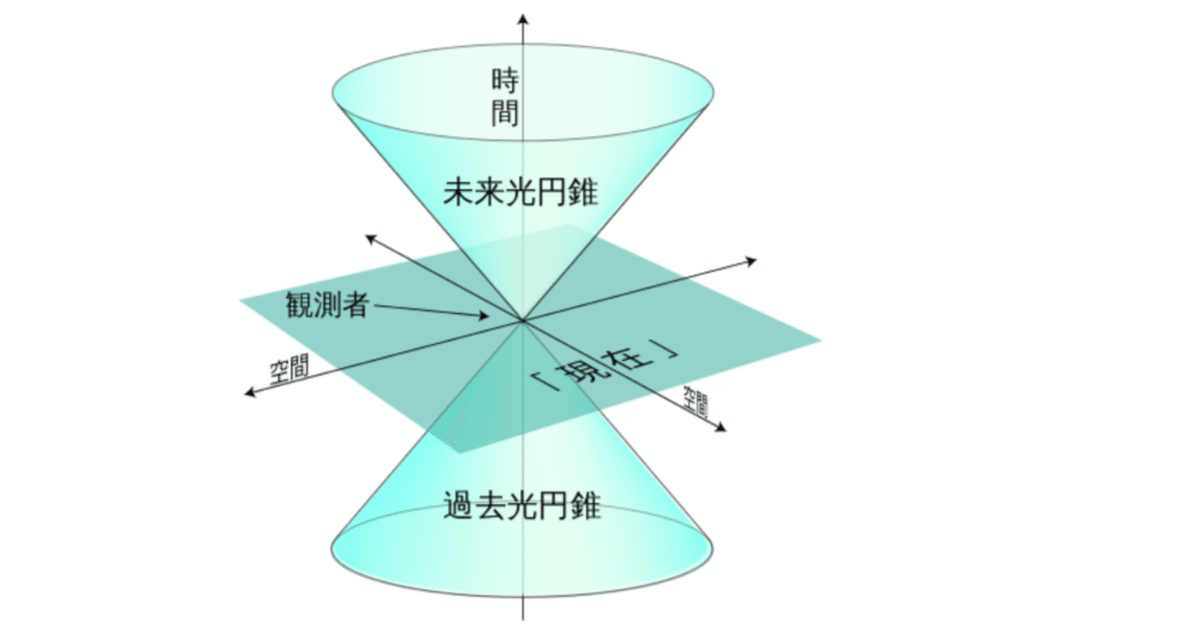
マクスウェル方程式は，電気通信技術の発展と時空に関する現代物理概念の形成に，基本的な役割を果たした．これにより，光の電磁気的性質が明らかになり，1888年，ヘルツは電磁波を発生させる方法を発見した．その直後，ポポフやマルコーニがヘルツのアイデアを利用して，遠距離の無線通信を実用化した．マクスウェル方程式のもう一つの重要な帰結は，相対論的力学である．ポアンカレがローレンツ群と呼んだ4次元時空の線形変換の10個のパラメータ群に関して，マクスウェル方程式はその形を保つことが判明したのである．一方，3次元空間におけるニュートンの第2法則の方程式は，同じく10個のパラメータに依存するガリレオ変換群を許容している．相対論的力学の基本的な考え方は，力学と電気力学を調和させるために，ガリレオ群をローレンツ群に置き換えるべきだというものだ．相対論的力学の考え方は，現代の空間と時間の理解を形成し，マクスウェル方程式は電気力学の数学的基礎となっただけでなく，世界の物理的全体像の整合性を維持することを可能にした．

引用：МАТЕМАТИЧЕСКАЯ СОСТАВЛЯЮЩАЯ 
Редакторы-составители Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин
p.30-31