定規とコンパスで作図できる長さ

私は，yahooブログ 「数学と社会の架け橋<数学月間>（2012.5～2019.3）」に，発行している同名のメルマガまぐまぐのバックナンバーを保存していました．メルマガはテキストなので，必要な図はどこかに保存したもののリンクを張らねばなりません．そこで，必要な図や写真はyohooブログに保存していました．しかし，昨年yahooブログが閉鎖しましたので，ブログ機能はlivedoorブログと数学月間の会のホームページに引っ越しました．
テキストは移動できたのですが，移動できなかった画像や写真があります．yahooブログに張ったリンク先が消えてしまったので後の祭りです．
今回Noteを始めて，それらの記事中から面白いものを優先し，図を作り直し再現しようとしています（新規の記事も並行して随時書きます）．お付き合いのほどよろしくお願いします．記事の候補全体は，数学月間の会ホームページにありますので訪問ください．その中で再現すべき記事のリクエストがありましたらお寄せください．まだNoteの使い方になれないので皆さまのお気づきのことをお教えください．記事に数式が必要なこともありますが，Texが使えないようなので，まとまった数式は画像にして埋め込むことにしています．

今回再現するのは，以下のメルマガの記事です．
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2018.10.23］ No.238
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
今日は，たいへん古典的だが，重要な証明問題を扱いましょう．
ギリシャの幾何学者達が研究した不可能作図とは
以下のものがあります．

（１）与えられた立方体の2倍の体積の立方体を作れ
（２）与えられた円と同じ面積の正方形を作れ
（３）任意に与えられた角を3等分せよ
これらは，定規とコンパスだけを有限回使って作図できるか？
ということです．

■なぜ作図できないか
（１）は，2の3乗根の作図が必要です．
（２）の円と同じ面積の正方形を作る方針を以下の図に示します．

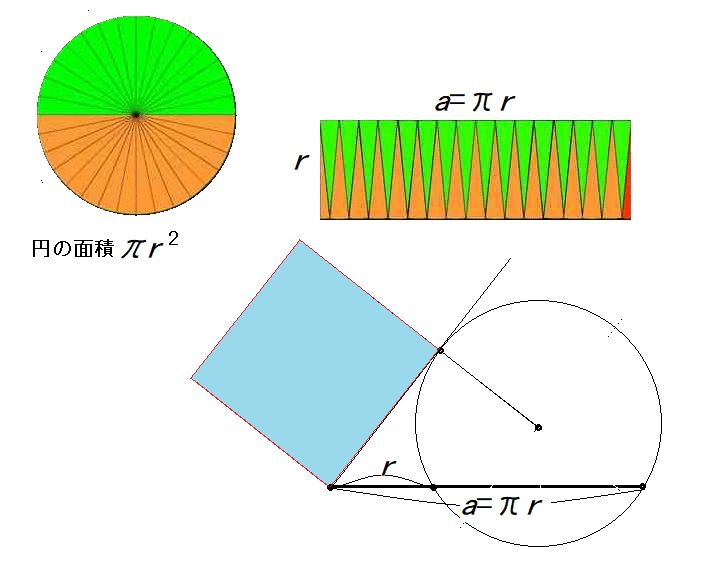どうしてこの作図ができないのかわかりますか？
与えられた円の半径をrとします．まず，円と同じ面積の長方形を作りましょう．もし，縦r，横aの長方形が作れたら，r･a=x^2　となるxの作図は可能です．問題は，円の面積と同じ縦 r，横 a=πｒの長方形を作るところで，
円周の半分の長さπrの線分を作図する方法が，定規とコンパスではないからです．無理数πが作図できません．

■直線定規とコンパスだけを有限回繰り返し用いて作図できる長さは
２つの有理数の，加法，減法，乗法，除法，開平だけです．
作図方法は，以下をご覧ください．
条規とコンパスで作図
開平を繰り返せは，2のべき乗根（4乗根，8乗根，．．．）は作図できますが，例えば，立方根は作図できません（この証明は難かしいのでスキップ）.

（３）任意の角度の3等分が作図できないわけ．
角度3等分の方程式は　x^3-3x-a=0　で，
例えば，与えられた角度が60°ならa=1の方程式です．
60°の3等分の方程式は，x^3-3x-1=0　となりますが，この3次方程式は，p+q√r　（ただし，p,q,rは有理数）の型の解を持たないので
この角度の作図は，定規とコンパスでは不可能です．
もちろん，60°の3等分の20°は存在しますが，
定規とコンパスだけを使う方法では作図できないということです．
詳しくは，以下をご覧ください．

■任意の角度の3等分
任意の角度∠XOYの3等分がなされたとします．

■２の4乗根の作図

△ABCはAC＝BC＝１の直角3角形．従って,AB＝√2．
点Aから線分AB上にAD=1の点Dをとる．

DBの垂直2等分線上に中心のある円で，点Dや点Bを通る円を描く．
あとは，この円でほうべきの定理を使う．つまり，点Aからこの円への接線APを引けば，AP^2=AD･AB＝1･√2　だから，APは２の4乗根になる．