ネットワーク・パターンの対称性2
点の対称性は∞・mと仮定します.この記号の意味は,紙面に垂直な∞回転対称軸(回転対称の極限)とその対称軸を含む鏡映面mがあるという意味です.理想的な点は,その点を通り紙面に垂直な軸のまわりに任意の角度回転しても,あるいは,この回転軸を含む任意の面で鏡映させても,始めの点と一致するというものです.
1つの点を平方移動したものを集めた集合を点系(同価な点の集合)と呼びます.
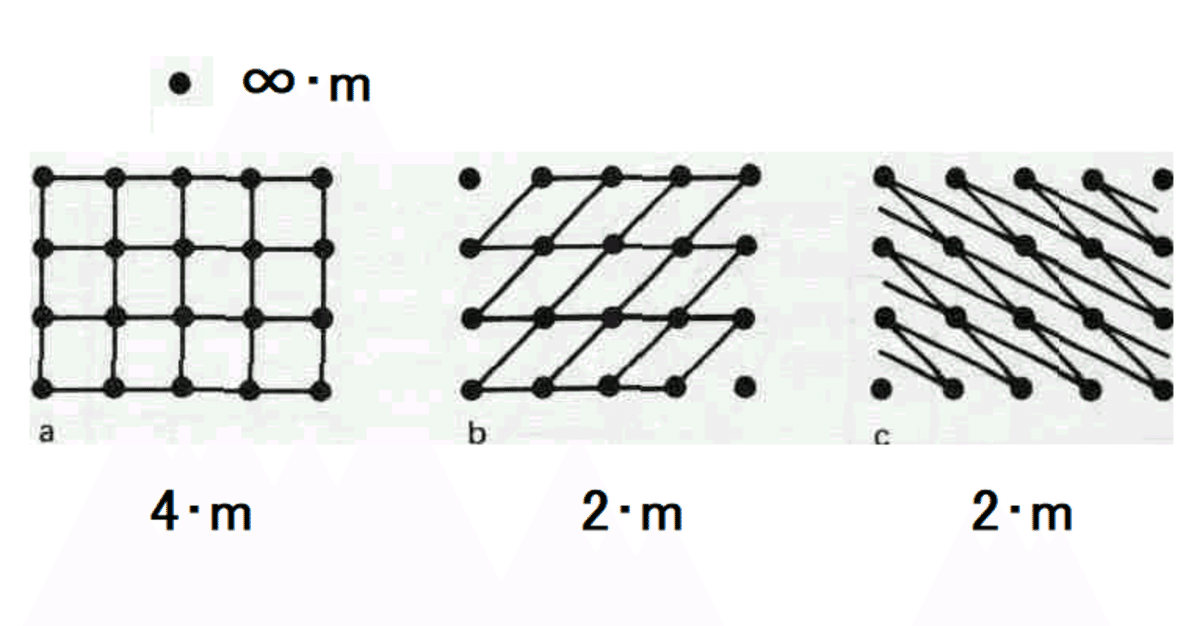
点系の全体の対称性は,点の配置に依存しており,孤立した一点の対称性とは同じではありません.この様子を表紙の図でご覧ください.点だけの配置なら,図の3つの点系ですべて同一,対称性4・m(この記号の意味は,紙面に垂直に4回回転対称軸があり,この軸を含むような鏡映面がある)です.いずれかの点を通る軸の周りに90°回転したり,その対称軸を含む面で鏡映させても,固定点も系全体もそれ自身と一致します.しかし,正方形のネット(図左a)だけが,その構造の基礎となっている点系と同じ対称性を持ちます.つまり,ネットと点系の両方が,点と正方形の中点を通る4回回転軸,正方形の側面の中点を通る2回回転軸,垂直な対称面などを持っています.同じ点の系から作られた他のネット(図中9b,図右c)では,例えば,4回回転軸や垂直対称面がないなど対称性が異なります.点系からネットを作るとき,その点系と同じ対称性を持つネットの作り方(上の例では,図左a)を選ぶことにします.
各点で,2本(2本だけ)の直線が交差するように点が結ばれ,かつ,直線が点の位置でのみ交差するように点が結ばれていれば,結び方がどのようなものであっても,結果として得られる平行4辺形は同じ面積を有し,例えば,表紙の3つの図では,各平行4辺形の面積は全部同じ,図左の正方形の面積と同じです.このように構成された平行4辺形は,その辺の長さa,bと,これらの辺の間の角度α(a軸とb軸の正の方向の間の角度)によって規定される.これらの平行4辺形をネットの単位メッシュを「単位胞」(単位格子という言葉は避けたいと思います)と呼び,量a, b, αを格子定数と呼びます.
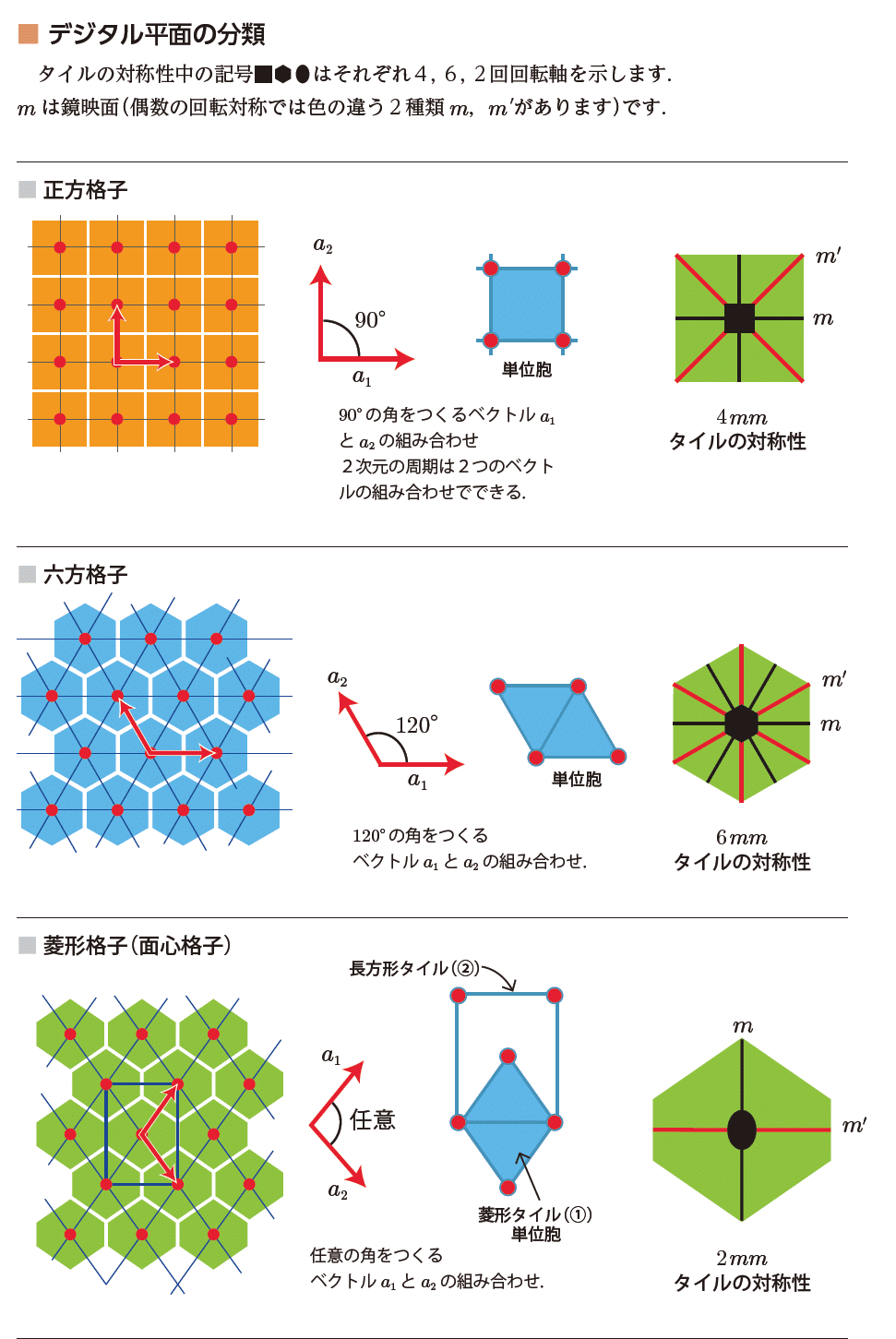
メッシュ(格子)の平行4辺形を,格子定数の対称性で分類すると,2次元では5種類になります(2次元のブラベ格子といいます).
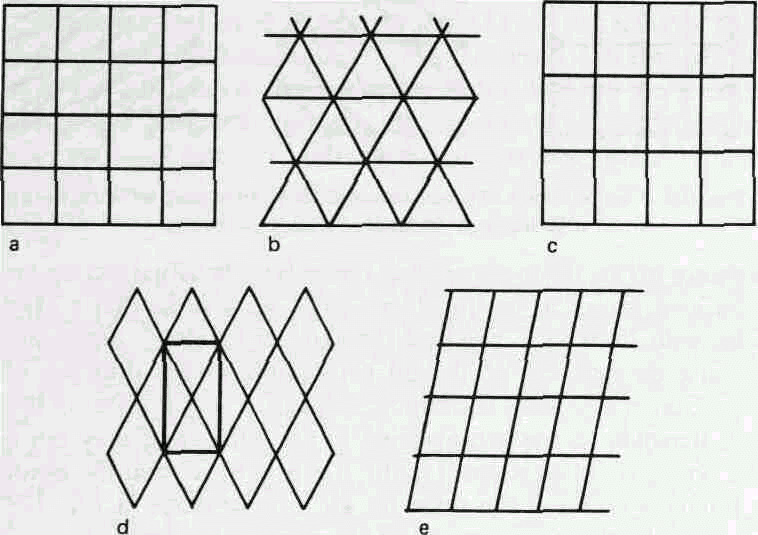
(a)正方格子 対称性4・m 格子記号(a:a) b=a,α=90°
(b)3方格子 対称性2・m 格子記号(a/a) b=a,α=60°
6方格子
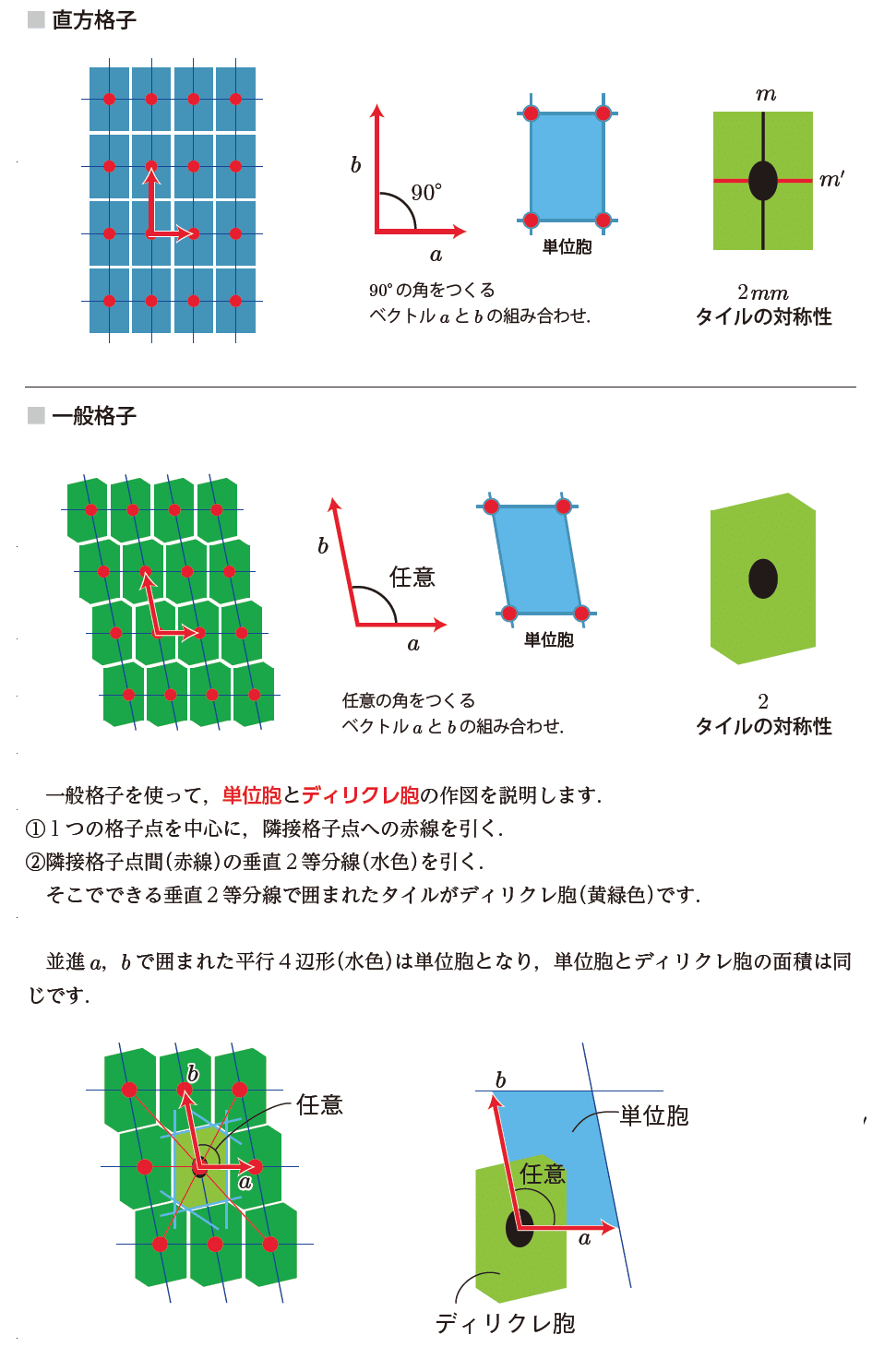
(c)直方格子 対称性2・m 格子記号(b:a) b≠a,α=90°
(d)面心直方格子 対称性2・m 格子記号(c/b:a) c=(a+b)/2,b≠a,α=90°
菱形格子 2・m (a/a) b=a,α≠90°,α≠60°
(e)斜平行4辺形 対称性2 格子記号(b/a) b≠a,α≠90°
美しい幾何学p54,55
