
成長は毎日の「1%の積み重ね」
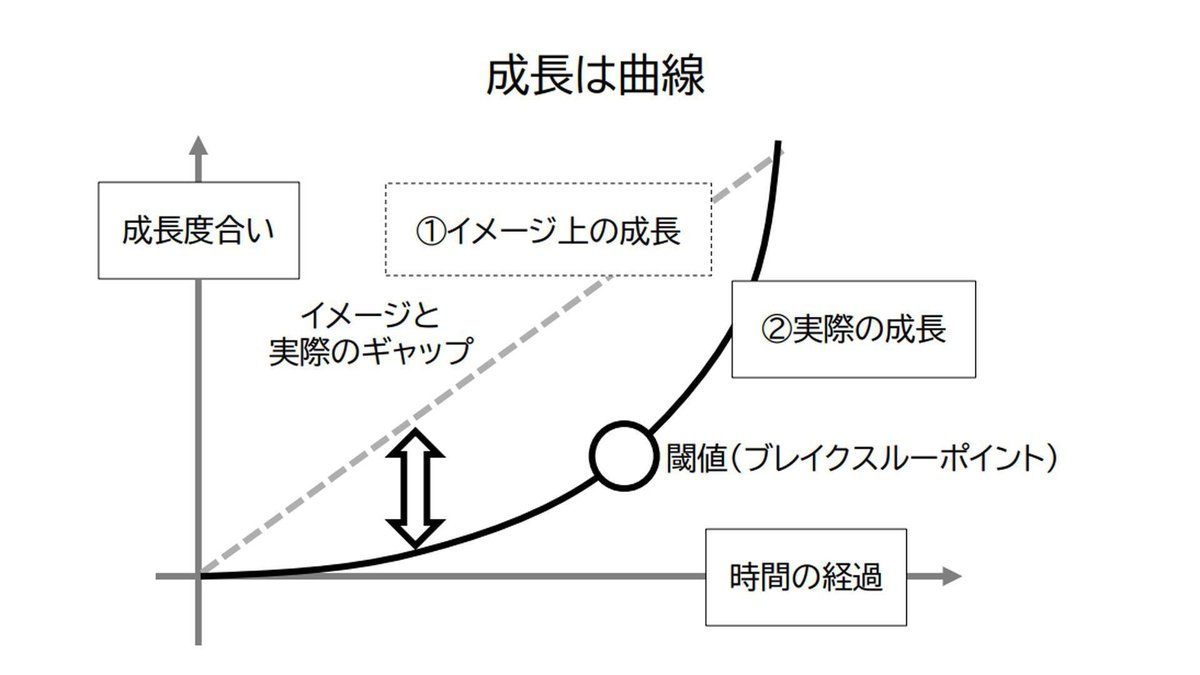
多くの人は「成長は正比例の直線」(①の直線)と思っていますが、「成長は複利計算」ですので「反比例の曲線」(②の曲線)を描いて上昇していきます。

複利計算とは、例えば「毎日1%ずつ成長する」とした場合に「1.01 の累乗(べき乗)」で計算されることとなります。(成長は複利計算の表参照。)
・1日では 1.01
・2日継続することで 1.01 の2乗=1.0201
・3日継続することで 1.01 の3乗=1.0303
というように、最初のうちは目に見えないくらい緩やかに上昇して行きます。
多くの人は「成長は正比例の直線」をイメージしていますが、実際は「反比例の曲線」のため、イメージと実際の成長の「成長ギャップ」を感じ、「イメージとおりに成長していない」と感じてしまうため、取り組みをやめてしまうことも生じます。
大切なことはやり続けること
で、
「閾値(いきち・しきいち)」と呼ばれるブレイクスルーポイントを超えると成長を実感することができるようになります。
取り組み方が異なるので、人によって、習慣化に必要な期間(ブレイクスルーポイント)は異なります。
ちなみに・・・
ユニバーシティ・カレッジ・ロンドン(UCL)で行った調査で、21歳~45歳の学生96人に、毎日できそうだが実際には行っていない行動を1つ選んでもらい、その行動を行ったか毎日ウェブ上で報告してもらったところ、「被験者の習慣化に必要な日数の平均値は 66日」という実験結果が出ています。
※How are habits formed: Modelling habit formation in the real world
(習慣はどのように形成されるか: 現実世界での習慣形成のモデル化)
First published: 16 July 2009,Phillippa Lally
「成長は複利計算」ですが、注意点があります。
1日休んだ場合には「ストレス」を感じることとなり、「0.9」などの成長を打ち消す数字をかけ算することになってしまいます。
行動を継続することが大切です。
また・・・
逆に「マイナス」にも「成長は複利計算」は当てはまります。
毎日ジワジワと「マイナス成長」をしていき、閾値を超えた途端に事象となって現れ、氣づいた時にはマイナスが止められなくなり「手遅れ」となる場合もあります。
単純にプラスに成長するのか、マイナスになるのかのどちらかではなく、
・とある日はプラス
・別の日はマイナス
のように推移していきます。
成長は行動し続けることにより実現するものなのだと感じます。
