政経たんが数学を難しく考えない話
文系の方が理系学問をやるために数学の壁にぶつかるの、理系の人が文系学問やろうとして(英語以外の)外国語の必要性を迫られるのに似ているのでは。
— 科学哲学たん (@kagakutetsugaku) June 28, 2020
お互い日本語の範疇なら所詮教養レベルということで、未履修を咎めるのはやめましょう。
おそらく、それでも文系への「数学で厳密にやれ」という批判は、少なくとも高校までは全員が数学をやっているという事実前提のせい。
— 科学哲学たん (@kagakutetsugaku) June 28, 2020
とがめられることあるんですか? 色々やっていてどうしても数学にぶち当たることはありますし、どうしても外国語にぶち当たることはありますね。
— 政経たん@VRアカデミア見習い (@Seikeitan) June 29, 2020
それ以上でもそれ以下でもない…かも?
私から見て特に目立つのは、物理学をやらずに哲学で時間だの宇宙だの語られる人の場合ですかね。。
— 科学哲学たん (@kagakutetsugaku) June 29, 2020
すでに科学的に確かめられた事実があるのに、それを勉強せずに自分の経験と直感だけを信じて哲学をやる人、たまにいるよね…
— 視点学たん(viewpointics-tan) (@viewpointicstan) June 29, 2020
(哲学も数学Aで学ぶベン図とか使うはずなのですが、)そのような方々いるんですね。神のサイコロを振りもせず。
— 政経たん@VRアカデミア見習い (@Seikeitan) June 29, 2020
みなにありうることですが、自分の見識だけしか信じないことはありますよ。正直、話が無限後退しちゃいますが。
— 政経たん@VRアカデミア見習い (@Seikeitan) June 29, 2020
ところでこれらのツイート、大変興味深いのでnoteに使いたいのですがよろしいですか?
色々思うことはありますが、数学とは大変難儀なものです。
私は文系ではありましたが、旧数学ⅢCまで履修してしまうということをしました。とはいえそれでも今となっては、やってよかったと思うことは多々あります。おそらく数学に限らずどの学問でもそうですが、その先の大学生が学ぶような内容を、それほど抵抗なく聞くことができるようになりました(偏微分や重積分など)。成績はよくありませんでしたが、数学ⅢとCで「いよいよのところまで学んでいる」という実感はありました。数学Ⅲは延々と微分積分、数学Cは行列式をやりました。
数学…拒否反応はない(つもり)けど、やはり私の専門分野および領域からしてもちろん理科系の人よりは、処理や理解に時間かかる。そしておでこあたりが痛くなる。
— 政経たん@VRアカデミア見習い (@Seikeitan) June 29, 2020
とはいえ、本業の方よりは遥かに数学に関わらないので、もちろん弱いです。私が学部で専攻した経済学も、難しくて中学数学程度であった記憶があります。そもそも数学で入試を受けていない人も多いと思います。
さてここから本題に移ります。
数学が苦手な方というのは、おそらく中等教育(中高)の数学ですっかり嫌になったという方は圧倒的に多いでしょう。
以下、持論が多くなることをご容赦ください。
おそらく、苦手な方は数学のイメージや概論がまったくつかめていないのではないでしょうか。
で述べたとおり、
私が申し上げたいのは、あまり具体的な事象に惑わされず、「概ねどのようなものなのか?」「そもそもどんなものなのか?」という感覚を忘れないでほしいということです。
に尽きます。
日本の数学の教科書は、内容としてはとてもいいものだそうです。ですが、その教え方や記述に問題があると私は見ています。
ところで、皆さんは三角形を御存知ですよね?
馬鹿になんかしていません。そして皆さんは三角形の面積の出し方を知っているはずです。

「テイヘンカケルタカサワルニ」ですね。
では円の面積の求め方はわかりますか?
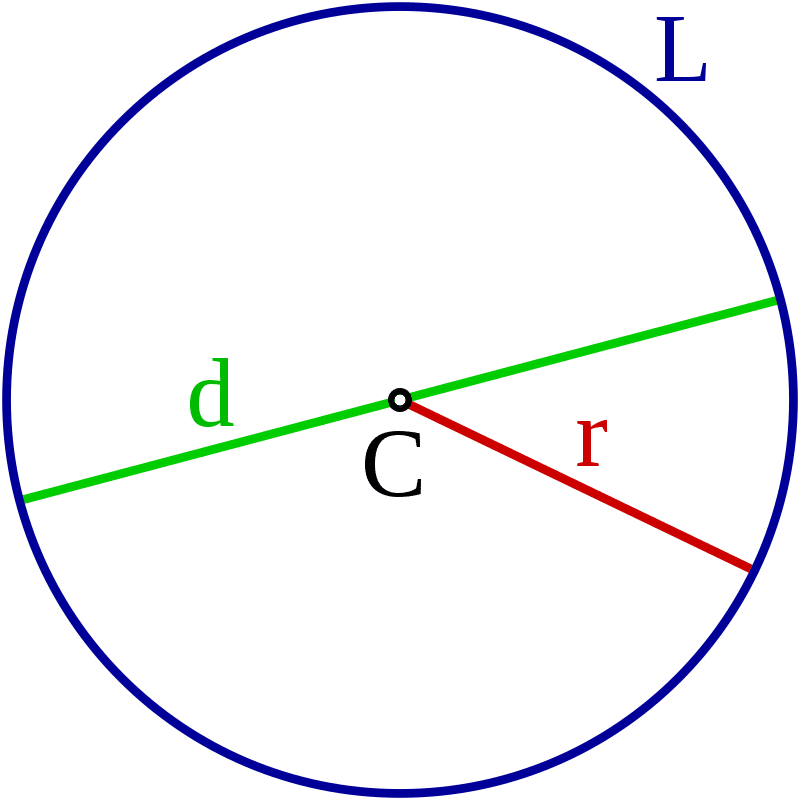
「ハンケイカケルハンケイカケルサンテンイチヨン」ですね。
「パイアールジジョウ」で憶えている方もいるでしょうか。
あえてカタカナで書いたのは、ちょっとここに問題があると見ているからです。
ここで台形の面積の出し方を見てみましょう。

一時期台形の面積の求め方が騒がれましたが、多くの方は「ジョウテイタスカテイカケルタカサワルニ」で憶えているのではないでしょうか。
早速ここでも、ちょっと問題を見つけることができます。
詳細は↓でわかります。
台形の面積の公式
乱暴な言い方をすると、台形の面積の出し方と三角形の面積の出し方は同じです。
上底と下底を底辺とみなすと、結局「底辺×高さ÷2」になるのです。
なんとなく私の言いたいことがわかってきたのではないでしょうか。
「台形とはどんなものなのか」「三角形はそもそも四角形の面積の出し方の延長線上にある」という「意味」を教えることがもしかしたら欠落しているのではないか、と思えるわけです。
何も小学生すべてにそう教えよとは言いません。ですが躓く子はそういうところで躓いている可能性は大いにあると考えます。それで数学嫌いになってしまうなんて、むしろ損失とさえ言えるのではないしょうか。
話を戻します。(ここから積分という単語が出てきますので、読み飛ばしたい方は読み飛ばしてください)
円の面積と三角形の面積ですが、これは実は積分なんです。
「えーっそんなの知らないよ」という方が多いと思いますが、そもそも面積を求めるという計算は極めて数学的な行いです。
それについてのサイトを掲示しておきます。
6. 面積・体積の算出に見る「瞬間を捉える」というアイデアの凄さ
https://gakuen.gifu-net.ed.jp/~contents/museum/infinity/page82_6.html
みなさんも中学生や高校生のとき、数学をやっていて「なんかこれ前に出てこなかったかな」「前にやったことをなんでもう一度やるの?どういうこと?」ということは多くなかったでしょうか。例えば連立方程式と一次関数の交点の求め方はまったく同じで、そもそも関数の式は方程式ですので、当然といえば当然です。2次以上になるとx軸やy軸と交わらなくなる場合があり、それが「虚数解を持つ2次方程式の解」ということになるます。さらに言えば、「方程式の解を求めることとは、座標軸においてx軸との交点を求めること」ということです。
さて、色々異論を唱えられそうな記事になりましたが、最終的に言いたいことは、「具体的な数式を経ずとも、概略を捉えることは可能ではないか」ということです。逆に言うと数式はそれこそ文字通り記号のようなもので、それを噛み砕き翻訳することが重要とさえ思います。
「今になってそれいうなよ・・・」「中高のときに知りたかった」という人もいるかもしれません。でも気に病む必要もないでしょう。何もいつ学んで遅いということはないでしょうし、知の幅が広がるのはいいことです。もし周りに中高生がいれば、そっと教えてあげるのも、もしかしたら大人の役目とさえ言えるのかもしれませんから。
この記事が気に入ったらサポートをしてみませんか?
