
機械学習を用いたイルルカSPモンスターの分類(1)
概要
イルルカSPには903種類ものモンスターが存在し、各々が異なる性質を持っている。これらから何匹かを選択し、対戦に用いるモンスターを決める訳であるが、この膨大な数からこれを行うのは極めて困難である。そこで、どのモンスターとモンスターが類似しているか分類することによって、その労力を軽減させるということを考える。それに適した手法として機械学習、特に教師無しのものが挙げられる。本稿では機械学習を用いてイルルカSPに登場するモンスター間の類似性を計算し、対戦に臨むユーザーの助けとする。読者層を鑑み、正確性よりも機械学習に馴染みのない人への分かり易さを随所で優先した。
背景
イルルカSPプレイヤーの思考と機械学習の必要性
イルルカSPでは、日夜、様々なルールによる対戦が行われている。任意のモンスター、スキルが自由に使える通常のルールの他、使用出来るモンスターやスキルに制限を加えた私人間で企画された対戦会も度々行われている。
そのような場合に、プレイヤーは自分が使用するモンスターをどのように選んでいるであろうか。大抵の場合、特性や耐性に一定の要件があり、その条件を満たす中から最もステータスも含めた他の条件が用途に合っているものを選ぶのではないだろうか。例えば「状態異常耐性の高いスモールボディのモンスターが欲しい」というような条件があって、それを満たすものとして妖魔軍王ブギー、AI3新生ぶちスライムベス、スモボ化メルトア、スモボ化大魔王マデュラージャ、スモボ化真・魔王ザラーム等が候補として挙げられてきて、その中で最も今の自分にとって都合の良いもの(リバースパーティならメルトア、黒霧パーティならマデュラージャ、凍てつく波動が欲しいならザラーム、3回行動とより鉄壁の異常耐性ならぶちスライムベス)が選ばれるという風にである。
ここで重要なのは「状態異常耐性の高いスモールボディのモンスターが欲しい」というような、有用なモンスターを探す為の条件設定がどのようにして決まっているかである。例えばこれが「メラ系のコツと炎ブレスブレイクを同時に持つモンスター」だった場合、マグマスライムやフレイム、ようがんまじん、かりゅうそう、スライムタール、バラモス等が該当するが、彼等が「状態異常耐性の高いスモールボディのモンスター」で出てきたモンスターより有用だと考える人は少ないであろう。メラ系のコツと炎ブレスブレイクの両立は特技の火炎竜を最大限に活かせる特性の組み合わせであり、意味のない探索条件ではないにも関わらず、である。他にも「マインド耐性が高めで暴走機関の特性を持ち、攻撃力の高い1枠モンスター」という条件だと、ドラゴンマッド、せつげんりゅう、コングヘッド、あらくれチャッピー、アンドレアル、キラーマジンガ、レオパルド、デモンスペーディオ等が見つかる。キラーマジンガやレオパルド、デモンスペーディオは今でも一部の構築に使われるものの、それでもこの探索条件がイルルカSPにおいて優れているとまでは考え難いのではないだろうか。「メラ系のコツと炎ブレスブレイクを同時に持つモンスター」よりは有益な結果であろうが、「状態異常耐性の高いスモールボディのモンスター」には劣っている。
以上の議論において、探索条件から得られたモンスターを見て自然と彼等が強いのか弱いのか特に議論もせずに判断していたが、その判断について、イルルカSPで日々対戦を行っているような者にとってはほぼ自明、そうでないものにとっては意味不明であろう。それでいて、対戦を行っている者がそうでない者に対し、その判断の正しさの根拠を説明せよと言われたら、殆どの者が相手に納得させるのに失敗するのではないだろうか。仮にそうなると仮定した場合、「対戦者はモンスターの強さを過去の対戦で高頻度で使われて結果を出しているかどうかで判断している」という仮説を立てることでこれを説明することが出来る。過去の対戦でどうだったかという経験は対戦者にとっては共有された知識であるが、そうでない者にとっては知らないことであるし、これを理屈で説明するのは難しい。そして頭で考えた理屈ではなく過去の実績を基に判断しているからこそ、環境の変化に対してプレイヤーが適応している現実を説明出来る。「マインド耐性が高めで暴走機関の特性を持ち、攻撃力の高い1枠モンスター」という条件は3DS版でGPにおける優勝を狙っている場合には最重要な探索範囲であったが、これが何故SPの段位戦ではそれと比べれば重要性が落ちるのか、その判断は2つの対戦環境の違いを列挙するよりも、SPの段位戦における実績を出す方が多くのプレイヤーは納得する筈である。
この仮説を真と認めた上で議論を進めると、「状態異常耐性の高いスモールボディのモンスター」という探索条件が優れているのは、その条件を満たすモンスターに対戦で活躍したことのある種族が多いからということになる。そこから次のような仮説が立つ。即ち、「対戦するプレイヤーは対戦で過去に活躍したモンスターから共通点を探し、同じ特徴を持つモンスターを強いモンスターだと判断している」であろうと考えることが出来る。これはパーティの改良の過程にも整合的で、それなりに妥当性のあるものであろう。具体例としてシャフ黒リバ(下記参照)の発展の歴史的経緯を確認してみよう。
シャフ黒リバは松山研斗によって考案された当初、表にスピンスライム、はぐれメタル、大魔王マデュラージャ、デモンスペーディオ、裏にどんぐりベビー、マジェス・ドレアム、妖魔軍王ブギー、メルトアを置くという形であった。次にXepalousが(恐らく)「異常耐性を上げる為にウルトラガードSPが必要なデモンスペーディオは使える特技がその分少なく、光の波動や精霊の歌、ザオリク、ゼロの衝撃程度ではAI3回という行動回数を持て余しがちである。大魔王マデュラージャを回復役に回せばウルトラガードSPが不要なのでその分別のスキル(メタル潰し)を入れることが出来るし、行動回数がAI2~3と若干落ちても大して困らないであろう。抜けた攻撃役には新たにAI3新生ぶちスライムベスを加える。異常耐性の高さも行動回数も大魔王マデュラージャに勝るので問題無く運用出来るだろう」と考え、表がスピンスライム、はぐれメタル、ぶちスライムベス、大魔王マデュラージャとなった。そしてメタル潰しを採用した目的である身代わり封じや仁王斬りは実際にはあまり活用することが少なかったというXepalousの経験談を踏まえて、私は「このパーティの表は蘇生と異常回復は出来るがHP回復が出来ないのが欠点であったので、身代わり封じが要らないのであればメタル潰しは魔戦車ダビドに変えよう。アモールの雨でHP回復が図れるようになる。メタル潰しには黒い霧も入っていてチェイン対策には便利ではあったが、魔戦車ダビドにもラウンドゼロがあり、チェインだけでなくパーティチェンジ対策にもなる。そしてマインド耐性を過剰にすることが出来、異常攻めに対しより堅牢にもなる筈だ」と考え、大魔王マデュラージャのスキルを変更した(余談であるが、この時同時にXepalousから表に轟雷滅殺剣は2つ以上あった方が良いとも助言を受けており、ぶちスライムベスから戦場の支配者SPを抜くことで、現在では定番の1つであるマジェス・ドレアム、チャンピオンSP、ブオーンのスキル構成に至っている)。今度はデロトが「ラウンドゼロをチェインやパーティチェンジ対策のみに使うのは勿体無い。大魔王マデュラージャをスタンダードボディではなくスモールボディにすればより多くの場面で相手を縛ることが出来る筈だ。裏のAI3新生どんぐりベビーは行動回数の多いスモールボディであるが異常耐性が高くない。表にスモボ化真・魔王ザラームを入れ、ぶちスライムベスを裏に回せば異常耐性を上げられる。真・魔王ザラームは未だ他のパーティにおいても運用実績が無く、行動回数もAI2~3でAI3新生ぶちスライムベスより少ないものの、大元の松山研斗時代には同じくAI2~3(かつヘロヘロや強者の余裕で実際には更にもう少し行動回数が減る)の大魔王マデュラージャが攻撃役をしていたのだから、これでも問題は無いだろう。真・魔王ザラームは凍てつく波動の特性があるのでチェイン対策として裏ではなく表に置く」と考え、表がスピンスライム、はぐれメタル、真・魔王ザラーム、大魔王マデュラージャ、裏が妖魔軍王ブギー、ぶちスライムベス、マジェス・ドレアム、メルトアとなった。更にその後、並行してシャフ黒リバを研究していたニートが「はぐれメタルの強みは第一に素早さである。そうであるならば、より素早さの高いはぐれメタルキングやいきなりピオラのあるシーメーダはより優秀な筈である。異常耐性が高いモンスターが多く採用され邪竜神の叫びや絶対零度の信用が落ちている今、シーメーダによる斬撃・体技封じの息はより有用である」との考えに基づきはぐれメタルがAI3新生シーメーダに置換されつつあり、デロトもそれに則ってシーメーダを採用した。また、妖魔軍王ブギーがメガザルダンスや異常撒き、体当たりや特攻以外の仕事を熟し難いことを受け、デロトは常にアタックカンタとマホカンタを持つスモボ化闇竜シャムダに創造神マデサゴーラを持たせた個体をブギーの代わりに採用し、予測や強風等を使うようにもなった。これが私の把握している範囲におけるシャフ黒リバの発展の歴史である。
以上の歴史において、
デモンスペーディオの代わりに大魔王マデュラージャも回復役になれる
大魔王マデュラージャの代わりにAI3ぶちスライムベスも攻撃役になれる
AI3ぶちスライムベスの代わりに真・魔王ザラームも攻撃役になれる
妖魔軍王ブギーの代わりに闇竜シャムダもメガザルダンス役になれる
とそれぞれのプレイヤーが考えたくだりは、何れも今まで活躍してきた実績のあるモンスターとの共通点(これらの場合は異常耐性と行動回数、更に加えてブギーとシャムダの場合は高いHP)によって新しいモンスターも運用可能であろうという推論が為されている。これは「対戦するプレイヤーは対戦で過去に活躍したモンスターから共通点を探し、同じ特徴を持つモンスターを強いモンスターだと判断している」という仮説に対し整合的で、その傍証となっている。AI3はぐれメタルの代わりにAI3シーメーダを採用するというのも、行動回数と素早さの高さに共通点を見出し、その上でより高い素早さ、より高い妨害性能を評価してのことであり、注目する点こそ異なれど共通点を見つけていることには変わりない。その他、AI3ぶちスライムベスに戦場の支配者SPではなくマジェス・ドレアムのスキルを採用し、轟雷滅殺剣の数を増やした方が良いというのも、似たようなシャフ黒構築同士で戦った際に轟雷滅殺剣の枚数の多いパーティの方が強く、そちらに似ている方が良いと考えているのだと解釈すれば、やはり共通点、類似性の話となる。回復役の大魔王マデュラージャのスキルをメタル潰しから魔戦車ダビドに変更し、黒い霧を失う代わりにラウンドゼロを得るというのも、どちらもチェイン対策になるという共通点によって肯定されている。
尤も、当然ではあるが、パーティ構築における思考の全てが過去との類似性に基づいて行われる訳ではない。回復役の大魔王マデュラージャにアモールの雨を覚えさせてHP回復も行わせようというのは、元々シャフ黒がHP回復無しでも成立していたことを踏まえると前例との類似性では説明し難いことである(尤も、シャフ黒以外にも目を向け、多くの強い構築にHP回復があるという風に考えればこれも類似性の話にはなる)し、改良ではなくそもそものパーティの発祥(シャフ黒で言えば松山研斗による原型の考案)には共通点や類似性では説明し切れない要素は多々含まれている。とはいえ、シャフ黒の以前にもきりちゃんによる司令塔シャフが、更にそれ以前にも轟雷滅殺剣を採用していない初期型司令塔シャフが存在しており(これらパーティの歴史に関しては下に示す記事を参照)、オリジナルの発案においても過去との類似性が全く無関係という訳でもない。
以上論じてきたように、パーティの考案や改良において、様々な他の事例との共通点、類似性を見ていくことは思考の方法として基本的なものであるということは明らかである。ところが、イルルカSPには903種類にもなる膨大な数のモンスターに加え、スキルや鍛冶のパターン、新生特性をどうするか等、考えなければならない要素は極めて多い。そうなると、プレイヤーは経験に裏打ちされた知識から適切に探索をしているつもりであっても、実際には大量のデータの一部しか検討出来ていないということが起こり得る。配信開始2年が経過しても新しいパーティが未だに考案され続けているのがその証拠であろう。
そして人間には手に負えないような大量のデータをコンピューターを用いて処理し、有益な結果を得る手法を研究する分野として機械学習というものがある。イルルカSPの対戦のような考えるべきことが多い事象において、人間の思考の全部は無理であっても、その一部でも機械に肩代わりして貰うのは有益ではなかろうか(機械学習ではないが、特定の特性を持つモンスターを検索し、個体値や系図によってモンスターのステータスがどのように変化するか計算させたり、機械に使って人間の思考をサポートするのは既にイルルカSPプレイヤーの間で広く行われている)。特に共通点や類似性に基づいた思考は機械学習の一分野である教師無し学習に適している。
機械学習による分析対象の決定
イルルカSPにおいて多々行われる思考は類似性に基づいており、機械学習のうちでも教師無し学習が向いているとは述べたが、機械学習の範囲は広い。またその中で教師無し学習を使うと決めたとしても、ゲームのどの範囲までを分析対象とするか、教師無し学習のうちどの手法を使うか、様々に考えなければならないことがある。分析対象や知りたいことが決まらなければどのような手法が良いかも定まらない為、先ずはイルルカSPのどの範囲を対象とするのか議論する。
ゲームの機械学習による分析と言えば、有名なのはチェスや将棋のAI(artificial intelligence、人工知能)である。これらでは基本的に過去の棋譜と勝敗のデータを集めて分析することで、与えられた盤面においてどちらのプレイヤーがどの程度有利なのか計算する評価関数を構築し、それに基づいてどのような手を場面場面で打てば良いか(より評価関数の値が高い盤面になるか)を計算するという仕組みになっている。より発展したものでは、過去の棋譜を分析するだけでなく、計算機内に評価関数等が異なるプレイヤーを多数作って戦わせ、より強い評価関数を競争や進化のアナロジーから作りだしている。例えば長らく人間有利と考えられていたゲームである囲碁において人間のトップ棋士を破って衝撃を与えたAlphaGoは後者のメカニズムに基づいている。
これと同じように考えれば、コンピューター内に多数のパーティを生成し、それら同士で対戦させ、どのような作戦と命令をどのような状況に対し与えたか、その結果勝敗がどうなったか記録し、それに基づいてパーティとその運用方法を改良していけば、人間の手に依らずとも自動で最強のパーティとその動かし方が分かることになる。実際、育成対戦ゲームという点ではDQMと似ているポケモンに関しては、対戦AIを構築している人がいる。
http://julian.togelius.com/Lee2017Showdown.pdf
では、これと同じことがイルルカSPでは可能なのか。無理。その理由はDQMの対戦がAI(これはDQM用語のAIであり人工知能一般のことではない)に強く依存し、お互いのプレイヤーの入力が与えられても次のターンの状態を正確に記述出来ないからである。
ポケモンの場合、お互いのプレイヤーが命令を下すと、素早さが1でも高い方が必ず先に動き、命令された技1つだけを使う。そしてその技が与えるダメージも、乱数や急所等の要素はあるが、確率p%で相手の残りHPはhになるという遷移が正確に書ける。後攻側のポケモンの行動による先攻側のポケモンの残りHPが幾つになるか、その遷移確率も正確に書けるのは変わらない。技の追加効果で状態異常が発生したり、攻撃技だけでなく変化技もあったり、ポケモン交代という行動を考慮したとしても、次のターンの状態としてどのような状態があり得るか、その状態に到達する確率は何%か、それは完全に正しく計算することが出来るのである。確率要素こそあれ、チェスや将棋、囲碁とこの点では本質的に変わらない。
しかしイルルカSP(に限らずDQM)は、その対戦においてAIというシステムが大きな意味を持っている。例えばAI2回行動のモンスターは1ターンに2回連続で行動する訳であるが、1回目の行動こそ何の技を使うかプレイヤーは正確に指示出来るものの、2回目の行動で何を行うかはAI任せで、何をするか予想することが出来ない。作戦がガンガンいこうぜなら攻撃技を使い易い、命大事にならば回復技を使い易いという傾向こそあるものの、AIがどのように作られているか公開されていない為、どの作戦ならどの技を何%で使うのか、正確な確率分布は不明である。そうであるが故に、コンピューター内でDQMの対戦は正しく模擬することが出来ず、コンピューター内に作った多数の仮想的なプレイヤー間の競争とパーティ・戦略の進化による最強パーティ構築は不可能なのである。
それに対し、コンピューター内でDQMのAIが模擬出来ないなら、コンピューター内に対戦環境を構築せず、スマートフォンやゲーム機を操作させるロボットにしてしまえば良いという反論を思い付く人がいるかもしれない。腕や指のあるロボットを開発し、スマートフォンを操作してイルルカSPの対戦を只管やらせ続け、最強パーティを作らせると。しかしながら、このアイデアには致命的な欠点がある。スマートフォンを操作出来る器用な手先、カメラで写したゲーム画面の画像からゲームの状況を理解する画像処理、これらの技術開発のコストが極めて大きいということのみならず、これらの問題を仮に解決出来たとしても、絶対に問題として残る致命的な欠点が。それは折角機械を使っているのに、現実のスマートフォンやゲーム機を操作させていたのでは、人間と同じ、或いはそれより遅い速度でしか経験が積めないということである。コンピューター内で計算が完結するからこそ、ゲームの対戦で人間が1試合に5分かそれ以上かかる間にコンピューターは1秒で何千何万回と試合出来るから人間より強くなれるのに、スマートフォンやゲーム機を操作していては人間と同じ試合数しか行えない。ロボットを大量生産して一斉にゲームをやらせ、学習結果を適宜共有するのであればロボットの台数倍の学習量にはなるが、それでもコンピューター内で計算が完結するのに比べたらゴミのような学習量に過ぎない。如何に優れた機械学習手法であれ、1つの物事から学べる内容は人間と比べて圧倒的に少なく、処理するデータ量の膨大さに頼ることで漸く人間に勝つのがAIであるから、この方法は駄目なのである。
以上により、機械学習を用いても人間の手を介さずに自動で最強パーティ、最強戦略はイルルカSPの場合には構築出来ないということが分かった。従って、機械学習をイルルカSPに適用する場合、全自動でパーティ構築をするのではなく、人間がパーティ構築を思い付く手助けを行うという形式になる。前項で人間がどのような思考に基づいてパーティ構築を行っているのかわざわざ詳細に分析したのは、これを見越してのことである。機械学習に全てを任せるのではなく、ぼんようの作ったモンスターやスキルの検索、耐性シミュレーション機能や、小梢祐治の個体値・系図によるステータス計算ツール等と同じように、人間のサポートが目的となる。ではそれら既存のものとの違いはと言うと、大量のデータを分析することで、最初からは見えていないデータ間の相関関係を明らかに出来るという点である。即ち、ここで用いる機械学習とは「すごい統計分析」というイメージになる。
対戦のシミュレートを伴う分析は不可能だということはこれまで述べてきた通りなので、対戦を介さないで調べられる範囲、例えば、モンスターのステータスや特性、耐性といったデータだけを見て、「スモボ化マジェス・ドレアムとAI3新生ティコはどちらもAI3回行動で常にアタックカンタを持つスモールボディのモンスターなので似ている」というような、モンスター間の類似性の検出ということになる。このような類似性の検出が出来るだけでも、既存のパーティにおける各モンスターの採用基準を理解するのに役立つであろうし、使用モンスターに制限のかかる対戦会において、自由にモンスター選択の行えた段位戦での構築に最も近いのはどのような構築か考える上での一助となるであろう。
機械学習の参考書例
原著は2006年と昔から出版されていて、定評があるのが『パターン認識と機械学習』、通称PRML(pattern recognition and machine learning)である。機械学習の分野では5年も経てば古い本とされている中、2022年現在でも東大本郷キャンパスの生協書籍部に平積みにされている程である。しかしながら当然古いので、今流行りの深層学習(deep learning, DL)については書かれていない。それでも機械学習全般について大まかに知り、インターネットで最新の状況を知る前の基礎固めには良いのではないか。機械学習の理論の数学的解説は詳しめ。但し下巻の訳者あとがきに”統計よりであるため,人工知能で扱う概念学習,クラスタリングや強化学習,一階述語論理に基礎を置く帰納論理プログラミング,極限における同定などの計算論的学習理論などのいくつかの手法がカバーされてない”と書かれている等、名著ではあってもこれ一冊で万事対応可能という訳ではない。
コンピューター、情報科学関係の本の出版で有名なオライリー社から出ている新しめの機械学習の教科書。機械学習のアルゴリズムだけでなく、よく使われるライブラリやDLにおいて重要な学習済みデータの入手法まで記載されているので、PRMLと比べると理論というより実践向き。しかしながら、各機械学習手法の数学的性質とそこから導かれる欠点や注意点についても簡潔に述べられているので、これだけ読んでも十分に使える。
モンスター間の類似性計算の方法の検討
前処理の重要性
先ず、イルルカSPに登場するモンスターのデータがどのような情報を含んでいるか確認する。例えばマジェス・ドレアムを具体例として挙げると下表のようになる。

このように、ステータス上限値、特性、耐性合わせると46項目も存在する。そしてステータス上限のように数値で表されたデータ(量的データ)もあれば文字で表され、決まった種類の何れかで表されるようなデータ(質的データ)も系統や特性として存在する。各属性への耐性は弱点、普通、軽減、半減、激減、無効、吸収、反射の8種類のうち1つだけを取り得るという点を見れば質的データではあるが、攻撃技で受けるダメージや補助技へのかかり易さを段階的に表現したものなので、例えば-1,0,1,2,3,4,5,6という風に数字に変換し、量的データとして取り扱う方が適切に思える。ここで耐性を数字に変換して量的データとして扱うことの妥当性を理解するには、量的データとして扱ってはいけないものを量的データに変換してどのような不都合が出るか考えてみれば良い。例えば系統(スライム、ドラゴン、自然、魔獣、物質、悪魔、ゾンビ、???の8つの値を取る)を0,1,2,3,4,5,6,7に変換し、数値間の距離を考えてみれば良い。本来8つの系統はそれぞれ異なり、どれとどれが似ていてどれとどれは特に差が大きいという区別の無いものだが、このように量的データとして扱ってしまうと、魔獣(=3)と物質(=4)は差が1しかないから似ている、スライム(=0)と???(=7)は差が7もあるから違いが大きいとなり、不自然なこととなる。質的データをどう入力し、どう扱うかはここではまだ述べずに後に回す。逆に耐性に関しては、弱点と普通は似ている、半減と激減は似ている、弱点と反射は違いが大きいという関係を表現したいので、質的データではなく量的データとして扱うべきである。
さて、46項目のデータを持つモンスターが全部で903(モントナーの性格違いを含めれば908)種類存在する訳であるが、当然、このような膨大なデータを人間が眺めていてすぐに役立つ情報なりデータ間の関係性なりを発見出来る筈もないし、コンピューターと雖もいきなり渡されて適切な分析が出来るということもない。そこで、コンピューターが分析出来、そしてその分析結果が人間にとって有益なものとなるよう、データの形式を整理しなければならない。これら一連の処理を前処理と呼ぶ。耐性が文字で表現されていたのを数値に変換し、量的データとするのもその一つである。
前処理の重要性を理解する為、何も前処理をせずいきなりデータをグラフに描いてみる。各モンスターを点として、1つの点が46項目の値を持っているので46次元空間に散布図を描けます……描けない。人間が理解し、またコンピューターのスクリーンに表示出来る画像は2次元か3次元が限界なので、46次元空間に点をプロット出来ることに意味は無いからである。散布図を映すカメラの角度を考える必要が無く、かつ1次元よりは情報量が多い2次元でのプロットをしてみることとする。滅茶苦茶雑であるが、殆どの項目を消してHPとMPのみ残して平面上にプロット。すると下図が得られる。

この散布図を見て「HPが3500とトップ、MPも800程度となかなか良いモンスターがいるぞ、彼こそ最強だ」と考えた人はいるだろうか。イルルカSPで対戦、それ以前に育成だけでもしていたならばそう考えなかった筈である。というのも、先に答えを言うと、この最強モンスター(仮)の正体は

_人人人人人人人_
> ギガハンド <
 ̄Y^Y^Y^Y^Y^Y ̄
だからである。イルルカSPプレイヤーならもうこれだけで分かるであろうが、そうでない読者を想定し、イルルカSPの基本的な仕様と、それが原因で発生するモンスターのステータスの見かけ上の大差について説明する。
イルルカSPでは、戦闘に使うモンスターは表と裏、それぞれ合計4枠までのモンスターで構成する。「匹」ではなく「枠」なのがポイント。即ち、身体が小さいか普通のモンスターは1枠、やや大きめのモンスターが2枠、巨大なモンスターが3枠、超巨大モンスターが4枠という差異がある。即ち、一度に戦闘に参加する自分のモンスターの数は一定ではなく
1枠+1枠+1枠+1枠 (4匹)
1枠+2枠+1枠 (3匹)
2枠+2枠 (2匹)
1枠+3枠 (2匹)
4枠 (1匹)
という5パターンが存在する。当然、大きなモンスター程戦闘に参加出来る匹数が減る為、サイズが大きくなるとステータスが高くなる。ギガハンドは3枠モンスターであり、その分だけステータスが高くなっている。
またDQMではモンスターの1ターンにおける行動回数は一定ではない。あるモンスターは1回しか動かないが、別のモンスターは3回動く等の違いが存在している。複数回行動し得るモンスターはAI〇回行動という特性を持つ。当然だが、単に行動回数が異なるだけであると強さに大きな不公平を生じる。そこで、AI〇回行動の特性を得ると、行動回数の多さに応じてステータスが低下する。ギガハンドは1回行動であり、行動回数によるステータス低下を受けていない。
イルルカSPでは新生配合によってモンスターのサイズや行動回数は(ある程度の制限はあるが)変えられるようになっていて、特性による補正を受ける前の各モンスターの素のステータスの合計値は全モンスターがほぼ同じ値になるように調整されている。即ち、ギガハンドが最強(仮)であったのは、3枠以上で1回行動のモンスターが彼だけであったことのみに由来する表面的なものであり、本質的な意味を持っていないということである。逆に、イルルカSPに関して詳しくない人であれば、ここまで説明を受けるまでは散布図を見てギガハンドを素直に最強だと思っていた筈である。このことは、前処理が適切に行われているかどうか判断するには、分析対象についての知識(ドメイン知識)が必要であるということを意味している。兎も角、サイズや行動回数によるステータスの補正は分析の前に取り除いておくべきであろう(DQMJ3PのようなDQMの他作品とは異なり、実際には単に特性による補正を全て消せば良いという単純な問題ではないことは、イルルカSP固有の他のドメイン知識共々後述する)。
そして、分析対象に依存しない前処理として、データの各項目間での数値のスケールの調整がある。例えば今回の場合、ステータスの数値は数百から数千の範囲を、耐性の数値は一桁の数字になる訳だが、このまま単純に2つのモンスターとモンスターの間の距離を計算すると、数値のスケールが大きいステータスの影響ばかりが出てしまい、耐性が分析結果にほぼ反映されなくなってしまう。その為、項目毎にその値の平均と標準偏差を計算し、規格化と呼ばれるものを行わなければならない。分かり易い例として、年齢と年収を散布図にプロットするということを考える。データは以下の架空のものを用いる(年齢を20~60、年収を100万~2000万の範囲でランダムに生成)。

このデータを何も考えずそのままExcelで散布図にすると次のようになる。

これを見て「数値の値は滅茶苦茶違うけど奇麗に図が描けている」と思ってはいけない。x軸とy軸をよく見てみよう。縮尺が全然違います。つまり、このグラフは本当は「ゴンさん」の髪の如く、縦に異様に長くて横にはとても狭い形をしている。

このような「ゴンさんの長い髪」の中にデータが分布しているとするならば、2点間の距離は殆ど縦方向の差で決まり、横方向はほぼ関係ないことは明らかであろう。年齢と年収のグラフは本来はそうなっている。にも関わらず、Excelの描いた図が人間の目にまともに見えるのは、横と縦で縮尺を変えているからである。この「縮尺を変える」に相当する前処理が、数値から平均を引いてデータの平均を0にし、その上で標準偏差で割って数値のばらつきの大きさを統一するという、規格化という処理に当たる。これをしないと、20歳年収700万円と50歳年収900万円の2人の違いは年齢より年収だという間違った結論が導かれてしまう(200万>>30だが、年収200万の差より年齢30の差の方が明らかに重大だ)し、イルルカSPではモンスターのステータスを見て耐性は無視するという、凡そプレイヤーにとってほぼ意味の無い分析をしてしまう。
機械学習の重要性
ギガハンドの存在によって前処理もせずにHPとMPでプロットするのは問題があるというのは明らかになったが、前処理をしただけでは有益な散布図にならないであろう。特性によるステータス補正を消せばギガハンドが最強に見える状態は解消するが、それだけだからである。高次元データはそのままでは意味不明なので機械学習による分析を経ることで有意義な結果を得たい訳だが、その為に必要な機械学習手法としてどういうものがあるか、簡単に見ておく。
次元削減
第一に、HPとMPしか見ていないので必要な情報が欠落している。以前対戦で強いモンスターを探せる条件として「状態異常耐性の高いスモールボディのモンスター」というものがあるというのは既に述べた通りである。ここではステータスではなく耐性や特性を見ているが、その情報はこの散布図には全く含まれていない。かといって、必要になった項目2つだけを取り出して同じような散布図を描けば良いというものでは当然ない。そうであれば探索条件が3つ以上になった時に対処出来ないし、どのような項目2つの組か事前に分からなければ、46項目から2つの項目を選ぶパターン、即ち$${_{46}\rm{C}_{2}=1035}$$個の散布図を見て人間が意味を汲み取らないといけないが、これは明らかに不可能である。つまり何らかの方法によって、46次元もの情報を2次元、多くても3次元に縮約しなければならない。46次元の情報を2次元に落とせば当然欠落は起こるのだが、どうやって重要な情報は残るようにするか、それが機械学習によって解くことを期待される問題である。
第二に、これは第一の点とも関係するのであるが、散布図における点の並びが人間に解釈出来るものとなっていない。HPが異様に低い幾つかの点はメタル系スライム、逆にHPが異様に高い点はギガハンドのような巨大モンスターを表しているのだろうということは分かるが、殆どの点が1つの塊の範囲内に押し込められていて、見ていて何も分からないものとなっている。しかし機械学習に明るくない者にとっては、見て意味が分かる図が存在するということの方が不思議に思えるであろう。見て意味が分かる図としては、下図のようにデータがx,y軸それぞれで上手くばらついているのが良い。
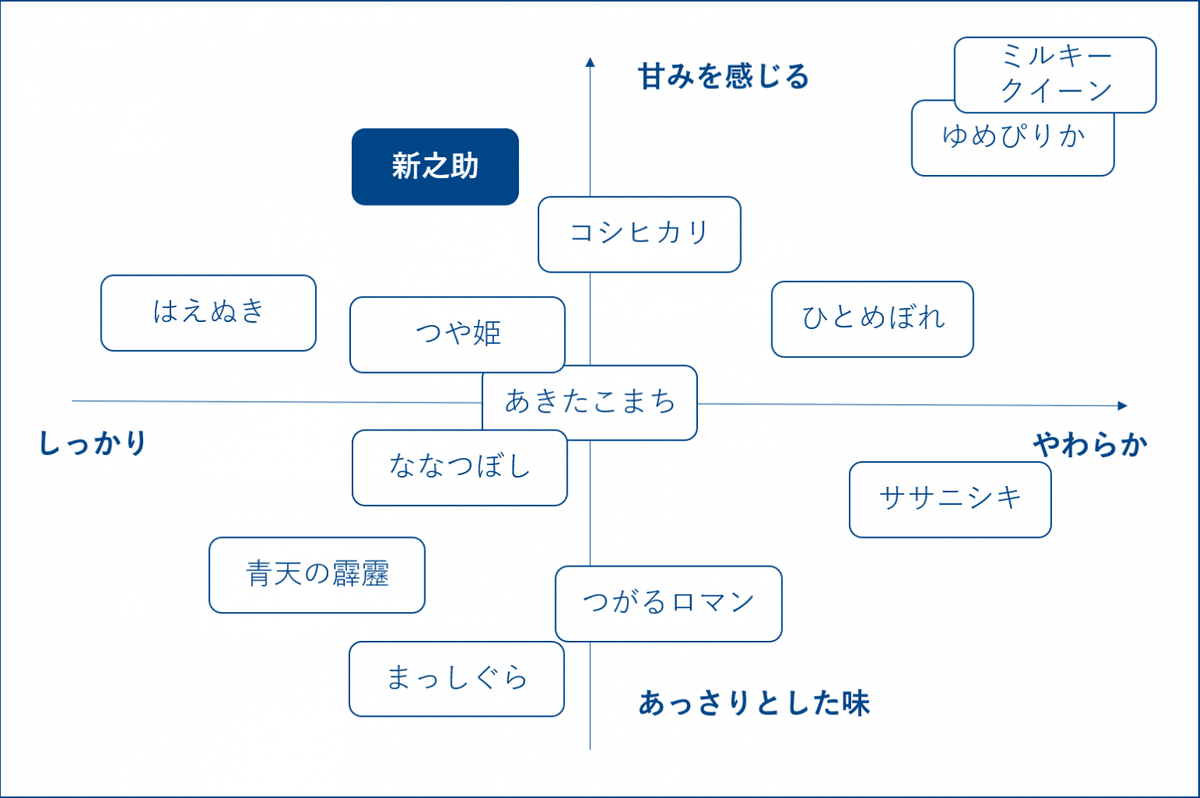
機械学習によって2次元に次元削減した場合に、上に示したポジショニングマップのように横軸や縦軸が人間にとって意味の分かり易い軸になっている可能性は低い(46次元分の情報を複雑に混ぜ合わせているのだから寧ろごちゃごちゃだろう)のだが、軸の成分を調べれば何か解釈出来る可能性はあるかもしれない。機械学習では一ヶ所に固まらず、平面上に出来る限り広がるように理論や技術が進展している筈なので、様々な次元削減手法を試し、データの分布の仕方と相性が良くて有意義そうであったものを最終的に分析結果として採用すれば良い。そしてデータが一ヶ所に固まらず広く散布しているということは、モンスター間の違いを表す特徴を上手く抽出出来ているということを意味している。大量のモンスターのうち対戦で使われるものは極一部なので、強いモンスターの特徴というのは何らかの意味で顕著、他のモンスターから区別され易いだろうと考えると、モンスター間の違いを上手く抽出出来ていれば強いモンスターの位置というのも自然と表れてくるような気がする(これは本当に根拠無し)。この意味で、第一の点とも関係してくるのではないかと予想している(少なくとも今のような一ヶ所に固まった分布からは何も言えないのは確かである)。
これら次元削減の内容は『scikit-learn、Keras、TensorFlowによる実践機械学習 第2版』の第8章、次元削減に相当する。ここまで次元削減がきちんと行えるかのように書いてきたが、次元を減らしても情報量の欠落が意外と小さいという仮定に疑問を持っている人は多い筈である。この疑問に対する回答も実はその本の同章に書かれている。それが多様体仮説である。
データは空間上に均一に分布している訳ではなく、特徴量(項目)間に相関があり、それ故より低次元の構造の上に集中しているという考え方である。例えばイルルカSPの場合、モンスターの持つ耐性は30項目もあり、よく対戦に使われているモンスターであっても多くのプレイヤーは各項目の内容をきちんと把握することは本来困難である。世の中を見ればポケモンのタイプ相性$18*18=324$パターンすら満足に覚えられない人がいるのに、イルルカSPのモンスターの耐性$${903\times30=27090}$$パターンを覚えるのは尚更困難であろう。しかし現実には大雑把にではあるが、対戦にあまり使われないモンスター含めて耐性が把握されている。というのも、系統毎に耐性には一定の共通点があり、それを覚えておけば大抵のモンスターの耐性を細かく覚える必要は無いからである。即ち、モンスターの耐性は30項目にも及ぶ膨大なデータに見えて、その大部分は系統という8種類の値しか取らない1つの質的データで説明が付くのである。尤も、当然ながら、系統共通の耐性に従わない部分を持つモンスターは多い。それでも、耐性が全て無秩序に決まっている場合よりは情報量は少なく、分布に偏りがあることは間違いない。そうであるから、本来30次元で表現されなければならない情報が、より少ない次元でほぼ表現出来るであろうと考えられるのである。このような状況は、視覚的には3次元空間内に散らばる点が、実は何らかの平面、或いはねじられたり回転したりした曲面上にばかり乗っているようなものである。上手く空間に変換を加えることで、3次元の分布を2次元の分布にすることが出来る。空間内に自由にデータが分布するのではなく、その一部に過ぎない多様体上に基本的には分布しているだろうという仮説なので、これは多様体仮説と呼ばれる。
この多様体仮説、イルルカSPのようなゲーム、即ち人間が意図的に設計したものにおいては妥当そうに見えるが、それ以外のもの、意図的に法則を組み込まれた訳ではないものに対しては成り立つのであろうか。これに関する私の考えを書くと、機械学習の分析対象にしようと思った時点で、多様体仮説をデータが満たすことを前提としている、言い換えると、多様体仮説に従わないデータは分析する価値が無いと思っている。というのも、多様体仮説に従わないデータの典型例の一つは、作図の為だけに作った年齢と年収の架空データのように、前項目を範囲内でランダムに生成したものである。このようにすればデータの数が増やせば空間内を均一に埋め尽くすが、何の法則性も無い為、機械学習によって法則性を見出す意味も無い。この推論はあくまで全項目がランダムという非現実的なデータに関して考察したのみであり、多様体仮説に従わない任意のデータに対して機械学習の有用性を否定した訳ではないが、直感的にはこういうことだろうと思っている。
次元削減によく使われる手法としてはPCA(principal component analysis: 主成分分析)、カーネルPCA、LLE(locally linear embedding: 局所線形埋め込み法)、ランダム射影(random projection)、多次元尺度法(multidimensional scaling: MDS)、Isomap、t-SNE(t-distributed stochastic neighbor embedding: t-分布型確率的近傍埋め込み法)、線形判別分析(linear discriminant analysis: LDA)等がある。各手法の詳細は実際にデータをその手法で分析する段階に回す。
クラスタリング
次元削減の項では、次元削減によってデータを2次元(或いは3次元)まで落とし散布図として可視化することで、近い点と点、即ちモンスター同士は似ているということを人間の目によって判別するということを考えていた。しかしながら、46次元もの情報を2次元に落とし込んで機能すると考えるのは当然無理がある。そこで、高次元のまま、人間の目を介さずモンスターを類似性の高いもの同士を結び付け、グループ分けされた結果だけを得たいという発想が生じてくる。それがクラスタリングである。
クラスタリングの手法として有名なのがk-means法で、改良形としてaccelerated k-means法、ミニバッチk-means法がある。その他の手法にはDBSCAN、凝集クラスタリング(agglomerative clustering)、BIRCH(balanced iterative reducing and clustering using hierarchies)、平均値シフト法(mean-shift)、アフィニティ伝播法(affinity propagation)、スペクトラルクラスタリング(spectral clustering)等がある。この辺は『scikit-learn、Keras、TensorFlowによる実践機械学習 第2版』の第9章を参照。
但し、クラスタリングがあるから前項で述べてきた次元削減が無意味になるという訳ではない。というのも、高次元データに対する機械学習は単に計算時間がかかるというだけでなく、出す解が不正確になりがちだからである。
よく言われるのが次元の呪いとそれによる過学習である。即ち、次元が高くなると空間(データの取り得る範囲)におけるデータの密度が低くなり、予測が不正確になるということである。例えば、1匹の猫だけを見て「猫は白黒の体毛に覆われた生き物だ」と考えるのは間違っている。1匹の猫から本来学習すべきでないことまで余分に学習してしまっている。こういうのを過学習と言う。そして、1匹の猫だけを見て「動物は白黒の体毛に覆われた生き物だ」と考えたり、「世界は白黒の体毛で出来ている」と考えたならば、もっと間違いは酷くなっている。データの取り得る範囲、即ち次元が広がったにも関わらず、観察したデータの量は増えていないからである。これは過学習が悪化した例であるが、次元が増えれば低次元では正しい結論を出せていたデータ量であっても間違った結論に至るということはあり得る。例えば100匹の猫を見て猫の特徴を学ぶことは出来るが、そこから動物や世界の特徴を予想したなら間違う。100種類の動物をそれぞれ1匹見て動物の特徴を予想するというのも、例えば猫に関しては1匹しか見ていないのだから、猫の体毛は白黒に違いないと決めつけて間違ったりする。次元が増えれば計算量だけでなく必要なデータ量が飛躍的に増える、これが次元の呪いである。
加えて、高次元に存在する多様体上に散布するデータは低次元に移し替えた方が分かり易く、機械学習にも適していることが多い。下の写真に描かれている絵は3次元空間に存在する2次元多様体である。

当然、このままだとよく分からないが、平面に移せば分かり易くなる。

データセットによっては次元削減した結果却って複雑になることもない訳ではないが、次元削減のメリットは計算時間の削減や過学習抑制だけでなく、得られる解の改善にも役立ち得るということは重要である。
続きについて
ここまででかなり長くなってしまったので、イルルカSPのモンスターデータの前処理の具体的な難所やその対処方法の検討、機械学習の実践については、次回以降の記事に回します。
著作権者表記
このページで利用している株式会社スクウェア・エニックスを代表とする共同著作者が権利を所有する画像・動画の転載・配布は禁止いたします。
また動画で用いられたスギヤマ工房有限会社が権利を所有する楽曲の転載・配布は禁止いたします。
