
論文を読む Bui Tuong Phong(1975) Illumination of Computer-Generated Images
Illumination of Computer-Generated ImagesはBui Tuong Phongによって1975年に発表された論文です。現在Phongシェーディングとして親しまれている手法はこの論文がベースになっているそうです。
論文はこちらからダウンロードできます。
論文について
イントロ部分では70年代のコンピュータによるレンダリング技術の発展についてふれ、2つの大きな問題があったそうです。
1. hidden faceをレンダリング時、いかに除去するか
2. シェーディング技術どうしていくかという問題
この論文では2について、大きな課題として3つ上げています。
1. リアルタイムにレンダリングできる(30FPS)。
2. スームズな表面としてレンダリングする
3. デジタルサンプリングの影響を除去する(原文ではelimination or attenuation of the effects of digital sampling techniquesとあり、うまく訳せなかったですが、、)
(p311のIntroductionより)
前半部分ではhidden faceについて触れています。現在WebGLだと
gl.enable(gl.DEPTH_TEST);とdraw関数の前に宣言することでレンダリングの際に自動的にdepth bufferを比較し、hidden surfaceの除去を行ないます。
既存のシェーディングの問題として、当時は頂点での法線ベクトルと光線方向のベクトルを利用する'cosine law'でシェーディングの値Spを以下のように求める方程式をベースにする手法が主流だったそうです。
![]()
Cpは反射係数、iが光線と法線ベクトルの角度で内積cos(i)は求めることができます。
論文の中で既存のシェーディング技術としてWarnock's shading, Newell, Newell, Sancha's shading, Gouraud's shadingの3つ上げています。Gouraud's shadingの手法では局面でのシェーディングを開発しています。陰影の濃淡を頂点上で計算し、線形補間を行って面上での色の計算を行っています。この手法だとリアルに近いレンダリングに近づきますが、ポリゴンの境界での非連続性をどうするか問題があります。
ポリゴンの境界で法線ベクトルの値が非連続に変化し、反射の値が非連続に変化します。非連続に変化する色の変化面はよりはっきり見えるそうです。その効果はMach Bandsと言うそうです。
ポリゴンのを大きさを小さくしていき、ポリゴンの数を多くしていってもMach bandsは避けられません。
そこでBui Tuong Phong氏(以下Phong氏)による手法が提案されています。各頂点での法線ベクトルを面のあらゆる点で計算していくことでよりスムーズなレンダリングを実行していこうとするものです。
GLでいうとvertexシェーダーで法線ベクトルなどを利用して反射・拡散を計算するのではなく、fragmanetシェーダーに法線ベクトルをvarying variableとして渡して、fragmanetシェーダー上での反射・拡散を計算し、レンダリングを行う感じでしょうか。
シェーディングモデルの方程式は論文の中で以下のように紹介されています。

方程式でCpはポイントpでの反射係数でW(i)は鏡面反射率を表しています。
iはポイントpでの入射角、dは環境拡散反射係数、sは反射角とカメラの方向ベクトルとの角度、nは輝度として定義されています。
この論文で紹介した手法、現在さPhong shadingという手法として知られています。
拡散反射(diffuse reflection)
方程式の右辺の左部分は拡散反射(diffuse reflection)を表しています。
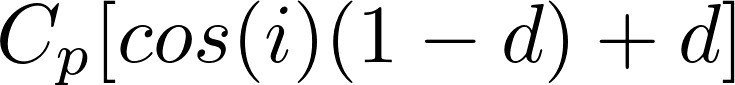
拡散反射で必要な角度iを簡略に図式化すると以下のようになります。

入射角iは光源からの方向ベクトルlと法線ベクトルnとして内積として求められます。ここでd=0として以下のように書き換えます。

拡散反射をwebglで実装してみました。光は論文と同じようにdirectional lightとして光の方向はguiから変更できますが、デフォルトの値は3Dモデルの正面からの光を照らすようになっています。
拡散反射の値は法線ベクトルと光源からの方向ベクトルで決定されるので、カメラの位置に関係なく値は変化しません。
鏡面ハイライト( specular highlight )
方程式の右辺の左部分は拡散反射(diffuse reflection)を表しています。

鏡面ハイライトで必要な角度sを図式化すると以下のようになります。

反射ベクトルrは法線ベクトルnに対して光源から方向ベクトルlと対称なので以下のように示すことができます。

鏡面ハイライト(specular highlight)はカメラ方向へのベクトルvと反射ベクトルrの内積として角度sを求めることができるので、以下のように書き換えることができます。

鏡面ハイライトをwebglで実装してみました。拡散反射と同じようにしています。
3Dモデル上の点からカメラへの方向ベクトルがカメラの位置・向きによって変化するので、拡散反射と違い色が変化するのがわかります。
Phong shading
拡散反射と鏡面ハイライトの和として以下のようにphong shadingは実装できます。

p.317のConclusionにあるように、Phong shadingはポリゴンとポリゴンとの境界での値の変化がGouraud smooth shading modelに比べて顕著ではなく、計算もそこまで大きくないと言っています。それでも単位ベクトルを求めるなど、計算量はやはりGouraud smooth shading modelに比べてやや大きいものになっています。
有名な論文をメインに読みながら、まとめ、実装してみるということを試験的にやっていきました。Bui Tuong Phong(1975) Illumination of Computer-Generated Imagesを取り上げました。
まとめて実装していくのは思った以上に時間がかかりますが、その当時の置かれている状況など論文から読み取れることは非常に素晴らしいです。時間を見つけながら、やっていきたいです。


