
小角X線散乱(SAXS)(12) - 【演習】高分子のガウス鎖の散乱関数
高分子のガウス鎖の散乱関数(形状因子、干渉因子)を求める問題です。
【演習】高分子のガウス鎖の散乱関数
図1のように、ランダムに配向しているガウス鎖(高分子のモデル)がある。$${1}$$から$${N}$$まで$${N}$$個のセグメントが連なっているとし、各セグメントには$${f}$$個の電子があるとする。

ガウス鎖の定義:
$${n}$$個離れたセグメントが$${\boldsymbol{r}}$$から$${\boldsymbol{r}+\mathrm{d}\boldsymbol{r}}$$だけ離れる確率を$${W(\boldsymbol{r})\mathrm{d}\boldsymbol{r}}$$とする。確率密度$${W(\boldsymbol{r})}$$が次式のように、距離$${r}$$の関数として与えられる高分子鎖をガウス鎖と呼ぶ:
$$
W(r) = \Big (\dfrac{3}{2\pi nl^2} \Big )^\frac{3}{2} \exp \Big ( - \dfrac{3r^2} {2nl^2} \Big ) \;\;\;\;\;\;\;\;\;\; (1)
$$
ここで、$${l}$$はセグメント間の長さ(ボンド長とも)。ちなみに、
$$
\displaystyle \int_0^\infty W(r) \mathrm{d}\boldsymbol{r} = 1 \;\;\;\;\;\;\;\;\;\; (2)
$$
ガウス鎖は長いミミズみたいに絶えず形を変えています。
(問1) 全電子数$${N_e}$$を求めよ。
(問2) 式(2)を証明せよ。
(問3) 散乱強度$${I(h)}$$を求めよ[1]。ただし、$${h}$$は散乱ベクトル$${\boldsymbol{h}}$$の大きさである[1]。
(問4) 散乱関数$${P(h)}$$を求めよ[1]。
(問5) 回転半径$${R_G}$$を求めよ[1]。
1) 用語の定義については、文献[1]を参考にしてください。
【解説】
(問1) $${N}$$個のセグメントに同じように$${f}$$個の電子があるから、
$$
N_e = Nf
$$
(問2) 積分の領域$${V}$$を無限大とし、極座標系で考える。極座標系では、体積要素$${\mathrm{d}\boldsymbol{r}}$$は、$${r^2 \sin\theta \mathrm{d}r \mathrm{d}\theta \mathrm{d}\varphi}$$となるから[2]、式(2)の左辺は次のように変形されます:
$$
\displaystyle \int_V W(r) \mathrm{d}\boldsymbol{r} = \int_{r=0}^\infty \int_{\theta=0}^\pi \int_{\varphi=0}^{2\pi} \Big (\dfrac{3}{2\pi nl^2} \Big )^\frac{3}{2} \exp \Big ( - \dfrac{3r^2} {2nl^2} \Big ) r^2\sin\theta \mathrm{d}r \mathrm{d}\theta \mathrm{d}\varphi
$$
$${\theta}$$と$${\varphi}$$の積分は先に実行できて、答は$${4\pi}$$になります[3]。その結果、
$$
\displaystyle \int_V W(r) \mathrm{d}\boldsymbol{r} = 4\pi \Big (\dfrac{a}{\pi} \Big )^\frac{3}{2} \int_0^\infty e^{- ar^2} r^2\mathrm{d}r
$$
ここで、見やすくするため、
$$
a = \dfrac{3}{2nl^2} \;\;\;\;\;\;\;\;\;\; (3)
$$
とおきました。
ここで数学公式から[4]、
$$
\displaystyle \int_V W(r) \mathrm{d}\boldsymbol{r} = 4\pi \Big (\dfrac{a}{\pi} \Big )^\frac{3}{2} \times \dfrac{\sqrt \pi}{4} a^{-\frac{3}{2}} = 1
$$
(証明終)
(問3) ガウス鎖は球や円柱のように連続体でないので、構造因子$${F(\boldsymbol{h})}$$を計算するのではなく、散乱強度$${I(\boldsymbol{h})}$$の離散点の式を使います[1]:
$$
I(\boldsymbol{h})=A_e^2\displaystyle\sum_{j}\displaystyle\sum_{k}f_jf_k e^{-i\boldsymbol{h} \cdot (\boldsymbol{r}_k-\boldsymbol{r}_j)}
$$
各セグメントの電子数は同じなので、$${f_j = f_k = f}$$:
$$
I(\boldsymbol{h})=A_e^2 f^2 \displaystyle\sum_{j=1}^N\displaystyle\sum_{k=1}^N e^{-i\boldsymbol{h} \cdot \boldsymbol{r}_{jk}} \;\;\;\;\;\;\;\;\;\; (4)
$$
ここで、$${\boldsymbol{r}_{jk} = \boldsymbol{r}_k - \boldsymbol{r}_j}$$は、散乱点$${j}$$から散乱点$${k}$$に向かうベクトルです。
ガウス鎖は形を変えランダムに配向するので、散乱ベクトル$${\boldsymbol{h}}$$を$${z}$$軸においておきます(図2)。
図2のように極座標系で考えます。まず、$${\boldsymbol{r}_{jk}}$$はランダムにあらゆる方角に向くので、観測される散乱強度は方角についての平均となります。さらに、セグメント$${j}$$と$${k}$$間の距離$${r_{jk}}$$も確率密度$${W(r)}$$に従うので、散乱強度はそういう意味でも平均となります。なお、本来は平均を表す$${\langle I(h) \rangle}$$と書くべきですが、慣例に従って、そのまま$${I(h)}$$と書きます。

$${\langle \cdots\rangle}$$を方角と距離の平均をとるという意味で使うと、
$$
\langle e^{-i\boldsymbol{h} \cdot \boldsymbol{r}_{jk}} \rangle =\displaystyle \int_{r_{jk}=0}^\infty \int_{\theta=0}^\pi \int_{\varphi=0}^{2\pi} W(r_{jk}) e^{-ihr_{jk}\cos\theta} r_{jk}^2 \sin\theta \mathrm{d}r_{jk}\mathrm{d}\theta\mathrm{d}\varphi = \\ =2\pi \int_0^\infty W(r_{jk})\Big [ \int_0^\pi e^{-ihr_{jk}\cos\theta}\sin\theta \mathrm{d}\theta \Big ] r_{jk}^2 \mathrm{d}r_{jk}
$$
ここでは、ベクトルのなす角が$${\theta}$$なので、内積$${\boldsymbol{h} \cdot \boldsymbol{r}_{jk} = hr_{jk} \cos\theta}$$となります。$${\theta}$$に関する$${[\cdots]}$$の積分を実行します。その前に、積分変数の変換をします。$${x = \cos\theta}$$とすると、$${\mathrm{d}x = - \sin\theta \mathrm{d}\theta}$$だから、
$$
\displaystyle \int_0^\pi e^{-ihr_{jk}\cos\theta}\sin\theta \mathrm{d}\theta = \int_1^{-1} e^{-ihr_{jk}x} (-\mathrm{d}x) = \int_{-1}^1 e^{-ihr_{jk}x}\mathrm{d}x = \\ = \Bigg [ \dfrac{e^{-ihr_{jk}x}}{-ihr_{jk}} \Bigg ]_{-1}^1 = \dfrac{e^{-ihr_{jk}}-e^{ihr_{jk}}}{-ihr_{jk}} = \dfrac{e^{ihr_{jk}}-e^{-ihr_{jk}}}{ihr_{jk}} =\dfrac{2\sin{hr_{jk}}}{hr_{jk}}
$$
ここで、正弦関数の複素数表現、
$$
\sin z = \dfrac{e^{iz} - e^{-iz}}{2i}
$$
を用いました。こうして、積分変数$${r_{jk}}$$だけの積分が残ります:
$$
\langle e^{-i\boldsymbol{h} \cdot \boldsymbol{r}_{jk}} \rangle = \\ = 4\pi\displaystyle \int_0^\infty W(r_{jk}) \dfrac{\sin{hr_{jk}}}{hr_{jk}} r_{jk}^2 \mathrm{d}r_{jk} = \dfrac{4\pi}{h} \Big (\dfrac{a}{\pi} \Big )^\frac{3}{2} \int_0^\infty r_{jk}e^{-ar_{jk}^2} \sin{hr_{jk}} \mathrm{d}r_{jk}
$$
$${a}$$は式(3)で定義されています。公式を使うために、積分変数の変換をします:$${x = \sqrt{a} r_{jk}}$$。$${\mathrm{d}r_{jk} = \mathrm{d}x/\sqrt{a}}$$
$$
\langle e^{-i\boldsymbol{h} \cdot \boldsymbol{r}_{jk}} \rangle = \dfrac{4\pi}{h} \Big (\dfrac{a}{\pi} \Big )^\frac{3}{2}\cdot \dfrac{1}{a} \displaystyle \int_0^\infty x e^{-x^2} \sin \Big(\dfrac{h}{\sqrt{a}} x\Big) \mathrm{d}x
$$
ここで公式[5]を用い、公式で$${b=h/\sqrt{a}}$$とおき、$${a}$$を最後に元に戻すと、
$$
\langle e^{-i\boldsymbol{h} \cdot \boldsymbol{r}_{jk}} \rangle = \dfrac{4\pi}{h} \Big (\dfrac{a}{\pi} \Big )^\frac{3}{2}\cdot \dfrac{1}{a} \cdot \dfrac{\sqrt{\pi}h}{4\sqrt{a}} \cdot \exp{\Big(-\dfrac{h^2}{4a}} \Big )= \exp{\Big ( -\dfrac{nl^2}{6} h^2\Big ) }
$$
となります。今、$${n=|k-j|}$$ですから、結局
$$
\langle e^{-i\boldsymbol{h} \cdot \boldsymbol{r}_{jk}} \rangle = \exp{\big ( -\dfrac{|k-j|l^2 }{6} h^2 \big ) }
$$
もう一度、式(4)を書くと、
$$
I(h) = A_e^2 f^2\displaystyle\sum_{j=1}^N\displaystyle\sum_{k=1}^N \exp{\big ( -\dfrac{|k-j|l^2}{6} h^2\big ) }
$$
これで行程の半分まで来ました。今度は2重の総和を求めます。総和は$${(j,k)}$$の組み合わせでとっていきます。例えていえば、
$$
総和 = (1,1) + (1,2) + (1,3) + \cdots + (2,1) + (2,2) + (2,3) + \cdots + (N,N)
$$
これを図で表すと、図3のような格子点で表すこともできます。全部で$${N \times N = N^2}$$個の格子点です。
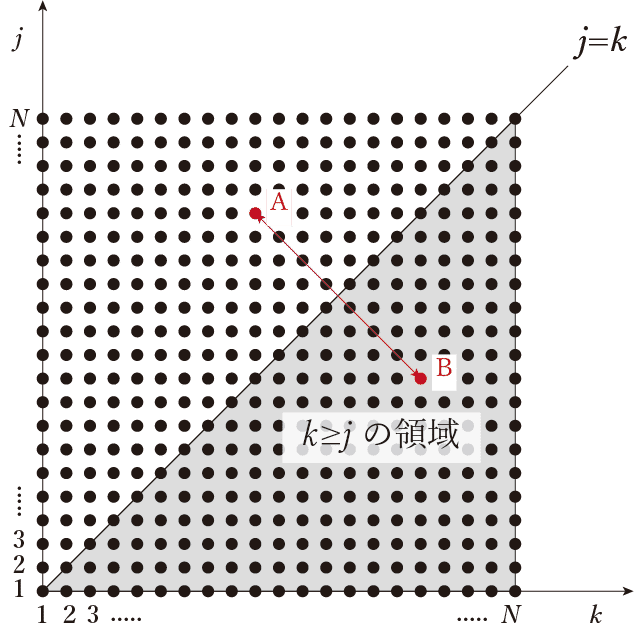
ここで、高分子鎖を考えると、$${N \gg 1}$$($${N^2 \gg N}$$)だから、近似的に総和を積分に変えることができます(図3の灰色部分が積分範囲)[6]:
$$
\displaystyle\sum_{j=1}^N\displaystyle\sum_{k=1}^N \exp{\big ( -\dfrac{|k-j|l^2}{6} h^2\big ) } \simeq 2\displaystyle \int_{k=0}^N \int_{j=0}^k \exp{\big ( -\dfrac{(k-j)l^2}{6} h^2\big ) } \mathrm{d}k \mathrm{d}j
$$
ここで式を見やすくするために、
$$
\alpha = \dfrac{l^2 h^2}{6}
$$
とおいて、
$$
2\displaystyle \int_{k=0}^N \int_{j=0}^k \exp{\big [ -\alpha(k-j)\big ] } \mathrm{d}k \mathrm{d}j = 2\int_0^N e^{-\alpha k} \Big [ \int_0^k e^{\alpha j} \mathrm{d}j \Big ] \mathrm{d}k =\\ =\dfrac{2}{\alpha}\int_0^N e^{-\alpha k} (e^{\alpha k}-1) \mathrm{d}k = \dfrac{2}{\alpha} \int_0^N (1-e^{-\alpha k}) \mathrm{d}k = \\ =\dfrac{2}{\alpha} \bigg [k+ \dfrac{e^{-\alpha k}}{\alpha} \bigg ]_0^N = \dfrac{2}{\alpha} \Big (N+\dfrac{e^{- \alpha N} }{\alpha}- \dfrac{1}{\alpha} \Big )
$$
さらに、先を見越して仮に$${R}$$を次のように定義します(後で$${R=R_G}$$であることがわかります):
$$
R^2 = \dfrac{Nl^2}{6}
$$
こうすることで、$${\alpha = R^2h^2/N}$$となり、次式を得ます:
$$
\dfrac{2}{\alpha} \Big (N+\dfrac{e^{- \alpha N}}{\alpha} - \dfrac{1}{\alpha} \Big ) = \\ =\dfrac{2}{\alpha^2} \Big ( \alpha N + e^{-\alpha N}-1 \Big ) = \dfrac{2N^2}{(R h)^4} \Big [(Rh)^2+e^{-(R h)^2} - 1 \Big]
$$
結局、問1の結果$${N_e = fN}$$も使って、
$$
I(h) = A_e^2 N_e^2 \dfrac{2}{(R_Gh)^4} \Big [ (R_Gh)^2+e^{-(R_Gh)^2} - 1 \Big] \;\;\;\;\;\;\; (答)(5)
$$
後出しジャンケンで、$${R=R_G}$$を使いました。
$${x = (R h)^2}$$とおくと、上式(5)の関数部分は、
$$
\dfrac{2}{x^2} \big ( e^{-x} + x -1)
$$
これをべき級数展開します。指数関数のべき級数展開の公式[7]を使えば、$${x \ll 1}$$のとき、
$$
\dfrac{2}{x^2} \big ( e^{-x} + x -1) = \dfrac{2}{x^2} \big (1-x+\dfrac{x^2}{2} - \dfrac{x^3}{6} + \dfrac{x^4}{24} - \cdots + x - 1 \big ) =\\ = 1 - \dfrac{x}{3} + \dfrac{x^2}{12} -\cdots \;\;\;\;\; (6)
$$
を得ます。$${h \rightarrow 0}$$とき、$${x \rightarrow 0}$$だから、
$$
I(0) = \displaystyle \lim_{h \to 0} I(h) = A_e^2 N_e^2
$$
(問4) 問3の結果を使うと、散乱関数$${P(h) = I(h)/I(0)}$$は、
$$
P(h) = \dfrac{2}{x^2} \big ( e^{-x} + x -1) \; , \;\;\;\;\; (x=R_G^2 h^2) \;\;\;\;\;(答)
$$
(問5) 式(6)から、
$$
P(h) = 1 - \dfrac{R^2}{3} h^2 + O(h^4)
$$
$${O}$$はランダウの記号で、$${O(h^4)}$$は$${h^4}$$以降の高次項を示します。上式から[8]、次式が得られます:
$$
\ln P(h) = - \dfrac{R^2}{3} h^2 + O(h^4)
$$
Guinierの法則は[1]、
$$
\ln P(h) = - \dfrac{R_G^2}{3} h^2 + \cdots
$$
だから、$${h^2}$$の係数を比べると、
$$
R_G^2 = R^2 = \dfrac{Nl^2}{6} \;\;\;\;\;\; (答)
$$
(別法)回転半径$${R_G}$$の定義は、
$$
R_G^2=\displaystyle\frac{\sum_{k}\sum_{j}f_kf_j\langle |\boldsymbol{r}_k-\boldsymbol{r}_j|^2 \rangle}{2\sum_{k}\sum_{j}f_kf_j} = \displaystyle\frac{f^2\sum_{k}\sum_{j} \langle |\boldsymbol{r}_k-\boldsymbol{r}_j|^2 \rangle}{2f^2N^2} = \\ = \displaystyle\frac{\sum_{k}\sum_{j}\langle |\boldsymbol{r}_k-\boldsymbol{r}_j|^2 \rangle}{2N^2} \;\;\;\;\;\; (7)
$$
ここでも問1と同じように、$${f_j = f_k = f}$$を使いました。
ガウス鎖の場合は絶えず形を変えているから、回転半径は平均として定義されます。本来なら、$${\langle R_G^2 \rangle}$$と表記されるべきですが、慣例に従って平均後も単に$${R_G}$$と表記します。
式(7)で問題となるのは、平均をとる$${|\boldsymbol{r}_k - \boldsymbol{r}_j|^2}$$の部分です:
$$
\langle |\boldsymbol{r}_k - \boldsymbol{r}_j|^2 \rangle = \langle \boldsymbol{r}_{jk}^2 \rangle = \langle r_{jk}^2 \rangle
$$
(問2)と同じように、
$$
\langle r_{jk}^2 \rangle = \displaystyle \int_{r_{jk}=0}^\infty \int_{\theta=0}^\pi \int_{\varphi=0}^{2\pi} r_{jk}^2W(r_{jk}) r_{jk}^2 \sin\theta \mathrm{d}r_{jk}\mathrm{d}\theta\mathrm{d}\varphi
$$
被積分関数は方角$${\theta, \varphi}$$には無関係だから、方角に関する積分を先に実行して、$${4\pi}$$を得ます。積分変数$${r_{jk}}$$は見にくいから、単に$${r}$$と変えます。$${a}$$を使えば、
$$
W(r) = \Big (\dfrac{a}{\pi} \Big )^{\frac{3}{2}} \exp{(-ar^2)}
$$
だから、
$$
\langle r_{jk}^2 \rangle = 4\pi \displaystyle \int_0^\infty r^4 W(r) \mathrm{d}r = \\ =4\pi \displaystyle \int_0^\infty r^4 \Big ( \dfrac{a}{\pi} \Big )^\frac{3}{2} e^{-ar^2} \mathrm{d}r =4\pi \Big ( \dfrac{a}{\pi} \Big )^\frac{3}{2} \int_0^\infty r^4 e^{-ar^2} \mathrm{d}r
$$
ここで、$${a}$$は、式(3)と同じ意味です:
$$
a = \dfrac{3}{2|k-j|l^2}
$$
積分公式[4]を使います:
$$
\displaystyle \int_0^\infty r^4 e^{-ar^2} \mathrm{d}r = \dfrac{3\sqrt{\pi}}{8} a^{-\frac{5}{2}}
$$
こうして、
$$
\langle r_{jk}^2 \rangle = 4\pi \Big ( \dfrac{a}{\pi} \Big )^\frac{3}{2} \times \dfrac{3\sqrt{\pi}}{8} a^{-\frac{5}{2}} = \dfrac{3}{2} a^{-1} = |k-j|l^2
$$
問3と同じように、2重の総和を積分に置き換えます:
$$
\displaystyle\sum_{j=1}^N\displaystyle\sum_{k=1}^N |k-j|l^2 = 2l^2\displaystyle \int_0^N \bigg [\int_0^k (k-j) \mathrm{d}j \bigg ] \mathrm{d}k = 2l^2 \int_0^N \bigg [kj - \dfrac{j^2}{2} \bigg ]_0^k \mathrm{d}k = \\ = 2l^2 \int_0^N \dfrac{k^2}{2} \mathrm{d}k = 2l^2 \cdot \bigg [ \dfrac{k^3}{6} \bigg ]_0^N = \dfrac{N^3}{3} l^2
$$
上式の結果を式(7)に代入して、
$$
R_G^2= \displaystyle\frac{\sum_{k}\sum_{j}\langle |\boldsymbol{r}_k-\boldsymbol{r}_j|^2 \rangle}{2N^2} = \dfrac{(N^3 l^2/3)}{2N^2} = \dfrac{Nl^2}{6} \;\;\;\;\;\; (答)
$$
図4に、ガウス鎖の散乱関数を示しました。

(終)
文献
[1] 小角X線散乱(SAXS)(1) - 基本的なこと(note記事)
[2] 小角X線散乱(SAXS)(5)- 座標系と体積要素(体積素片)dr(note記事)
[3] 例えば、$${x = \cos\theta}$$と置換すれば、$${\mathrm{d}x = - \sin\theta \mathrm{d}\theta}$$だから、
$$
\displaystyle \int_0^\pi \sin\theta \mathrm{d}\theta = - \int_1^{-1} \mathrm{d}x = \int_{-1}^1 \mathrm{d}x = \bigg [ x \bigg ]_{-1}^1 = 1-(-1) = 2
$$
[4] 森口繁一、宇田川銈久、一松信、数学公式Ⅰ(岩波全書)、岩波書店、1956.
$$
\displaystyle \int_0^\infty e^{-ax^2} x^{2n} \mathrm{d}x = \dfrac{(2n-1)!!}{2^{n+1}} \sqrt {\dfrac{\pi}{a^{2n+1}}} \;\;\;\;\;\;\;\;\; (a>0)
$$
ここでは、$${n=1}$$とおく:
$$
\displaystyle \int_0^\infty e^{-ax^2} x^2 \mathrm{d}x = \dfrac{1}{4} \sqrt {\dfrac{\pi}{a^3}} \;\;\;\;\;\;\;\;\; (a>0)
$$
[5] 同上.
$$
\displaystyle \int_0^\infty xe^{-x^2} \sin bx = \dfrac{\sqrt{\pi}b}{4} e^{-\frac{b^2}{4}}
$$
[6] 総和を積分に変える例を示します。
$$
\displaystyle \sum_{k=1}^N k \simeq \int_0^N k \mathrm{d}k
$$
上式の左辺は、$${N(N+1)/2}$$です。右辺は、
$$
\displaystyle \int_0^N k \mathrm{d}k = \bigg [ \dfrac{k^2}{2} \bigg ]_0^N = \dfrac{N^2}{2}
$$
左辺と右辺の違いは、$${N/2}$$です。$${N}$$が大きくなると、相対的にこの違いが小さくなります:
$$
\displaystyle \lim_{N \to \infty} \dfrac{N(N+1)/2}{N^2/2} = \lim_{N \to \infty} \Big(1+\dfrac{1}{N} \Big) = 1
$$
この状況を図で示すと、

[7] 森口繁一、宇田川銈久、一松信、数学公式Ⅱ(岩波全書)、岩波書店、1957.
$$
e^x = \displaystyle \sum_{n=0}^\infty \dfrac{x^n}{n!} = 1 + \dfrac{x}{1!} + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + \cdots \;\;\;\;\;\; [|x|<\infty]
$$
[8] 同上.
$$
\ln (1-x) = - \displaystyle \sum_{n=1}^\infty \dfrac{x^n}{n} = - x - \dfrac{x^2}{2} - \cdots \;\;\;\;\;\;\; [|x| \leq 1, x \neq 1]
$$
様々な形状の散乱関数(形状因子、干渉因子)
【免責事項】本記事は単なるメモとして書かれたもので、その正確性を必ずしも保証するものではありません。本記事によって生じたトラブル、損失、又は損害に対して一切責任を負いません。また、著者が所属する組織とは関係ありません。誤りがあればご指摘ください。クレームはご遠慮ください。
