Mie散乱（１）- 基本式

一見するとMie散乱の計算は難しそうですが、Pythonを使えば比較的簡単に計算できます。私なりに備忘録として何回かに分けてまとめてみました。

１．前提となる光学系

入射光はz軸方向に進み、x-z平面内でx軸方向に直線偏光している。原点に球形の粒子があり、光を散乱している。散乱光は点Pで検出される。図はφ=90°の場合に相当、y-z平面が散乱面となる。

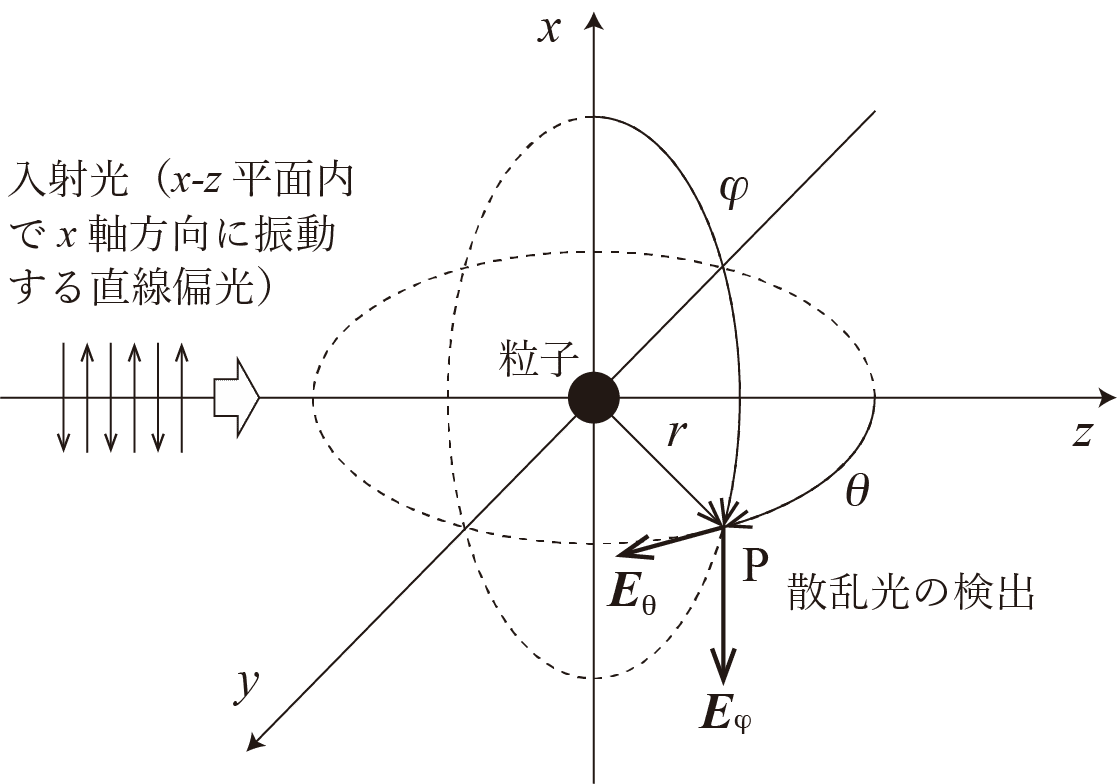
２．数式[1]

2.1 目標

目標は、以下の$${i_2(\theta)}$$、$${i_1(\theta)}$$、そして次節の$${Q_{\mathrm{ext}}}$$を計算すること：

$$
I=\frac{I_0F(\theta,\varphi)}{k^2r^2}
$$

$${I}$$：検出される散乱光強度、$${I_0}$$：入射光強度、$${k}$$：波数ベクトルの絶対値、$${r}$$：粒子から検出器までの距離、$${F(\theta,\varphi)}$$：角度のみに依存する関数、

$$
F(\theta,\varphi)=i_2(\theta)\cos^2\varphi+i_1(\theta)\sin^2\varphi
$$

（$${i_1(\theta)}$$、$${i_2(\theta)}$$は、それぞれ検出された散乱光の垂直成分と水平成分。次節で定義。）

1) 波数ベクトル$${\boldsymbol k}$$の絶対値$${k}$$：

$$
k(=|\boldsymbol k|)=\frac{2\pi n_0}{\lambda_0}
$$

$${n_0}$$：溶媒（水など）の屈折率、$${\lambda_0}$$：真空中での光の波長

2.2 計算式１

$$
i_1(\theta)=|S_1(\theta)|^2, 
i_2(\theta)=|S_2(\theta)|^2
$$

$$
S_1(\theta)=\sum_{n=1}^{\infty}\frac{2n+1}{n(n+1)}\{a_n\pi_n(\cos\theta)+b_n\tau_n(\cos\theta\}
$$

$$
S_2(\theta)=\sum_{n=1}^{\infty}\frac{2n+1}{n(n+1)}\{b_n\pi_n(\cos\theta)+a_n\tau_n(\cos\theta\}
$$

$$
Q_{\mathrm{ext}}=\frac{2}{x^2}\sum_{n=1}^{\infty}(2n+1)\mathrm{Re}(a_n+b_n)
$$

$${Q_{\mathrm{ext}}}$$：消散係数（extinction coefficient）、$${\mathrm{Re}}$$：実数部（ここは、$${a_n+b_n}$$の実数部をとるということ）

2.3 計算式２（anとbn）

$$
a_n=\frac{\psi_n^{'}(y)\psi_n(x)-m\psi_n(y)\psi_n^{'}(x)}{\psi_n^{'}(y)\zeta_n(x)-m\psi_n(y)\zeta_n^{'}(x)}
$$

$$
b_n=\frac{m\psi_n^{'}(y)\psi_n(x)-\psi_n(y)\psi_n^{'}(x)}{m\psi_n^{'}(y)\zeta_n(x)-\psi_n(y)\zeta_n^{'}(x)}
$$

$$
x=ka=\frac{2\pi n_0}{\lambda_0}a,  y=mka=mx
$$

$$
\psi_n(z)=zj_n(z)
$$

$$
\zeta_n(z)=\psi_n(z)-izn_n(z)
$$

$${a}$$：粒子の半径、$${m}$$：溶媒に対する粒子の相対屈折率（$${m=n_1/n_0}$$；$${n_1}$$：粒子の屈折率（吸収する場合は複素数））、$${j_n(z)}$$：球ベッセル関数（spherical Bessel function）[4]、$${n_n(z)}$$：球ノイマン関数（spherical Neumann funcntion）[4]、$${'}$$は微分を表す。

1) $${a_n}$$と$${b_n}$$の定義が文献によって異なります[1~3]。ここでは、文献[1]に従いました。
2) 球ベッセル関数 $${j_n(z)=\sqrt{\displaystyle\frac{\pi}{2z}}J_{n+1/2}(z)}$$、球ノイマン関数 $${n_n(z)=\sqrt{\displaystyle\frac{\pi}{2z}}N_{n+1/2}(z)}$$ [4]
3) $${z}$$は複素数です。粒子に吸収がある場合は、$${n_1}$$が複素数になるので、$${y}$$、$${a_n}$$、$${b_n}$$も複素数になります。

2.4 計算式３（πnとτn）

$$
\pi_n(\cos\theta)=\frac{1}{\sin\theta}P_n^1(\cos\theta)
$$

$$
\tau_n(\cos\theta)=\frac{\mathrm{d}}{\mathrm{d}\theta}P_n^1(\cos\theta)
$$

$${P_n^{m}(z)}$$：ルジャンドル陪関数（associated Legendre function）[4]

2.5 補遺

$$
E_\theta=-\frac{i}{kr}e^{-ikr+i\omega t}\cos\varphi S_2(\theta) 
$$

$$
E_\varphi=\frac{i}{kr}e^{-ikr+i\omega t}\sin\varphi S_1(\theta)
$$

1) $${E_\theta}$$：水平成分、$${E_\varphi}$$：垂直成分

$$
I(\theta,\varphi)=I_0(|E_\theta|^2+|E_\varphi|^2)=\displaystyle\frac{I_0F(\theta,\varphi)}{k^2r^2}
$$

文献

[1] H. C. van de Hulst, "Light Scattering by Small Particles", Dover, New York, 1981.（記事の表記はこの文献によります）
[2] いえやすの部屋、"電磁気学"、https://ieyasu03.web.fc2.com/（Mie散乱の詳しい導出があります。他の記事も参考になります。）
[3] 松山達、"ミーの散乱理論の導出"、粉体工学会誌、2006, 43, 115-124.（Mie散乱の詳しい導出があります。）
[4] 森口繁一、宇田川銈久、一松信、数学公式Ⅲ（岩波全書）、岩波書店、1960．

【免責事項】本記事は単なるメモとして書かれたもので、その正確性を必ずしも保証するものではありません。本記事によって生じたトラブル、損失、又は損害に対して一切責任を負いません。また、著者が所属する組織とは関係ありません。誤りがあればご指摘ください。クレームはご遠慮ください。