
小角X線散乱(SAXS)(10) - 【演習】ガウス型電子密度の散乱関数
ガウス型の電子密度分布をもつ物体の散乱関数(形状因子または干渉因子)を求める問題です。
【演習】ガウス型電子密度の散乱関数
図1のような、電子密度$${\rho (\boldsymbol{r})}$$が動径$${r}$$(原点からの距離)のガウス関数、
$$
\rho (r) = ae^{-\frac{r^2}{R^2}}
$$
になっている場合、
(問1) 全電子数$${N_e}$$を求めよ。
(問2) 構造因子$${F(h)}$$を求めよ[1]。ただし、$${h}$$は散乱ベクトル$${\boldsymbol{h}}$$の大きさである[1]。
(問3) 散乱強度$${I(h)}$$を求めよ[1]。
(問4) 散乱関数$${P(h)}$$を求めよ[1]。
(問5) 回転半径$${R_G}$$を求めよ[1]。
1) 用語の定義については、文献[1]を参考にしてください。

【解説】
(問1) 電子密度は単位体積あたりの電子の個数だから、全電子数$${N_e}$$は次の積分で与えられます:
$$
N_e = \displaystyle \int_V \rho(\boldsymbol{r}) \mathrm{d} \boldsymbol{r}
$$
この問題では、$${V}$$は全空間に及びます。電子密度は原点からの距離$${r}$$だけに依存するから、座標系に極座標系$${(r, \theta, \varphi) )}$$を選びます。
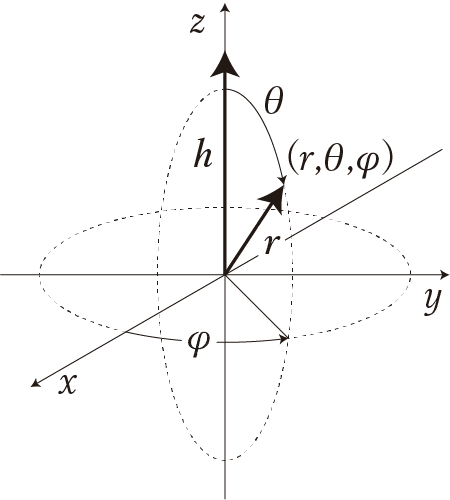
極座標系の体積要素$${\mathrm{d}\boldsymbol{r}}$$は$${r^2 \sin \theta \mathrm{d}r \mathrm{d}\theta \mathrm{d}\varphi}$$と表されました[2]。積分範囲は、$${0 \leq r < \infty}$$、$${0 \leq \theta \leq \pi}$$、$${0 \leq \varphi \leq 2\pi}$$です。上式は次のように書き換えられます:
$$
N_e = \\ = \displaystyle \int_{r=0}^\infty \int_{\theta=0}^\pi \int_{\varphi=0}^{2\pi} \rho(r) r^2 \sin \theta \mathrm{d}r \mathrm{d}\theta \mathrm{d}\varphi = \int_0^{2\pi} \mathrm{d}\varphi \int_0^\pi \sin \theta\mathrm{d}\theta \int_0^\infty ae^{-\frac{r^2}{R^2}} r^2 \mathrm{d}r
$$
ここで、
$$
\displaystyle \int_0^{2\pi} \mathrm{d}\varphi = 2\pi
$$
$$
\displaystyle \int_0^\pi \sin\theta\mathrm{d}\theta = -\displaystyle \int_0^\pi \mathrm{d}(\cos \theta) = \bigg [\cos \theta \bigg ]_\pi^0 =1-(-1) =2
$$
だから、
$$
N_e = 4\pi a\displaystyle \int_0^\infty e^{-\frac{r^2}{R^2}} r^2 \mathrm{d}r \;\;\;\;\; (1)
$$
あとは、$${r}$$に関する定積分を求めるために、公式[3]
$$
\displaystyle \int_0^\infty e^{-bx^2} x^{2n} \mathrm{d}x = \dfrac{(2n-1)!!}{2^{n+1}} \sqrt {\dfrac{\pi}{b^{2n+1}}}
$$
を用います。ここで、$${(2n-1)!!=(2n-1)(2n-3)\cdots 3 \cdot 1.}$$です。上公式で$${n=1}$$、$${b = R^{-2}}$$ とおけば、
$$
\displaystyle \int_0^\infty e^{-\frac{r^2}{R^2}} r^2 \mathrm{d}r = \dfrac{\sqrt{\pi}}{4} R^3
$$
これを式(1)に代入すると、
$$
N_e = \pi^\frac{3}{2} a R^3 \;\;\;\;\; (答)
$$
(問2) 構造因子$${F(\boldsymbol{h})}$$は[1]、
$$
F(\boldsymbol{h}) = \displaystyle \int_V \rho(\boldsymbol{r})e^{-i\boldsymbol{h} \cdot \boldsymbol{r}} \mathrm{d}\boldsymbol{r}
$$
電子密度が方角(極座標では、$${\theta}$$と$${\varphi}$$)によらず、動径$${r}$$だけに依存するので、散乱ベクトル$${\boldsymbol{h}}$$を便宜上$${z}$$軸に固定してもよさそうです(図2)。
極座標系の体積要素は$${r^2 \sin \theta \mathrm{d}r \mathrm{d}\theta \mathrm{d}\varphi}$$でしたので(上述)、
$$
F(\boldsymbol{h}) = \displaystyle \int_{r=0}^\infty \int_{\theta =0}^\pi \int_{\varphi =0}^{2\pi} \rho(r) e^{-ihr\cos\theta}r^2\sin\theta \mathrm{d}r \mathrm{d}\theta \mathrm{d}\varphi
$$
ここで、内積$${\boldsymbol{h} \cdot \boldsymbol{r}}$$は、2つのベクトル$${\boldsymbol{h}}$$、$${\boldsymbol{r}}$$がなす角が$${\theta}$$だから、$${{\boldsymbol{h} \cdot \boldsymbol{r}}=hr\cos\theta}$$。
まず被積分関数は$${\varphi}$$によらないから、上述と同じように$${\varphi}$$の積分は独立に実行できて、$${2\pi}$$が外に。次に積分変数$${\theta}$$の積分を実行する形にすると($${[ \cdots ]}$$の中)、
$$
F(\boldsymbol{h}) = F(h) = 2\pi \displaystyle \int_0^\infty \rho(r)r^2 \left[ \displaystyle \int_0^\pi e^{-ihr\cos\theta} \sin\theta \mathrm{d}\theta\right] \mathrm{d}r
$$
ここで、$${x=\cos\theta}$$とおくと、$${\mathrm{d}x = -\sin\theta \mathrm{d}\theta}$$だから、
$$
\displaystyle \int_0^\pi e^{-ihr\cos\theta} \sin\theta\mathrm{d}\theta = \displaystyle \int_{-1}^1 e^{-ihrx} \mathrm{d}x = \displaystyle \left[\frac{e^{-ihrx}}{-ihr} \right]_{-1}^1 = \\ =\displaystyle \frac{2}{hr} \frac{e^{ihr}-e^{-ihr}}{2i} = \displaystyle \frac{2\sin hr}{hr}
$$
ここでは、正弦関数(sin)の複素数による表現、
$$
\sin z = \dfrac{e^{iz} - e^{-iz}}{2i}
$$
を使いました。
こうして、電子密度が球対称の場合(方角$${\theta}$$と$${\varphi}$$によらない)[4]、
$$
F(h)=4\pi \displaystyle \int_0^\infty \rho(r)r^2 \frac{\sin hr}{hr} \mathrm{d}r
$$
これで残すは$${r}$$だけの積分になりました。上式に、$${\rho (r) = ae^{-\frac{r^2}{R^2}}}$$を代入します。さらに、$${x=r/R}$$の積分変数の変換をすると、$${r=Rx}$$、$${\mathrm{d}r = R\mathrm{d}x}$$となるから、
$$
F(h) = \dfrac{4\pi aR^2}{h} \displaystyle \int_0^\infty xe^{-x^2} \sin{(hRx)} \mathrm{d}x
$$
ここで、公式[3]
$$
\displaystyle \int_0^\infty xe^{-x^2} \sin{bx} \mathrm{d}x = \dfrac{\sqrt{\pi}b}{4} e^{-b^2/4}
$$
を利用すると、問1の答も使って、
$$
F(h) = \dfrac{4\pi aR^2}{h} \times \dfrac{\sqrt{\pi}hR}{4} e^{-\frac{(hR)^2} {4}} = \pi^{\frac{3}{2}} aR^3 e^{-\frac{(hR)^2} {4}} = \\ = N_e e^{-\frac{(hR)^2} {4}} \;\;\;\;\;\; (答)
$$
となります。
(問3) 散乱強度$${I(h)}$$は、$${I(h)=A_e^2 |F(\boldsymbol{h})|^2}$$で与えられるから[1]、
$$
I(h) = A_e^2 N_e^2 e^{-\frac{(hR)^2}{2}} \;\;\;\;\;\; (答)
$$
ここで、$${\displaystyle \lim_{ h \to 0} e^{-\frac{(hR)^2}{2}} = 1}$$だから、$${I(0) = A_e^2 N_e^2}$$が分かります。
(問4) 散乱関数$${P(h)}$$は、
$$
P(h) = I(h)/I(0)
$$
で定義されるから[1]、問3の結果を利用すれば、
$$
P(h) = e^{-\frac{(hR)^2}{2}} \;\;\;\;(答)
$$
となります。
(問5) 散乱関数$${P(h)}$$の自然対数をとると、
$$
\ln P(h) = - \dfrac{(hR)^2}{2} = - \dfrac{3R^2}{2} \times \dfrac{h^2}{3}
$$
これとGuinierの法則(Guinierプロット)[1]
$$
\ln P(h) = - \dfrac{R_G^2}{3}h^2 + \cdots
$$
と比較すると、
$$
R_G = \sqrt{\dfrac{3}{2}}R\;\;\;\;(答)
$$
(別法)球対称なので、重心は原点にありそうです($${\boldsymbol{r}_G = \boldsymbol{0}}$$)。回転半径の定義式から、
$$
R_G = \dfrac{\displaystyle \int_V \rho(\boldsymbol{r})\boldsymbol{r}^2 \mathrm{d}\boldsymbol{r}}{\displaystyle \int_V \rho(\boldsymbol{r}) \mathrm{d} \boldsymbol{r}}
$$
ここで、
$$
\displaystyle \int_V \rho(\boldsymbol{r})\boldsymbol{r}^2 \mathrm{d}\boldsymbol{r} = \displaystyle \int_{r=0}^\infty \int_{\theta =0}^{\pi} \int_{\varphi =0}^{2\pi} \rho(r) r^2 r^2\sin\theta \mathrm{d}r \mathrm{d}\theta \mathrm{d}\varphi = \\ = 4\pi a\displaystyle \int_0^\infty e^{-\frac{r^2}{R^2}}r^4 \mathrm{d}r = 4\pi \dfrac{3\sqrt{\pi}}{8} aR^5 = \dfrac{3 \pi^{\frac{3}{2}}}{2} aR^5
$$
$$
\displaystyle \int_V \rho(\boldsymbol{r}) \mathrm{d}\boldsymbol{r} = 全電子数 =4\pi a \displaystyle \int_0^\infty e^{-\frac{r^2}{R^2}} r^2 \mathrm{d}r = \pi^{\frac{3}{2}}aR^3
$$
よって、
$$
R_G^2 = \dfrac{3 \pi^{\frac{3}{2}}}{2} aR^5 \div (\pi^{\frac{3}{2}}aR^3) = \dfrac{3}{2}R^2
$$
$$
\therefore \;\;\; R_G = \sqrt{\dfrac{3}{2}}R \;\;\;\;(答)
$$
文献とNote
[1] 小角X線散乱(SAXS)(1) - 基本なこと(note記事).
[2] 小角X線散乱(SAXS)(5)- 座標系と体積要素(体積素片)dr(note記事)
[3] 森口繁一、宇田川銈久、一松信、数学公式Ⅰ(岩波全書)、岩波書店、1956.
[4] 小角X線散乱(SAXS)(6)- 【演習】 球対称の構造因子F(h)(note記事).
様々な形状の散乱関数(形状因子、干渉因子)
【免責事項】本記事は単なるメモとして書かれたもので、その正確性を必ずしも保証するものではありません。本記事によって生じたトラブル、損失、又は損害に対して一切責任を負いません。また、著者が所属する組織とは関係ありません。誤りがあればご指摘ください。クレームはご遠慮ください。
