分析化学の話（10） Z=X/Y：商の確率分布

分析化学とは直接関係ない、わき道にそれた話です。興味がなかったら、無視してください。

１．共通の疑問

1.1 共通の前提

確率変数（例：分析結果）$${Z}$$が、互いに独立な確率変数（例：測定値、データ）$${X}$$と$${Y}$$の関数になっているとします：

$$
Z = F(X, Y)　\quad \quad \quad \quad \quad \quad \quad \quad (1) 
$$

表1 各確率変数の母集団に関するパラメータ

たとえば、質量濃度$${Z}$$を求めるとき、$${X}$$を溶質の質量、$${Y}$$を溶液の体積とすれば、$${F(X,Y) = X/Y}$$となります。

1.2 共通の疑問

母集団に対して、誤差の伝播則[1, 2]に似た次の式が本当に成り立つでしょうか？

$$
\sigma^2= \bigg (\dfrac{\partial F}{\partial x} \bigg )^2 \sigma_1^2 + \bigg (\dfrac{\partial F}{\partial y} \bigg )^2 \sigma_2^2 \quad \quad \quad \quad  (2) 
$$

式(2)で注意したいのは、$${X}$$と$${Y}$$の確率密度関数$${f(x)}$$と$${g(y)}$$に無関係だということです。

1.3 結論

最初に結論をいうと、

【結論】
商 $${Z=X/Y}$$の場合、
(1) 標準偏差が通常の場合（相対標準偏差[3]が数%程度？）、誤差（不確かさ）の伝播則が成立しそうです。
(2) 標準偏差が大きい場合、誤差（不確かさ）の伝播則が少し崩れるということに留意する必要があります。

２．基礎となる式

次の式が成り立ちます[4, 5]：

$$
q(z) = \displaystyle \int_{-\infty}^\infty \int_{-\infty}^\infty\delta (z-F(x, y))f(x)g(y) \mathrm{d}x \mathrm{d}y \quad \quad \quad \quad (3)
$$

$${\delta (x)}$$：デルタ関数

３．Z=X/Y

3.1 具体的な問題の設定

$${F(x, y) = x/y}$$だから、式(3)から$${q(z)}$$は次式で与えられます：

$$
q(z) = \displaystyle \int_{-\infty}^\infty \int_{-\infty}^\infty\delta (z-(x/y))f(x)g(y) \mathrm{d}x \mathrm{d}y \quad \quad \quad \quad (4)
$$

$${\delta}$$関数の性質を使います[6]。式(A4)において$${u(x)=z-(x/y)}$$と於けば、$${u'(x)=1/y}$$であり、$${u(x)=0}$$の解$${\alpha}$$は$${zy}$$だから、

$$
q(z) = \displaystyle \int_{-\infty}^\infty |y| f(zy)g(y) \mathrm{d}y \quad \quad \quad \quad (5)
$$

$$
\mu = \displaystyle \int_{-\infty}^\infty zq(z) \mathrm{d}z \quad \quad \quad \quad (6)
$$

$$
\sigma^2 = \displaystyle \int_{-\infty}^\infty (z-\mu)^2q(z) \mathrm{d}z \quad \quad \quad \quad (7)
$$

一方、式(2)の偏微分はというと、

$$
\bigg(\dfrac{\partial F}{\partial x} \bigg)_{\mu_1, \mu_2}= \bigg(\dfrac{\partial} {\partial x} \bigg( \dfrac{x}{y} \bigg)\bigg)_{\mu_1, \mu_2}= \bigg(\dfrac{1}{y}\dfrac{\partial x}{\partial x} \bigg)_{\mu_1, \mu_2}= \bigg( \dfrac{1}{y} \bigg)_{\mu_1, \mu_2} = \dfrac{1}{\mu_2}
$$

$$
\bigg(\dfrac{\partial F}{\partial y} \bigg)_{\mu_1, \mu_2}= \bigg(\dfrac{\partial} {\partial y} \bigg( \dfrac{x}{y} \bigg)\bigg)_{\mu_1, \mu_2}= \bigg(x \dfrac{\partial}{\partial y} \bigg( \dfrac{1}{y}\bigg) \bigg)_{\mu_1, \mu_2}= \bigg( -\dfrac{x}{y^2} \bigg)_{\mu_1, \mu_2} = -\dfrac{\mu_1}{\mu_2^2}
$$

だから、式(2)に該当するのは次式です：

$$
\sigma^2= \dfrac{1}{\mu_2^2}\sigma_1^2 + \dfrac{\mu_1^2}{\mu_2^4}\sigma_2^2 \quad \quad \quad \quad  (8) 
$$

式(7)から得られた$${\boldsymbol {\sigma}}$$と、式(8)から得られた$${\boldsymbol {\sigma}}$$がどの程度一致するのかが問題となります。

3.2 正規分布の場合

3.2.1 もとの分布

$$
f(x) = \dfrac{1}{\sqrt{2\pi} \sigma_1} \exp \bigg [ - \dfrac{(x-\mu_1)^2}{2\sigma_1^2} \bigg ]\quad \quad \quad \quad (9)
$$

$$
g(y) = \dfrac{1}{\sqrt{2\pi} \sigma_2} \exp \bigg [ - \dfrac{(y-\mu_2)^2}{2\sigma_2^2} \bigg ]\quad \quad \quad \quad (10)
$$

3.2.2 $${\boldsymbol{q(z)}}$$

式(5)から出発します。式(9)と(10)を式(5)に代入すると、

$$
q(z) = \dfrac{1}{2\sigma_1 \sigma_2} \displaystyle \int_{-\infty}^\infty |y| \exp \bigg[ -\dfrac{(zy-\mu_1)^2}{2\sigma_1^2} - \dfrac{(y-\mu_2)^2}{2\sigma_2^2} \bigg] \mathrm{d}y = \\
= \dfrac{1}{2\sigma_1 \sigma_2}(q_1(z) + q_2(z))
$$

ここで、

$$
q_1(z) \equiv \displaystyle \int_0^\infty y \exp \bigg[ -\dfrac{(zy-\mu_1)^2}{2\sigma_1^2} - \dfrac{(y-\mu_2)^2}{2\sigma_2^2} \bigg] \mathrm{d}y \\
= e^a \Big( \dfrac{e^{-b^2c}}{2c} + \dfrac{b}{2}\sqrt{\dfrac{\pi}{c}} \mathrm{Erfc} (-b\sqrt{c}) \Big)
$$

$$
q_2(z) \equiv \displaystyle \int_{-\infty}^0 (-y) \exp \bigg[ -\dfrac{(zy-\mu_1)^2}{2\sigma_1^2} - \dfrac{(y-\mu_2)^2}{2\sigma_2^2} \bigg] \mathrm{d}y
\\
= \displaystyle \int_0^\infty y \exp \bigg[ -\dfrac{(zy + \mu_1)^2}{2\sigma_1^2} - \dfrac{(y + \mu_2)^2}{2\sigma_2^2} \bigg] \mathrm{d}y
\\
= e^a \Big( \dfrac{e^{-b^2c}}{2c} - \dfrac{b}{2}\sqrt{\dfrac{\pi}{c}} \mathrm{Erfc} (b\sqrt{c}) \Big)
$$

となります。
　よって、

$$
q(z) = \dfrac{e^a}{2\sigma_1 \sigma_2} \bigg[ \dfrac{e^{-b^2c}}{c} + \dfrac{b}{2} \sqrt{\dfrac{\pi}{c}} \Big( \mathrm{Erfc}(-b\sqrt{c}) - \mathrm{Erfc}(b\sqrt{c}) \Big) \bigg] \quad \quad \quad (11)
$$

となります[7]。ここで、$${\mathrm{Erfc}(x)}$$は相補誤差関数[8]です。$${a}$$、$${b}$$、$${c}$$は$${z}$$の関数であり、以下のように定義しました：

$$
a (= a(z)) = \dfrac{ \dfrac{(\mu_1 \sigma_2^2 z + \mu_2 \sigma_1^2)^2}{\sigma_2^2 z^2 + \sigma_1^2} - (\mu_1^2 \sigma_2^2 + \mu_2^2 \sigma_1^2)}{2 \sigma_1^2 \sigma_2^2}
$$

$$
b (= b(z)) = \dfrac{\mu_1 \sigma_2^2 z + \mu_2 \sigma_1^2}{\sigma_2^2 z^2 + \sigma_1^2}
$$

$$
c (= c(z)) = \dfrac{\sigma_2^2 z^2 + \sigma_1^2}{2 \sigma_1^2 \sigma_2^2}
$$

式(11)は解析的に積分を実行できないので、Pythonで数値積分を行うことにしました。

3.2.3 平均値と標準偏差
式(11)で与えられた$${q(z)}$$を使って、

$$
\mu = \displaystyle \int_{-\infty}^\infty zq(z) \mathrm{d}z \quad \quad \quad (12)
$$

$$
\sigma^2 = \displaystyle \int_{-\infty}^\infty (z-\mu)^2q(z) \mathrm{d}z \quad \quad \quad (13)
$$

もPythonで数値積分しました。

3.2.4 グラフ
i) 極端な例（XとYの相対標準偏差が各10%と20%）

図1 商の分布関数q(z)（Z=X/Y）（赤）、f(x): μ1=10, σ1=1、g(y): μ2=2, σ2=0.4。q(z)_GUM（黒）は、平均値(μ)=μ1÷μ2=5で、式(8)より計算された標準偏差(σ)をもつ正規分布。この図は、XとYの相対標準偏差がそれぞれ10%と20%の極端な例です。ヒストグラム（正規乱数の数は20,000）はあきらかにq(z)と一致しています。

ii) 通常の例（XとYの相対標準偏差がともに2%）

図2 商の分布関数q(z)（Z=X/Y）（赤）、f(x): μ1=10, σ1=0.2、g(y): μ2=2, σ2=0.04。q(z)_GUM（黒）は、平均値(μ)=μ1÷μ2=5で、式(8)より計算された標準偏差(σ)をもつ正規分布。この図は、XとYの相対標準偏差がともに2%と通常の例です。ヒストグラム（正規乱数の数は20,000）は、q(z)とq(z)_GUMともに一致しています。

3.2.5 結果
図1と図2の結果をそれぞれ表にすると、

$$
\begin{array}{lcc}
\small \boldsymbol{表2}　XとYの相対標準偏差が各10％、20％  &\\
\hline \hline
\small 方法 & \small 平均値(\mu) & \small 標準偏差(\sigma)\\
\hline \hline
\small q(z)_{\mathrm{GUM}}:式(2), (8)から計算 & \small 5.00&\small 1.12 \\
\hline \small q(z)_{\mathrm{GUM}}に補正を加えた[10] & \small  5.20 &\small 1.17\\
\hline  \small q(z)から計算& \small 5.22&\small 1.30\\
\hline \small 乱数（ヒストグラム）\quad \quad & \small 5.23&\small 1.33\\
\hline
\end{array}
$$

$$
\begin{array}{lcc}
\small \boldsymbol{表3}　XとYの相対標準偏差がともに2％ & &\\
\hline \hline
\small 方法 & \small 平均値(\mu) & \small 標準偏差(\sigma)\\
\hline \hline
\small q(z)_{\mathrm{GUM}}:式(2), (8)から計算 \quad \quad \quad \quad & \small 5.000&\small 0.141 \\
\hline \small q(z)_{\mathrm{GUM}}に補正を加えた[10] & \small  5.000 &\small 0.142\\
\hline  \small q(z)から計算& \small 5.002&\small 0.142\\
\hline \small 乱数（ヒストグラム）\quad \quad & \small 5.001&\small 0.142\\
\hline
\end{array}
$$

図1のケースでは、違いを示すため、$${X}$$と$${Y}$$の標準偏差が非常に大きい（それぞれ相対標準偏差が10%と20%）極端な例を示しました。平均値も標準偏差も有意に差がついています。しかし、図2のような標準偏差が小さい通常の場合（それぞれ相対標準偏差がともに2%）、$${q(z)_{\mathrm{GUM}}}$$は、正確な$${q(z)}$$と平均値も標準偏差も一致してます。
　上記のことから、$${X}$$と$${Y}$$の標準偏差が通常の場合、誤差（不確かさ）の伝播則（式(2)、(8)）が成立していると思われます。逆に、これらの標準偏差が非常に大きい場合は、誤差（不確かさ）の伝播則から外れるということも留意する必要があります。

3.3 一様分布（矩形分布）の場合

3.3.1 もとの分布

$$
f(x) = \dfrac{1}{2a_1} \quad \quad(\mu_1 - a_1 \leq x \leq \mu_1 + a_1)\\
f(x)= 0  \quad (x<\mu_1 - a_1, \quad x> \mu_1 + a_1)
$$

$$
g(y) = \dfrac{1}{2a_2} \quad \quad(\mu_2- a_2 \leq y \leq \mu_2 + a_2)\\
g(y)= 0  \quad (x<\mu_2 - a_2, \quad y> \mu_2 + a_2)
$$

図3 f(x)とg(y)の一様分布（矩形分布）のグラフ

3.2.2 前提

$$
\mu_1 \geq \mu_2
$$

 3.2.3 $${\boldsymbol{z}}$$に関するパラメータ

$$
x_1 = \mu_1 - a_1 \\
x_2 = \mu_1 + a_1 \\
y_1 = \mu_2 - a_2 \\
y_2 = \mu_2 + a_2
$$

$$
z_1 = x_2 / y_1 \\
z_2 = x_2 / y_2 \\
z_3 = x_1 / y_1 \\
z_4 = x_1 / y_2
$$

3.2.4 $${\boldsymbol{q(z)}}$$
i) $${\boldsymbol{z_2 \leq z_3}}$$の場合：

$$
z_4 < z_2 \leq z_3 < z_1
$$

$$
q(z) = 0, \quad \quad \quad (z< z_4, \; z \geq z_1 )
$$

$$
q(z) = \dfrac{1}{4a_1a_2} \displaystyle \int_{y_1}^{x_2/z} y \mathrm{d}y = \dfrac{1}{4a_1a_2} \Big[ \dfrac{y^2}{2} \Big]_{y_1}^{x_2/z} =
\\
=\dfrac{1}{8a_1a_2} \Big( \Big(\dfrac{x_2}{z} \Big)^2 - y_1^2\Big) , \quad (z_3 \leq z < z_1)
$$

$$
q(z) =  \dfrac{1}{4a_1a_2} \displaystyle \int_{x_1/z}^{x_1/z}y \mathrm{d}y = \dfrac{1}{8a_1a_2} \Big( \dfrac{x_2^{2} - x_1^2}{z^2} \Big), \quad (z_2 \leq z < z_3 )
$$

$$
q(z) = \dfrac{1}{4a_1a_2} \displaystyle \int_{x_1/z}^{y_2} y \mathrm{d}y = \dfrac{1}{8a_1a_2} \bigg( y_2^{2} - \Big( \dfrac{x_1}{z} \Big)^2 \bigg), \quad (z_4 \leq z < z_2)
$$

図4 q(z)の計算の説明図(z2<z3)（f(x): μ1 = 4, a1 = 0.2、g(y): μ2 = 2, a2 = 0.75）。zが減少するにつれて、f(zy)（灰色）が右に移動します（(1)→(2)→…→(8)→(9)）。|y|f(zy)がg(y)と重なる場合がq(z)が0にならない場合です（|y|f(z-y)g(y)≠0、赤の部分）。z1 = 3.36, z2 = 1.53, z3 = 3.04, z4 = 1.38。積の場合と逆で、z1>z3≧z2>z4となっています。

ii) $${\boldsymbol{z_2 > z_3}}$$の場合：

$$
z_4 < z_3 < z_2 < z_1
$$

$$
q(z) = 0, \quad \quad \quad (z < z_4 , \; z \geq z_1)
$$

$$
q(z) = \dfrac{1}{4a_1a_2} \displaystyle \int_{y_1}^{x_1/z} y \mathrm{d}y = \dfrac{1}{8a_1a_2} \bigg( \Big( \dfrac{x_2}{z} \Big)^2 - y_1^2 \bigg), \quad (z_2 \leq z < z_1)
$$

$$
q(z) = \dfrac{1}{4a_1a_2} \displaystyle \int_{y_1}^{y_2} y \mathrm{d}y =  \dfrac{1}{8a_1a_2} (y_2^2 - y_1^2), \quad (z_3 \leq z < z_2)
$$

$$
q(z) = \dfrac{1}{4a_1a_2} \displaystyle \int_{x_1/z}^{y_2} y \mathrm{d}y = \dfrac{1}{8a_1a_2} \bigg( y_2^2 - \Big( \dfrac{x_1}{z} \Big)^2 \bigg), \quad (z_4 \leq z < z_3)
$$

2.4.5 平均値と標準偏差

i) $${\boldsymbol{z_2 \leq z_3}}$$の場合：
平均値$${\mu}$$：

$$
\mu = \displaystyle \int_{z_4}^{z_1} zq(z) \mathrm{d}z =
\\
= \dfrac{1}{8a_1a_2} \bigg[ x_2^2 \ln \Big( \dfrac{z_1}{z_3} \Big) - \dfrac{y_1^2(z_1^2 - z_3^2)}{2} + (x_2^2 - x_1^2)\ln \Big( \dfrac{z_3}{z_2} \Big) + \\ + \dfrac{y_2^2(z_2^2 - z_4^2)}{2} - x_1^2 \ln \Big( \dfrac{z_2}{z_4} \Big) \bigg]
$$

標準偏差$${\sigma}$$：

$$
\sigma^2 = \displaystyle \int_{z4}^{z1} (z-\mu)^2q(z) \mathrm{d}z = \bar{z^2} - \mu^2
$$

ここで、

$$
\bar{z^2} = \dfrac{1}{8a_1a_2} \bigg[ x_2^2(z_1 - z_3) - \dfrac{y_1^2(z_1^3 - z_3^3)}{3} + (x_2^2 - x_1^2)(z_3 - z_2) +
\\
＋\dfrac{y_2^2(z_2^3 - z_4^3)}{3} - x_1^2(z_2 - z_4)\bigg]
$$

ii) $${\boldsymbol{z_2 > z_3}}$$の場合：
平均値$${\mu}$$：

$$
\mu = \displaystyle \int_{z_4}^{z_1} zq(z) \mathrm{d}z =
\\
=\dfrac{1}{8a_1a_2} \bigg[ x_2^2 \ln \Big( \dfrac{z_1}{z_2} \Big) - \dfrac{y_1^2(z_1^2 - z_2^2)}{2} + \dfrac{(y_2^2 - y_1^2)(z_2^2 - z_3^2)}{2} +
\\
＋\dfrac{y_2^2(z_3^2 - z_4^2)}{2} - x_1^2 \ln \Big( \dfrac{z_3}{z_4} \Big) \bigg]
$$

標準偏差$${\sigma}$$：

$$
\sigma^2 = \displaystyle \int_{z4}^{z1} (z-\mu)^2q(z) \mathrm{d}z = \bar{z^2} - \mu^2
$$

$$
\bar{z^2} = \dfrac{1}{8a_1a_2} \bigg[ x_2^2(z_1 - z_2) - \dfrac{y_1^2(z_1^3 - z_2^3)}{3} + \dfrac{(y_2^2 - y_1^2)(z_2^3 - z_3^3)}{3} + \\
+ \dfrac{y_2^2(z_3^3 - z_4^3)}{3} - x_1^2(z_3 - z_4)\bigg]
$$

2.4.6 グラフ
i) 極端な例（XとYの相対標準偏差がともに約20%）

図5 q(z)（Z=X/Y）のグラフ。q(z)がヒストグラムと一致しているのがわかります。ヒストグラムは、Pythonのモジュールnumpyの一様分布に基づく乱数から作成しました（乱数の数=40,000）。Xの一様分布f(x): μ1 = 10, a1 = 3、Yの一様分布g(y): μ2 = 5, a2 = 1.7。標準偏差が大きい（XとYの相対標準偏差がそれぞれ、17%と20%）例。z2<z3でした。 計算とヒストグラム作成はともにPythonで行いました。

ii) 通常の例（XとYの相対標準偏差がともに約2%）

図6 q(z)（Z=X/Y）のグラフ。q(z)がヒストグラムと一致しているのがわかります。ヒストグラムは、Pythonのモジュールnumpyの一様分布に基づく乱数から作成しました（乱数の数=40,000）。Xの一様分布f(x): μ1 = 10, a1 = 0.3、Yの一様分布g(y): μ2 = 5, a2 = 0.2。標準偏差が通常の（XとYの相対標準偏差がともに約2%）例。z2<z3でした。 計算とヒストグラム作成はともにPythonで行いました。

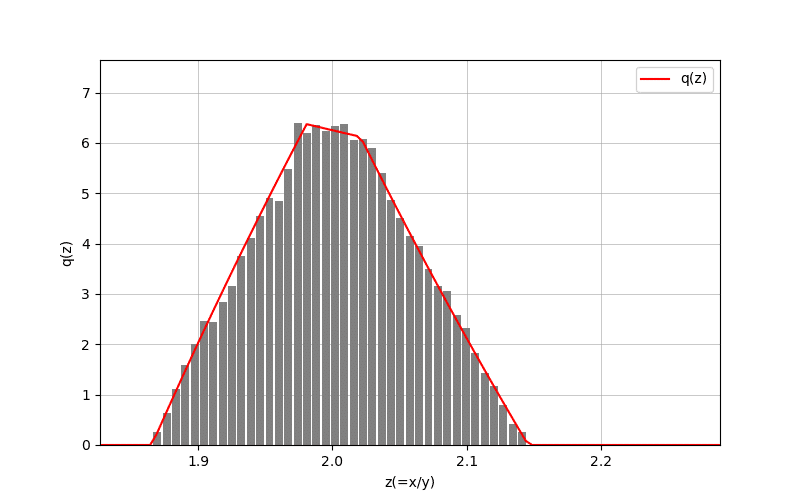
2.4.7 結果
図5と図6の結果は下の表のようでした：

$$
\begin{array}{lcc}
\small \boldsymbol{表4} 　XとYの相対標準偏差が各17％、20％& &\\
\hline \hline
\small 方法 & \small 平均値(\mu)& \small 標準偏差(\sigma)\\
\hline \hline
\small q(z)_{\mathrm{GUM}}:式(2)または(8)から計算 & \small 2&\small 0.524 \\
\hline \small q(z)_{\mathrm{GUM}}に補正を加えた[10] & \small  2.077 &\small 0.538\\
\hline  \small q(z)から計算& \small 2.083&\small 0.566\\
\hline \small 乱数（ヒストグラム）\quad \quad & \small 2.088&\small 0.565\\
\hline
\end{array}
$$

$$
\begin{array}{lcc}
\small \boldsymbol{表5}  XとYの相対標準偏差がともに約2％& &\\
\hline \hline
\small 方法 & \small 平均値(\mu) & \small 標準偏差(\sigma)\\
\hline \hline
\small q(z)_{\mathrm{GUM}}:式(2)または(8)から計算 & \small 2&\small 0.0577 \\
\hline \small q(z)_{\mathrm{GUM}}に補正を加えた[10] & \small  2.001 &\small 0.0578\\
\hline  \small q(z)から計算& \small 2.001&\small 0.0578\\
\hline \small 乱数（ヒストグラム）\quad \quad & \small 2.002&\small 0.0578\\
\hline
\end{array}
$$

図5のケースでは、$${X}$$と$${Y}$$の標準偏差が非常に大きい極端な例を示しました。平均値も標準偏差も有意に差がついています。しかし、図6のような標準偏差が通常の場合、$${q(z)_{\mathrm{GUM}}}$$は、正確な$${q(z)}$$と平均値も標準偏差も一致してます。
　上記のことから、もとの分布が正規分布と同じように、一様分布の場合も、$${X}$$と$${Y}$$の標準偏差が通常の場合、誤差（不確かさ）の伝播則（式(2)、(8)）が成立していると思われます。逆に、これらの相対標準偏差が非常に大きい場合は、誤差（不確かさ）の伝播則から外れるということも留意する必要があります。

文献とNote

[1] 誤差の伝播則、あるいは不確かさの合成は、標準不確かさ$${u}$$を用いて次式のように表されます：

$$
u^2(z)= \bigg (\dfrac{\partial F}{\partial x} \bigg )^2 u^2(x) + \bigg (\dfrac{\partial F}{\partial y} \bigg )^2 u^2(y) \quad \quad \quad \quad  (\mathrm{A}1) 
$$

標準不確かさは標準偏差と同じような意味を持っています。
[2] ISO, Guide to the Expression of Uncertainty in Measurement (1995). 略して、"GUM".　誤差（不確かさ）の伝播則に従う確率密度関数に下付きの添え字"GUM"をつけました。
[3] 相対標準偏差 = 標準偏差 ÷ 平均値
[4] 緑川章一、"確率変数の和，積，商，べき乗の分布".
[5] 早川美徳、"Pythonプログラミング（ステップ７・確率密度関数とその計算）" Feb. 15, 2022.
[6] $${\delta}$$関数の性質：

$$
\delta (-x) = \delta (x) \quad \quad \quad \quad (\mathrm{A}2)
$$

$$
\displaystyle \int_{-\infty}^\infty \delta(x-a)f(x) \mathrm{d}x = f(a)\quad \quad \quad \quad (\mathrm{A}3)
$$

$$
\delta(ax) = \dfrac{1}{|a|} \delta(x)\quad \quad \quad \quad (\mathrm{A}4)
$$

$$
\delta (u(x)) = \dfrac{1}{|u'(\alpha)|} \delta(x-\alpha)　\quad \quad \quad \quad (\mathrm{A}5)
$$

ただし、$${\alpha}$$は、$${u(x)=0}$$を$${x}$$の方程式とみた解。
[7] たとえば、$${q_1(z)}$$の途中計算を以下に示します。蛇足かもしれませんが。

$$
q_1(z) = \displaystyle \int_0^\infty y \exp \Big[ - \dfrac{(zy-\mu_1)^2}{2\sigma_1^2} - \dfrac{(y-\mu_2)^2}{2\sigma_2^2} \Big] \mathrm{d}y
\\
= \int_0^\infty y \exp \Big[ - \dfrac{\sigma_2^2(zy-\mu_1)^2 + \sigma_1^2(y-\mu_2)^2}{2\sigma_1^2 \sigma_2^2} \Big] \mathrm{d}y
\\
= \int_0^\infty y\exp \Big[- \dfrac{(\sigma_2^2z^2 + \sigma_1^2)y^2 - 2(\mu_1 \sigma_2^2z + \mu_2 \sigma_1^2)y + \mu_1^2 \sigma_2^2 + \mu_2^2 \sigma_1^2}{2 \sigma_1^2 \sigma_2^2} \Big] \mathrm{d}y
$$

ここで被積分関数の分子の$${y}$$に関する完全平方の形を目指せば、

$$
q_1(z) = \exp \bigg[\dfrac{(\mu_1\sigma_2^2z+\mu_2\sigma_1^2)^2/(\sigma_2^2z^2+\sigma_1^2)-(\mu_1^2\sigma_2^2+\mu_2^2\sigma_1^2)}{2\sigma_1^2\sigma_2^2} \bigg] \times
\\
\times \displaystyle \int_0^\infty y\exp \bigg[-\dfrac{(\sigma_2^2z^2+\sigma_1^2)\Big(y-(\mu_1\sigma_2^2z+\mu_2\sigma_1^2)/(\sigma_2^2z^2+\sigma_1^2)\Big)^2}{2\sigma_1^2\sigma_2^2} \bigg]\mathrm{d}y
$$

となります。係数$${a(z)}$$、$${b(z)}$$、$${c(z)}$$を本文のように定義し、積分変数変換

$$
y' = y - b(z)
$$

すれば、

$$
q_1(z) = e^a \displaystyle \int_{-b}^\infty (y'+b)e^{-cy'^2} \mathrm{d}y' = e^a \Big(\int_{-b}^\infty y'e^{-cy'^2}\mathrm{d}y' + b\int_{-b}^\infty e^{-cy'^2}\mathrm{d}y' \Big)
$$

さらに、積分変数の変換

$$
x = \sqrt{c}\;y'
$$

をすると、

$$
q_1(z) = e^a \Big( \dfrac{1}{c}\displaystyle \int_{-b\sqrt{c}}^\infty xe^{-x^2}\mathrm{d}x + \dfrac{b}{\sqrt{c}} \int_{-b\sqrt{c}}^\infty e^{-x^2} \mathrm{d}x \Big) =
\\
= e^a \Big(\dfrac{1}{2c} \int_{b^2c}^\infty e^{-t} \mathrm{d}t + \dfrac{b}{2} \sqrt{\dfrac{\pi}{c}} \mathrm{Erfc}(-b\sqrt{c}) \Big)=
\\
=e^a \Big(\dfrac{e^{-b^2c}}{2c} + \dfrac{b}{2} \sqrt{\dfrac{\pi}{c}} \mathrm{Erfc}(-b\sqrt{c}) \Big)
$$

$${q_2(z)}$$も同様。
[8] 相補誤差関数：

$$
\mathrm{Erfc}(x) \equiv \displaystyle \dfrac{2}{\sqrt{\pi}}\int_x^\infty e^{-t^2} \mathrm{d}t
$$

Phytonでは上式で定義されています。
　ただし、次式で相補誤差関数を定義している文献[9]があるので、注意が必要です。

$$
\mathrm{Erfc}(x) \equiv \displaystyle \int_x^\infty e^{-t^2} \mathrm{d}t
$$

[9] 森口繁一、宇田川銈久、一松信、数学公式Ⅲ（岩波全書）、岩波書店、1960.
[10] 補正項：$${X}$$と$${Y}$$は互いに独立とします。Taylor展開が収束するかどうかは個人的には不明ですが、とりあえず$${F(x,y)=x/y}$$を、$${(\mu_1, \mu_2)}$$の周りで2次の項までTaylor展開してみます：

$$
F(x,y) = F(\mu_1, \mu_2) + \Big( \dfrac{\partial F}{\partial x} \Big)_{\mu_1,\mu_2}(x-\mu_1) + \Big( \dfrac{\partial F}{\partial y} \Big)_{\mu_1,\mu_2}(y-\mu_2) + \\
+ \dfrac{1}{2} \bigg[ \Big( \dfrac{\partial^2 F}{\partial x^2} \Big)_{\mu_1,\mu_2}(x-\mu_1)^2 + \bigg(\Big( \dfrac{\partial^2 F}{\partial y \partial x} \Big)_{\mu_1,\mu_2} + \Big( \dfrac{\partial^2 F}{\partial x \partial y} \Big)_{\mu_1,\mu_2} \bigg)(x-\mu_1)(y-\mu_2) \\
+  \Big( \dfrac{\partial^2 F}{\partial y^2} \Big)_{\mu_1,\mu_2}(y-\mu_2)^2 \bigg] \quad \quad \quad (\mathrm{A}1)
$$

ここで、

$$
(\partial F/\partial x)_{\mu_1,\mu_2} = (1/y)_{\mu_1,\mu_2}=1/\mu_2 \\
(\partial F/\partial y)_{\mu_1,\mu_2} = (-x/y^2)_{\mu_1,\mu_2}=-\mu_1/\mu_2^2 \\
(\partial^2 F/\partial x^2)_{\mu_1,\mu_2} = 0 \\
(\partial^2 F/\partial y\partial x)_{\mu_1,\mu_2} =(-1/y^2)_{\mu_1,\mu_2} = -1/\mu_2^2 \\
(\partial^2 F/\partial x\partial y)_{\mu_1,\mu_2} =(-1/y^2)_{\mu_1,\mu_2} = -1/\mu_2^2 \\ 
(\partial^2 F/\partial y^2)_{\mu_1,\mu_2} = (2x/y^3)_{\mu_1,\mu_2} = 2\mu_1/\mu_2^3 \\
$$

だから、これらを式(A1)に代入すると、

$$
F(x,y) = \dfrac{\mu_1}{\mu_2} + \dfrac{1}{\mu_2}(x-\mu_1) - \dfrac{\mu_1}{\mu_2^2}(y-\mu_2) - \dfrac{1}{\mu_2^2}(x-\mu_1)(y-\mu_2) + \\
+ \dfrac{\mu_1}{\mu_2^3}(y-\mu_2)^2
$$

となります。まず、$${Z}$$の平均値$${\mu}$$は、

$$
\mu = \displaystyle \int_{-\infty}^\infty \int_{-\infty}^\infty F(x,y)f(x)g(y) \mathrm{d}x \mathrm{d}y = \\
= \dfrac{\mu_1}{\mu_2} + \dfrac{\mu_1}{\mu_2^3} \int_{-\infty}^\infty (y-\mu_2)^2g(y) \mathrm{d}y = \dfrac{\mu_1}{\mu_2} + \dfrac{\mu_1}{\mu_2^3}\sigma_2^2
$$

標準偏差$${\sigma}$$は、

$$
\sigma^2 = \displaystyle \int_{-\infty}^\infty \int_{-\infty}^\infty \Big[F(x,y)-F(\mu_1, \mu_2) \Big]^2 f(x)g(y) \mathrm{d}x \mathrm{d}y \\
=\int_{-\infty}^\infty \int_{-\infty}^\infty \Big[ \dfrac{1}{\mu_2}(x-\mu_1) - \dfrac{\mu_1}{\mu_2^2}(y-\mu_2) - \dfrac{1}{\mu_2^2}(x-\mu_1)(y-\mu_2) + \\
+ \dfrac{\mu_1}{\mu_2^3}(y-\mu_2)^2\Big]^2 f(x)g(y) \mathrm{d}x \mathrm{d}y
$$

$$
2乗項=\dfrac{1}{\mu_2^2}\displaystyle \int_{-\infty}^\infty \int_{-\infty}^\infty (x-\mu_1)^2 f(x)g(y)\mathrm{d}x\mathrm{d}y + \\
+ \dfrac{\mu_1^2}{\mu_2^4}\int_{-\infty}^\infty \int_{-\infty}^\infty (y-\mu_2)^2 f(x)g(y)\mathrm{d}x\mathrm{d}y +\\
+ \dfrac{1}{\mu_2^4}\int_{-\infty}^\infty \int_{-\infty}^\infty (x-\mu_1)^2(y-\mu_2)^2 f(x)g(y)\mathrm{d}x\mathrm{d}y + \\
+ \dfrac{\mu_1^2}{\mu_2^6} \int_{-\infty}^\infty \int_{-\infty}^\infty (y-\mu_2)^4 f(x)g(y)\mathrm{d}x\mathrm{d}y +\\
= \dfrac{\sigma_1^2}{\mu_2^2} + \dfrac{\mu_1^2 \sigma_2^2}{\mu_2^4} + \dfrac{\sigma_1^2 \sigma_2^2}{\mu_2^4} + \dfrac{\mu_1^2}{\mu_2^6} \int_{-\infty}^\infty \int_{-\infty}^\infty (y-\mu_2)^4 f(x)g(y)\mathrm{d}x\mathrm{d}y
$$

$$
交差項= - \dfrac{2\mu_1}{\mu_2^3} \displaystyle \int_{-\infty}^\infty \int_{-\infty}^\infty(x-\mu_1)(y-\mu_2)f(x)g(y)\mathrm{d}x\mathrm{d}y \\
- \dfrac{2}{\mu_2^3} \int_{-\infty}^\infty \int_{-\infty}^\infty(x-\mu_1)^2(y-\mu_2)f(x)g(y)\mathrm{d}x\mathrm{d}y \\
+ \dfrac{2\mu_1}{\mu_2^4}\int_{-\infty}^\infty \int_{-\infty}^\infty(x-\mu_1)(y-\mu_2)^2f(x)g(y)\mathrm{d}x\mathrm{d}y \\
+ \dfrac{2\mu_1}{\mu_2^4} \int_{-\infty}^\infty \int_{-\infty}^\infty(x-\mu_1)(y-\mu_2)^2f(x)g(y)\mathrm{d}x\mathrm{d}y \\
- \dfrac{2\mu_1^2}{\mu_2^5} \int_{-\infty}^\infty \int_{-\infty}^\infty(y-\mu_2)^3f(x)g(y)\mathrm{d}x\mathrm{d}y\\
- \dfrac{2\mu_1}{\mu_2^5} \int_{-\infty}^\infty \int_{-\infty}^\infty(x-\mu_1)(y-\mu_2)^3f(x)g(y)\mathrm{d}x\mathrm{d}y =\\
= 0-0+0+0- \dfrac{2\mu_1^2}{\mu_2^5} \int_{-\infty}^\infty (y-\mu_2)^3g(y)\mathrm{d}y-0 =\\
= - \dfrac{2\mu_1^2}{\mu_2^5} \int_{-\infty}^\infty (y-\mu_2)^3g(y)\mathrm{d}y
$$

よって、

$$
\sigma^2 = \dfrac{\sigma_1^2}{\mu_2^2} + \dfrac{\mu_1^2 \sigma_2^2}{\mu_2^4} + \dfrac{\sigma_1^2 \sigma_2^2}{\mu_2^4} + \dfrac{\mu_1^2}{\mu_2^6} \displaystyle \int_{-\infty}^\infty  (y-\mu_2)^4 g(y)\mathrm{d}y -\\
- \dfrac{2\mu_1^2}{\mu_2^5} \int_{-\infty}^\infty (y-\mu_2)^3g(y)\mathrm{d}y, \hspace{50pt}(\mathrm{A}2)
$$

上式では、

$$
\displaystyle \int_{-\infty}^\infty f(x) \mathrm{d}x = \int_{-\infty}^\infty g(y) \mathrm{d}y = 1\\
\displaystyle \int_{-\infty}^\infty (x-\mu_1)f(x) \mathrm{d}x = 0
$$

などを用いました。

i) 正規分布の場合：
$${f(x)}$$と$${g(y)}$$がともに正規分布の場合、その対称性から、整数$${n=0,1,2,\cdots}$$に対して、

$$
\displaystyle \int_{-\infty}^\infty (x-\mu_1)^{2n+1}f(x) \mathrm{d}x = \dfrac{1}{\sqrt{2\pi}\sigma_1} \int_{-\infty}^\infty (x-\mu_1)^{2n+1} e^{-(x-\mu_1)^2/2\sigma_1^2} \mathrm{d}x= \\
= \dfrac{1}{\sqrt{2\pi}\sigma_1} \int_{-\infty}^\infty X^{2n+1} e^{-X^2/2\sigma_1^2} \mathrm{d}X = \\
=\dfrac{1}{\sqrt{2\pi}\sigma_1} \bigg[ \int_{-\infty}^0 X^{2n+1} e^{-X^2/2\sigma_1^2} \mathrm{d}X+\int_0^\infty X^{2n+1} e^{-X^2/2\sigma_1^2} \mathrm{d}X \bigg] = \\
= \dfrac{1}{\sqrt{2\pi}\sigma_1} \bigg[-\int_0^\infty X^{2n+1} e^{-X^2/2\sigma_1^2} \mathrm{d}X+\int_0^\infty X^{2n+1} e^{-X^2/2\sigma_1^2} \mathrm{d}X \bigg] \\
= 0, \quad (n=0,1,2,\cdots)
$$

だから、奇数次の積分は0になります。このことを利用すると、式(A2)は、

$$
\sigma^2 = \dfrac{\sigma_1^2}{\mu_2^2} + \dfrac{\mu_1^2 \sigma_2^2}{\mu_2^4} + \dfrac{\sigma_1^2 \sigma_2^2}{\mu_2^4} + \dfrac{\mu_1^2}{\mu_2^6} \displaystyle \int_{-\infty}^\infty  (y-\mu_2)^4 g(y)\mathrm{d}y
$$

ここで[11]、

$$
\displaystyle \int_{-\infty}^\infty  (y-\mu_2)^4 g(y)\mathrm{d}y = \dfrac{1}{\sqrt{2\pi}\sigma_2} \int_{-\infty}^\infty  (y-\mu_2)^4 e^{-(y-\mu_2)^2/2\sigma_2^2} \mathrm{d}y= \\ =\dfrac{1}{\sqrt{2\pi}\sigma_2}  \int_{-\infty}^\infty  \eta^4 e^{-\eta^2/2\sigma_2^2} \mathrm{d}\eta =\dfrac{2}{\sqrt{2\pi}\sigma_2}\int_0^\infty  \eta^4 e^{-\eta^2/2\sigma_2^2} \mathrm{d}\eta = \\
= \dfrac{\sqrt{2}}{\sqrt{\pi}\sigma_2} \times \dfrac{3\sqrt{\pi}}{\sqrt{2}} \sigma_2^5= 3\sigma_2^4
$$

よって、

$$
\sigma^2 = \dfrac{\sigma_1^2}{\mu_2^2} + \dfrac{\mu_1^2 \sigma_2^2}{\mu_2^4} + \dfrac{\sigma_1^2 \sigma_2^2}{\mu_2^4} + \dfrac{3\mu_1^2\sigma_2^4}{\mu_2^6}
$$

結局補正項は、正規分布の場合には、

$$
補正項 = \dfrac{\sigma_1^2 \sigma_2^2}{\mu_2^4} + \dfrac{3\mu_1^2\sigma_2^4}{\mu_2^6}
$$

ii) 一様分布（矩形分布）の場合：

$$
\displaystyle \int_{-\infty}^\infty (y-\mu_2)^ng(y)\mathrm{d}y = \dfrac{1}{2a_2} \int_{\mu_2 - a_2}^{\mu_2+a_2} (y-\mu_2)^n \mathrm{d}y= \\
= \dfrac{1}{2a_2 (n+1)} \bigg[ (y-\mu_2)^{n+1} \bigg] _{\mu_2 - a_2}^{\mu_2+a_2} = \dfrac{a_2^n}{2 (n+1)} \big[ 1- (-1)^{n+1} \big]
$$

だから、式(A2)において、

$$
\displaystyle \int_{-\infty}^\infty (y-\mu_2)^3g(y)\mathrm{d}y = 0 \\
\displaystyle \int_{-\infty}^\infty (y-\mu_2)^4g(y)\mathrm{d}y = \dfrac{a_2^4}{5} = \dfrac{9\sigma_2^4}{5}
$$

ここで、一様分布（矩形分布）の場合は、

$$
\sigma_2^2 = \dfrac{a_2^2}{3}
$$

最終的に、

$$
\sigma^2 = \dfrac{\sigma_1^2}{\mu_2^2} + \dfrac{\mu_1^2 \sigma_2^2}{\mu_2^4} + \dfrac{\sigma_1^2 \sigma_2^2}{\mu_2^4} + \dfrac{9\mu_1^2\sigma_2^4}{5\mu_2^6}
$$

補正項は、

$$
補正項= \dfrac{\sigma_1^2 \sigma_2^2}{\mu_2^4} + \dfrac{9\mu_1^2\sigma_2^4}{5\mu_2^6}
$$

[11] 森口繁一、宇田川銈久、一松信、数学公式Ⅰ（岩波全書）、岩波書店、1956.

$$
\displaystyle \int_0^\infty e^{-ax^2}x^{2n} \mathrm{d}x = \dfrac{(2n-1)!!}{2^{n+1}} \sqrt{\dfrac{\pi}{a^{2n+1}}}, \quad \quad \quad (a>0, n=0,1,2,\cdots)
$$

---

【免責事項】本記事は単なるメモとして書かれたもので、その正確性を必ずしも保証するものではありません。本記事によって生じたトラブル、損失、又は損害に対して一切責任を負いません。また、著者が所属する組織とは関係ありません。誤りがあればご指摘ください。クレームはご遠慮ください。