小角X線散乱（SAXS）（15） - 【演習】針の散乱関数

2024年7月24日 15:45

無限に細い針の散乱関数（形状因子、干渉因子）を求める問題です。

【演習】針の散乱関数

図1のような、長さが$${2H}$$で無限に細い針がある。針の電子密度（単位長さあたりの電子数）は均一で$${\lambda_0}$$とする（X線の波長ではない）。また、針はランダムに配向しているとする。

このとき、
(問1) 全電子数$${N_e}$$を求めよ。
(問2) 構造因子$${F(\boldsymbol{h})}$$を求めよ。ただし、$${\boldsymbol{h}}$$は散乱ベクトルである[1]。
(問3) 散乱強度$${I(h)}$$を求めよ[1]。ただし、$${h}$$は散乱ベクトル$${\boldsymbol{h}}$$の大きさである。
(問4) 散乱関数$${P(h)}$$を求めよ[1]。
(問5) 回転半径$${R_G}$$を求めよ[1]。

1) 用語の定義については、文献[1]を参考にしてください。

【解説】
(問1) 電子密度は単位長さあたりの電子数です。針の長さは、$${2H}$$だから、

$$
N_e = 2\lambda_0 H\;\;\;\;\;\;\; （答）
$$

(問2) 図1の配向では、構造因子$${F(\boldsymbol{h})}$$は次式で与えられます[1]：

$$
F(\boldsymbol{h}) = \displaystyle \int_{-2H}^{2H} \lambda(\boldsymbol{r})e^{-i\boldsymbol{h} \cdot \boldsymbol{r}} \mathrm{d}z \;\;\;\;\;\;\;\;\; (1)
$$

$${\lambda (\boldsymbol{r})}$$：電子密度（単位長さあたりの電子数）、$${\mathrm{d}z}$$：線要素

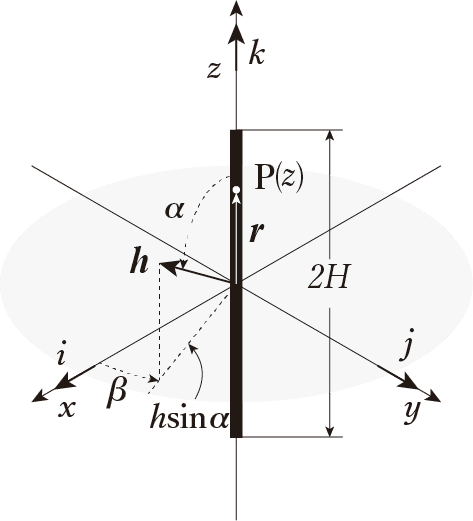
図2のように、散乱ベクトル$${\boldsymbol{h}}$$を極座標で表し、直交座標系の単位ベクトル$${\boldsymbol{i}}$$、$${\boldsymbol{j}}$$、$${\boldsymbol{k}}$$で表現すると、

$$
\boldsymbol{h} = (h \sin \alpha \cos \beta) \boldsymbol{i} + (h \sin \alpha \sin \beta) \boldsymbol{j} + (h \cos \alpha) \boldsymbol{k} \\ \boldsymbol{r} = z\boldsymbol{k}
$$

よって、

$$
\boldsymbol{h} \cdot \boldsymbol{r} = hz\cos \alpha
$$

この結果を式(1)に代入すると、

$$
F(\boldsymbol{h}) = \lambda_0\displaystyle \int_{-H}^H e^{-ihz \cos \alpha} \mathrm{d}z
$$

$$
\displaystyle \int_{-H}^H e^{-ihz \cos \alpha} \mathrm{d}z = \bigg [ \dfrac{e^{-ihz \cos \alpha}}{-ih \cos \alpha} \bigg ]_{-H}^H = \dfrac{2}{h \cos \alpha} \cdot \dfrac{e^{ihH \cos \alpha} - e^{-ihH \cos \alpha}}{2i} = \\ = \dfrac{2 \sin {(hH \cos \alpha)}}{h \cos \alpha}
$$

ここで、正弦関数（sin）の複素数表現を用いました[2]。
　こうして、問1の結果を考慮して、

$$
F(\boldsymbol{h}) = N_e \dfrac{\sin {(hH \cos \alpha)}}{hH \cos \alpha} \;\;\;\;\;\;\;\;\; （答）
$$

構造因子$${F(\boldsymbol{h})}$$は、散乱ベクトル$${\boldsymbol{h}}$$の大きさ$${h}$$だけに依存するのではなく、方角にも依存します。$${\cos \alpha}$$が含まれているからです。

(問3) 散乱強度$${I(\boldsymbol{h})}$$は、次式で与えられます[1]：

$$
I(\boldsymbol{h}) = A_e^2 |F(\boldsymbol{h})|^2
$$

針はランダムに配向します。針を配向させる代わりに、散乱ベクトル$${\boldsymbol{h}}$$の方角をランダムに配向させます。針を動かすか、散乱ベクトルを動かすか、相対的だからどちらでもかまわないからです。こうして、散乱強度（$${I(h)}$$として与えます）は散乱ベクトルのあらゆる方角（$${\alpha, \beta}$$）の平均値として与えられます[3]：

$$
I(h) = \langle I(\boldsymbol{h}) \rangle = \dfrac{A_e^2}{4\pi} \displaystyle \int_{\alpha = 0}^\pi \int_{\beta = 0}^{2\pi} |F(\boldsymbol{h})|^2 \sin \alpha \mathrm{d}\alpha \mathrm{d}\beta = \\ = \dfrac{A_e^2 N_e^2}{4\pi} \displaystyle \int_{\alpha = 0}^\pi \int_{\beta = 0}^{2\pi} \dfrac{\sin^2 {(hH \cos \alpha)}}{(hH \cos \alpha)^2} \sin \alpha \mathrm{d}\alpha \mathrm{d}\beta
$$

被積分関数は$${\beta}$$を含まないから、$${\beta}$$に関する積分は独立に実行できて結果は$${2\pi}$$。最後に、$${\alpha}$$に関する次の積分が残ります：

$$
I(h) = \dfrac{A_e^2 N_e^2}{2}\displaystyle \int_0^\pi \dfrac{\sin^2 {(hH \cos \alpha)}}{(hH \cos \alpha)^2} \sin \alpha \mathrm{d}\alpha　\;\;\;\;\;\;\;\;\; (2)
$$

上式を少し簡単にすることを試みます。$${\alpha' = \pi - \alpha}$$とおくと、

$$
\sin^2 {(hH \cos \alpha)} =\sin ^2{(hH \cos {(\pi - \alpha')})} = \\ =\sin ^2{(-hH \cos \alpha')} = [-\sin {(hH \cos \alpha')}]^2 = \sin ^2{(hH \cos \alpha')}\\ \cos^2 \alpha = \cos^2 {(\pi-\alpha')} = [ -\cos \alpha' ]^2 = \cos ^2 \alpha' \\ \sin \alpha = \sin {(\pi - \alpha')} = \sin \alpha' \\ \mathrm{d}\alpha = - \mathrm{d} \alpha'
$$

だから、

$$
\displaystyle \int_0^\pi (\cdots )\mathrm{d}\alpha = \int_0^{\pi/2} (\cdots )\mathrm{d}\alpha + \int_{\pi/2}^\pi (\cdots )\mathrm{d}\alpha = \\ = \int_0^{\pi/2} (\cdots )\mathrm{d}\alpha + \int_{\pi/2}^0 (\cdots )(-\mathrm{d}\alpha') = \int_0^{\pi/2} (\cdots )\mathrm{d}\alpha + \int_0^{\pi/2} (\cdots )\mathrm{d}\alpha' = \\　＝2 \int_0^{\pi/2} (\cdots )\mathrm{d}\alpha
$$

となります。式(2)は少し簡単になって、

$$
I(h) = A_e^2 N_e^2\displaystyle \int_0^{\pi/2} \dfrac{\sin^2 {(hH \cos \alpha)}}{(hH \cos \alpha)^2} \sin \alpha \mathrm{d}\alpha　\;\;\;\;\;\;\;\;\; (3)
$$

式(3)をさらに変形します。積分変数の変換$${x=hH \cos \alpha}$$を行うと、$${\sin \alpha \mathrm{d} \alpha = -\mathrm{d}x/(hH)}$$となるから、

$$
\displaystyle \int_0^{\pi/2} \dfrac{\sin^2 {(hH \cos \alpha)}}{(hH \cos \alpha)^2} \sin \alpha \mathrm{d}\alpha = \dfrac{1}{hH} \int_0^{hH} \dfrac{\sin^2{x}}{x^2} \mathrm{d}x
$$

ここで、部分積分を行うと[4]、

$$
\displaystyle \int_0^{hH} \dfrac{\sin^2{x}}{x^2} \mathrm{d}x = \bigg [ - \dfrac{\sin^2{x}}{x} \bigg ]_0^{hH} - \int_0^{hH} \Big ( -\dfrac{1}{x} \Big ) 2\sin x \cos x \mathrm{d}x
$$

さらに[5, 6]、

$$
\bigg [ - \dfrac{\sin^2{x}}{x} \bigg ]_0^{hH} = - \dfrac{\sin^2{hH}}{hH} + \displaystyle \lim_{x \to 0}\dfrac{\sin^2 x}{x}
$$

$$
\displaystyle \lim_{x \to 0} \dfrac{\sin^2 x}{x} = \lim_{x \to 0} \big (x - \dfrac{x^3}{3}+ \cdots \big )=0
$$

$$
\displaystyle\int_0^{hH} \Big ( -\dfrac{1}{x} \Big ) 2\sin x \cos x \mathrm{d}x= -\int_0^{hH}\dfrac{\sin {2x}}{x} \mathrm{d}x = -\int_0^{2hH}\dfrac{\sin {x'}}{x'} \mathrm{d}x' = \\ = -\mathrm{Si}(2hH)
$$

最後の$${\mathrm{Si} \; x}$$は積分正弦関数といわれます[7]。結局式(3)は、

$$
I(h) = A_e^2 N_e^2 \bigg [ \dfrac{\mathrm{Si}(2hH)}{hH} - \dfrac{\sin^2{(hH)}}{(hH)^2} \bigg ] \;\;\;\;\;\;\;\;\; （答）
$$

次に$${I(0)}$$を求めます。見やすくするために、$${y=hH}$$とおくと、上式は、

$$
\dfrac{\mathrm{Si}(2y)}{y} - \dfrac{\sin^2 y}{y^2} = \\ = \dfrac{1}{y}\Big (2y - \dfrac{4y^3}{9} + \cdots \Big) - \dfrac{1}{y}\Big (y-\dfrac{y^3}{3} + \cdots \Big ) = 1 - \dfrac{y^2}{9} + \cdots \;\;\;\;\;\;\;\;\; (4)
$$

となります。ここでは、文献[5, 7]のべき級数も使いました。問3の答と式(4)をあわせると、

$$
I(0) = \displaystyle \lim_{h \to 0 (y \to 0)} I(h) = A_e^2 N_e^2
$$

（別法）　式(3)は円柱の散乱強度[8]からも得られます。断面の半径が$${R}$$、高さが$${2H}$$の円柱の散乱強度は、

$$
I(h) = A_e^2 N_e^2\displaystyle \int_0^{\pi/2} \dfrac{4J_1^2(hR \sin \alpha)}{(hR \sin \alpha)^2} \dfrac{\sin^2{(hH \cos \alpha)}}{(hH \cos \alpha)^2} \sin \alpha \mathrm{d} \alpha
$$

ここで、半径$${R \rightarrow 0}$$とすれば円柱が針になります。このとき、被積分関数の第1項は、

$$
\displaystyle \lim_{R \to 0} \dfrac{2 J_1 {(hR \sin \alpha)}}{hR \sin \alpha} = 1
$$

となるから、式(3)が得られます。実際、ベッセル関数$${J_1(z)}$$のべき級数展開は[9]、

$$
J_1(z) = \dfrac{1}{2}z - \dfrac{1}{16}z^3 +\dfrac{1}{384}z^5 - \dfrac{1}{18432}z^7 + \cdots
$$

となるから、

$$
\dfrac{2J_1(x)}{x} =1- \dfrac{1}{8}x^2 + \cdots
$$

となります。これから$${x \rightarrow 0}$$のとき、$${2J_1(x)/x \rightarrow 1}$$となることがわかります。

(問4) $${P(h) = I(h)/I(0)}$$だから、問3より、

$$
P(h) = \dfrac {\mathrm{Si}(2hH)}{hH} - \dfrac{\sin^2{(hH)}}{(hH)^2}
$$

(問5) 式(4)の$${y}$$を$${hH}$$に戻すと、

$$
P(h) = 1 - \dfrac{H^2}{9} h^2 + \cdots \;\;\;\;\;\;\;\;\; (Hh \ll 1)
$$

対数についてのべき級数を使うと[10]、

$$
\ln P(h) = - \dfrac{H^2}{9} h^2 + \cdots
$$

これとGuinierの法則（Guinierプロット）[1]：

$$
\ln P(h) = - \dfrac{R_G^2}{3} h^2 + \cdots \;\;\;\;\;\;\;\;\; (R_Gh \ll 1)
$$

と比べると、

$$
R_G = \dfrac{H}{\sqrt{3}} \;\;\;\;\;\;\;\;\; （答）
$$

が得られます[1]。
（別法）回転半径$${R_G}$$の定義から[1]、

$$
R_G^2 = \dfrac{\displaystyle \int_V\rho (\boldsymbol{r})(\boldsymbol{r}-\boldsymbol{r}_G)^2\mathrm{d}\boldsymbol{r}}{\displaystyle \int_V\rho (\boldsymbol{r})\mathrm{d}\boldsymbol{r}}=\dfrac{\lambda_0\displaystyle \int_{-H}^H z^2 \mathrm{d}z}{\lambda_0\displaystyle \int_{-H}^H \mathrm{d}z} =\dfrac{ \Big[ \dfrac{z^3}{3} \Big ]_{-H}^H}{\Big[z \Big ]_{-H}^H} = \dfrac{\dfrac{2H^3}{3}}{2H} = \dfrac{H^2}{3}
$$

よって、同じ結果が得られ、

$$
R_G = \dfrac{H}{\sqrt{3}}　\;\;\;\;\;\;\;\;\; （答）
$$

なお、ここでは針の重心は図2の原点にあるとしたので、$${\boldsymbol{r}_G = \boldsymbol{0}}$$となります。
　参考までに、図3に針の散乱関数を示します。

図3 簡単な形状の散乱関数P(h)．横軸は波数ベクトルで、回転半径RGで規格化されています。針（Needle）は最も緩く減衰します。Pythonで計算しました。

（終）

文献

[1] 小角X線散乱（SAXS）（1） - 基本的なこと（note記事）
[2] $${\sin z = (e^{iz} - e^{-iz})/2i }$$
[3] 方角に依存する関数$${f(\theta, \varphi)}$$の平均$${\langle f \rangle}$$は、極座標では次式で与えられる：

$$
\langle f \rangle = \dfrac{1}{4\pi}\displaystyle \int_{\varphi=0}^{2\pi} \int_{\theta=0}^\pi f(\theta, \varphi) \sin\theta \mathrm{d}\theta \mathrm{d}\varphi
$$

$${\sin\theta \mathrm{d}\theta \mathrm{d}\varphi}$$は微小立体角を極座標で表したものです。
[4] 部分積分、

$$
\displaystyle \int f(x)g'(x) \mathrm{d}x = f(x)g(x) - \int f'(x)g(x) \mathrm{d}x
$$

ここでは、$${f(x)=\sin^2{x}}$$、$${g(x)=-1/x}$$とおいています。
[5] べき級数展開を利用します。その前に、三角関数の性質から、$${\sin^2 x = (1-\cos {2x})/2}$$とします。$${\cos x}$$に対して次のべき級数ができます：

$$
\cos x = \displaystyle \sum_{n=0}^\infty (-1)^n \displaystyle \frac{x^{2n}}{(2n)!} = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} +- \cdots \;\;\;\;\;\; [|x|<\infty]
$$

$${x \ll 1}$$で、

$$
\dfrac{\sin^2 x}{x} = \dfrac{1-\cos {2x}}{2x} = \dfrac{1}{2x} \Big [ 1 - \big (1 - \dfrac{4x^2}{2!} + \dfrac{16x^4}{4!} + \cdots \big ) \Big ] = \\ =x - \dfrac{x^3}{3}+ \cdots
$$

[6] 森口繁一、宇田川銈久、一松信、数学公式Ⅱ（岩波全書）、岩波書店、1957.
[7] 森口繁一、宇田川銈久、一松信、数学公式Ⅲ（岩波全書）、岩波書店、1960. 積分正弦関数：

$$
\mathrm{Si}\;x = \displaystyle \int_0^x \dfrac{\sin t}{t} \mathrm{d}t = \\ =
\displaystyle \sum_{n=0}^\infty \dfrac{(-1)^n x^{2n+1}}{(2n+1)!(2n+1)} = x - \dfrac{x^3}{18} + \dfrac{x^5}{600} - \cdots
$$

[8] 小角X線散乱（SAXS）（13） - 【演習】円柱の散乱関数（note記事）.
[9] ベッセル関数の定義[7]：

$$
J_\nu(z) = \left( \dfrac{z}{2} \right) \displaystyle \sum_{n=0}^\infty \dfrac{(-1)^{n}(z/2)^{2n}}{n!\varGamma(\nu + n + 1)}
$$

ここで、$${\varGamma(z)}$$はガンマ関数[7]。例えば、$${\varGamma(n+1)=n!}$$です。

[10] $${hH \ll 1}$$のとき、次のべき級数展開が使えます[6]：$${x=hH}$$として、

$$
\ln{(1-x)} = -\displaystyle \sum_{n=1}^\infty \frac{x^n}{n} = -x-\frac{x^2}{2}-\frac{x^3}{3}+- \cdots \; [|x|\leq 1, \; x\neq 1]
$$

様々な形状の散乱関数（形状因子、干渉因子）

【免責事項】本記事は単なるメモとして書かれたもので、その正確性を必ずしも保証するものではありません。本記事によって生じたトラブル、損失、又は損害に対して一切責任を負いません。また、著者が所属する組織とは関係ありません。誤りがあればご指摘ください。クレームはご遠慮ください。

この記事が気に入ったらサポートをしてみませんか？